Закрепление изученного материала

Задание 8 (с. 35)

а) Можно ответить на вопрос, сделав определенные вычисления:

х = 30 000; 50 000 - 30 000 = 20 000; или в результате рассуждений: сумма (х + 20 000) — это число х да еще число 20 000; тогда число х — это сумма (х+ 20 000) без числа 20000; значит, число х меньше суммы (х + 20 000) на 20 000;

б) х = 12 800; делимое больше чем частное на 9600 (12 800-3200=9600).

Задание 7 (с. 35)

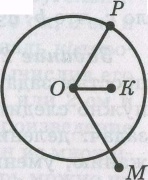
ОР = 20 мм; ОК < 20 мм; ОМ > 20 мм; ОК<ОР< ОМ.

Задание 10 (с. 35)

I —18с.

II —?, на 10 с. больше

Ответ: повесть занимает 46 страниц.

Задание 6 (с. 35) – самостоятельно по вариантам

Подведение итогов урока

МАТЕМАТИКА

Тема: Смысл действия деления

Цели: обобщить знания по раскрытию конкретного смысла действия деления на примере задач; решать задачи на движение.

Организационный момент

Устный счёт

Решите уравнения:

х - 60 = 9

800: х = 40

х·50 = 2 500

х·70 = 2 100

Решите задачи:

а) Из двух городов навстречу друг другу выехали одновременно мотоциклист и велосипедист. Мотоциклист ехал со скоростью 48 км/ч, а велосипедист — 12 км/ч. Они встретились через 5 ч. Какое расстояние проехали мотоциклист и велосипедист?

б) Из двух городов, расстояние между которыми 240 км, навстречу друг другу выехали одновременно мотоциклист со скоростью 46 км/ч и велосипедист со скоростью 14 км/ч. Через какое время они встретятся?

Задание 6*. Нужно установить соответствие между тремя девочками (Таня, Ира, Лена) и тремя местами (I, II, III) с учетом условий:

	I	II	III
Таня	-	+	-
Ира	-	-	+
Лена	+	-	-

1) место Иры нечетное;

2) Таня заняла не первое место;

3) место у Лены выше, чем у Иры.

Из 1) и 3) следует, что у Иры III место. Остались места I и П.

Из 2) следует, что у Тани II место. Тогда I место у Лены.

Сообщение темы и целей урока

Объяснение нового материала

Задание 1 (с. 36)

Ученики составляют выражения к задачам: а) а: 8; б) 36: с; в) k • т. Можно дать значения буквам, сделать вычисления, составить и решить обратные задачи. В результате дети убеждаются во взаимосвязи умножения и деления: найти частное от деления числа а на число в означает найти такое число с, что в • с = а.

Задание 2 (с. 36)

По выражению 42: 7 дети составляют простые задачи с разным содержанием. Но при этом нужно следить, чтобы прозвучали все виды простых задач: деление на равные части, деление по содержанию, уменьшение числа в несколько раз, кратное сравнение.

Закрепление изученного материала

Задание 3 (с. 36) - самостоятельно

Задание 5 (с. 37)

¾ Что означает «обратный путь"? Сколько это километров? На какой путь лодка затратила меньше времени? Почему? Почему скорость лодки по течению всегда больше, чем скорость против течения?

	Скорость	Время	Расстояние
Против течения	24 км/ч	?	72 км
По течению	?	?, на 1 ч меньше	72 км

Ответ: 36 километров в час.

Задание 8 (. 37)

Сначала нужно нарисовать прямоугольник с площадью 20 см². Таких прямоугольников может быть три: с размерами 1 см и 20 см; 2 см и 10 см; 4 см и 5 см. Прямоугольник, площадь которого в 2 раза меньше, можно нарисовать, вычислив его размеры по площади 10 см²: 1 см и 10 см или 2 см и 5 см. А можно рассуждать так: чтобы произведение (площадь) уменьшить в 2 раза, нужно один из множителей (сторону) уменьшить в 2 раза. Теперь можно из трех первых прямоугольников образовать новые.

10 см 10 см

Задание 7 (с. 37)

Задание 4 (с. 36)

Подведение итогов урока

6. Домашнее задание: № 9, № 10 (ст. 1,2), с. 37

МАТЕМАТИКА

Тема: Частные случаи деления.

Цели: обобщить знания учеников о частных случаях деления; складывать и решать уравнения.

Организационный момент

Устный счёт

Решите примеры

2000-75: 15- 100

1 000 + 72: 18 • 60

560: 140•1 000 - 2000

(98: 14) • (96: 12)

65: 13•200 + 3200

1 000-48: 16•300

Задание 6 (с. 39)

При одинаковых числовых значениях получаются разные уравнения:

а) х•8 = 64; в) х-8 = 64;

б) х: 8 = 64; г) х - 64 = 8.

Задание 2 (с. 38)

Решите задачи

Заполните таблицу:

Скорость, км/ч	Время, ч	Расстояние, км
		?
		?
	?
	?
?
?		1 000

• Ель живет до 1 200 лет, а сосна — до 600 лет. Во сколько раз ель живет дольше, чем сосна? На сколько лет ель живет меньше, чем сосна?

• Дятел за день съедает 900 короедов, а мухоловка-пеструшка — 300 мух и комаров. Во сколько раз меньше уничтожает вредителей мухоловка, чем дятел? Сколько вредителей леса уничтожают за день дятел и мухоловка вместе?

Задание 5* (с. 39)

Через 25 с первый муравей будет в точке Т, второй — в точке О.

Способ I.

1) 1•25 = 25 (см) — проползет первый муравей;

2) 2 • 25 = 50 (см) — проползет второй муравей;

3) 25 + 50 = 75 (см) — расстояние между муравьями.

Способ II.

1) 1 + 2 = 3 (м/с) — скорость отдаления муравьев;

2) 3 • 25 = 75 (см) — расстояние между муравьями.

Расстоянием между муравьями можно считать и ту часть периметра, которую муравьи не пробежали. 5 + 30 + 10 = 45 (см) или 120 - 75 = 45 (см).

⇐ Предыдущая 24 25 26 27 282930 31 32 33 Следующая ⇒

Воспользуйтесь поиском по сайту: