Процентными и учетными ставками

Обозначение	Формулы взаимосвязи ставок (начало)
q	i	j
q	Простая процентная ставка
i		Сложная процентная ставка
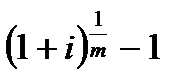
j			Годовая номинальная процентная ставка
f
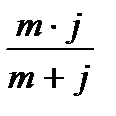
c
d
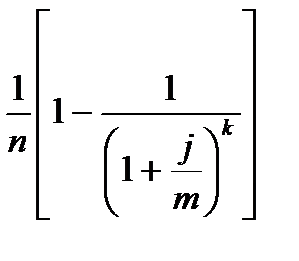
n – число годовых периодов начислений;
m – число месячных периодов начислений;
k =n∙m – общее количество периодов начислений.

q - Простая процентная ставка

i - Сложная процентная ставка

j - Годовая номинальная процентная ставка

f - Годовая номинальная учетная ставка

с - Сложная учетная ставка

d - Простая учетная ставка

Процентные и учетные ставки решают одинаковые задачи: устанавливают: доходность при операции наращения и размеры дисконтированных сумм при учетных операциях. Возможен выбор таких процентных или учетных ставок, при использовании которых финансовые последствия будут равноценными. Ставки, обеспечивающие равноценность финансовых послед­ствий, называются эквивалентными или релятивными (относи­тельными). Эквивалентность определяется для двух вари­антов: когда временные базы (К – число дней в году) равны и когда они различны. Для каждого периода наращения рассчитывается своя эквивалентная ставка.

Таблица 4.1 (окончание).

Соотношения между различными

Процентными и учетными ставками

 

Таблица 4.1 (окончание).

Соотношения между различными

Процентными и учетными ставками

Обозначение	Формулы взаимосвязи ставок (окончание)
f	c	d
q
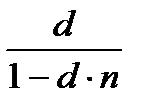
i
j
f	Годовая номинальная учетная ставка
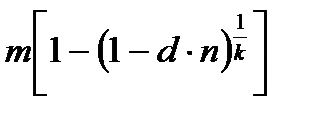
c		Сложная учетная ставка
d			Простая учетная ставка
n – срок ссуды или кредита в годах;
m – число платежей в течении года;
k =n∙m – общее количество периодов начислений.

Различают три метода процентных расчётов, которые зависят от выбранного периода начисления.

1. Точные проценты с точным числом дней ссуды («англий­ская практика»). При этом методе определяется фактическое число дней (t) между двумя датами (датой получения и погашения креди­та), продолжительность года принимается равной К= 365 (366) дней.

2. Обыкновенные проценты с точным числом дней ссуды («фран­цузская практика»); величина t рассчитывается, как и в преды­дущем случае.

3. Обыкновенные проценты с приближенным числом дней ссуды («германская практика»); величина t определяется коли­чеством месяцев по 30 дней в каждом начиная с момента выда­чи ссуды и до момента ее погашения и точным числом дней ссуды в неполном месяце; продолжительность года К= 360 дней.

При точном и приближенном методах начисления процентов день выдачи и день погашения ссуды принимаются за 1 день.

Замена одного вида ставки на другой при соблюдении принципа эквивалентности не изменяет финансовых отношений сторон в рамках одной операции. Для участвующих в сделках сторон обычно безразлично, какой вид ставки представлен в контракте. Формулы эквивалентности ставок, представленные в табл. 4.1, получены из равенства попарно взятых множителей наращения.

При обосновании и выборе инвестиционных решений большое значение имеет непрерывное наращение. С помощью непрерывных процентов можно учесть сложные закономерности процесса наращения, например, использовать изменяющиеся по определённому закону процентные ставки.

При непрерывном наращении процентов применяют особый вид процентной ставки – силу роста (force of interest). Сила роста характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени. Она может быть постоянной или изменяться во времени. Можно также установить эквивалентность дисконтного множителя и силы роста непрерывных процентов, что выражается следующей формулой:

= = .

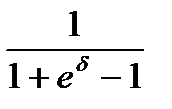⇐ Предыдущая12131415161718192021Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: