 |
Инвестиционный кредит и дисконтирование
|
|
|
|
Инвестиционный кредит в условиях рынка выступает в различных формах. Основными являются коммерческий и банковский кредит.
Коммерческий кредит есть предоставление инвестиционных услуг одним субъектом сделки другому с оплатой через определенное время, т.е. происходит отсрочка уплаты денег за инвестиционные услуги. Распространенным инструментом этого кредита является коммерческий вексель.
Вексель — это особый вид письменного долгового обязательства, дающий его владельцу бесспорное право требовать по истечении указанного в нем срока уплаты денег с должника. Векселя могут быть простыми и переводными. Простой вексель представляет собой долговое обязательство, выдаваемое заемщиком на имя кредитора, и содержит указание места и времени выдачи долгового обязательства, его суммы, места и времени платежа и наименование лица, которому заемщик обязан произвести платеж.
Переводной вексель, или тратта, представляет собой письменный приказ одного лица (кредитора) другому лицу (заемщику) об уплате суммы, обозначенной в векселе, третьему лицу.
Банковский кредит — это кредит, предоставляемый одним субъектом сделки другому в виде денежной ссуды. Механизм оформления банковских ссуд предусматривает различные варианты, в том числе выписку ссудозаемщиком векселей на имя кредитора.
Векселедержатель (кредитор) или владелец иных долговых обязательств в случае необходимости получения денег по векселю или другим долговым обязательствам ранее указанных в них сроков может продать его банку или другому субъекту по пониженной цене, т.е. по цене ниже номинальной стоимости векселя, указанной в нем. Такая сделка носит название учета векселя, или дисконтирования. Сумма, полученная владельцем векселя в результате этой сделки, называется дисконтированной величиной. Она ниже номинальной стоимости векселя на величину процентного платежа, вычисленного со дня дисконтирования до дня, ранее предусмотренного для погашения векселя. Дисконтом называется разность между номинальной стоимостью долгового обязательства и суммой, полученной векселедержателем в результате учета векселя.
|
|
|
Дисконтирование векселя является, по существу, формой кредитования векселедержателя путем досрочной выплаты ему обозначенной в векселе суммы за вычетом определенных процентов. Для субъекта сделки, принявшего к учету вексель, дисконт является доходом. Дисконт рассчитывается на основе так называемой учетной ставки, величина которой зависит от срока, остающегося до оплаты обязательства, и существующих банковских процентных ставок. Учетные ставки также рассчитываются в процентах.
Термин «дисконтирование» употребляется в финансовом менеджменте весьма широко. Под этим термином может пониматься способ нахождения величины P на некоторый момент времени при условии, что в будущем при начислении на нее процентов она могла бы составить наращенную сумму S.
Величину P, найденную дисконтированием наращенной величины S, называют текущей современной, или приведенной, величиной. С помощью дисконтирования в финансовых вычислениях учитывается фактор времени.
Например, если сегодня инвестируется 10,0 млн. руб., рассчитывая получить 10% дохода, то через год стоимость ваших инвестиций составит 11,0 млн. руб. — это будущая стоимость вашей инвестиции, а текущая стоимость составляет 10,0 млн. руб.
При математическом дисконтировании решается задача, обратная определению наращенной суммы. Сформулируем ее следующим образом: какую сумму следует выдать в долг на n лет, чтобы при начислении на нее процентов по ставке i получить наращенную сумму, равную S?
|
|
|
Для отражения этой задачи используем формулу наращения по простой ставке процентов получим:
P = S ∙ 
,
где 
- дисконтный множитель, показывающий, во сколько раз первоначальная сумма ссуды меньше наращенной. Преобразуем данное выражение, получим:
D = S – P = P ∙n ∙ i.
Эта разность называется дисконтом. Его следует отличать от дивизора (множителя D* = 
), в отличие от которого он характеризует фактический натуральный стоимостной прирост.
Математический метод дисконтирования может применяться с использованием не только простой, но и сложных ставок.
Для этого из выражения S = P (1+ i)n найдем значение P для сложной процентной ставки:
P = S ∙ 
= S ∙ (1+ i)-n,
где = (1+ i)-n – дисконтный (учётный) множитель. Значения этого множителя обычно представляются в табулированном виде в специальных справочниках по финансовым вычислениям.
При начислении процентов т раз в году получим следующее выражение: P = S ∙ 
= S ∙ 
, где = 
-дисконтный множитель.
Как указывалось выше, разность S – P = D является дисконтом, поэтому можно записать:
D = S – S ∙ = S 
.
Приведенная величина P представляет приведенную величину (современную – present value - по англ.). Одним из её свойств является то, что величина процентной ставки, по которой производится дисконтирование, и её современная (приведенная) величина находятся в обратной зависимости, иначе, чем выше процентная ставка, тем меньше современная величина при прочих равных условиях. В такой же обратной зависимости находятся современная величина и срок платежа. С увеличением срока платежа n современная величина будет уменьшаться.
В учетных (дисконтных) операциях, помимо сложной процентной ставки, широко применяется сложная учетная ставка. В этом случае дисконтирование осуществляется по формуле:
P = S ∙ (1 - с)n,
где с – сложная годовая учетная ставка. Дисконт в этом случае определится как разность:
D = S – P = S – S ∙ (1 - с)n = S ∙ [ 1 – (1 - с)n].
Зная величины S, P и n можно определить значение сложной учетной ставки (с):
S = 
, откуда с = 1 - 
.
Различие в величине дисконтных множителей при использовании простой (d) и сложной (с) учётных ставок, равных по своей величине, будет зависеть от срока ссуды. При дисконтировании m раз в году используется номинальная учетная ставка.
|
|
|
Расчёт дисконтированной величины при номинальной учетной ставке производится по формуле:
Р = S ∙ 
,
где f – номинальная учетная ставка;
а k = m∙n – общее число периодов дисконтирования.
При дисконтировании m раз в году вводится понятие эффективной ставки, под которой имеется ввиду сложная годовая учётная ставка, эквивалентная номинальной учётной ставке при заданном значении m.
Эффективная процентная ставка – ставка, отражающая реальный доход от коммерческой сделки, иначе, ставка, по которой фактически были начислены проценты на первоначальную сумму.
Из приведенных выше определений эффективной ставки можно записать:
= 
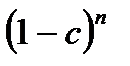или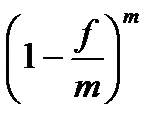 
= 
,
тогда c = 1 - 
.
Отсюда можно сделать вывод, что эффективная учётная ставка (c) меньше номинальной учётной ставки (f).
Величина номинальной учетной ставки f при дисконтировании m раз в году определится так:
f = 
.
Сроки ссуды при дисконтированной сложной годовой ставке и номинальной учетной ставке m раз в году составят:
| при сложной годовой ставке | при номинальной учётной ставке |
n =  ;
| n =  .
|
Для расчета наращенных сумм и дисконтирования были использованы различные виды ставок q, i, j, f, c, d. Использование в финансовой сделке различных видов ставок, при равных условиях, приводит к различным финансовым результатам. Так как результаты финансовых сделок зависят от числа периодов начисления процентов.
При равенстве ставок q = i = j = f = c = d множители наращения будут представлять следующий мажорантный ряд:
| при n < 1 | (1 + i) n | < | (1 + n∙q) | < | (1 - n∙c)-1 | < | (1 - c)-n |
| при n > 1 | (1 + n∙q) | < | (1 + i) n | < | (1 - c)-n | < | (1 - n∙d) |
| при n = 1 | (1 + n∙q) | = | (1 + i) n | < | (1 - n∙d) | = | (1 - c)n |
Система неравенств для дисконтных множителей будет иметь вид:
| при n < 1 | (1 - c)n | < | (1 - n∙d) | < | (1 + n∙q)-1 | < | (1 + i)- n |
| при n > 1 | (1 - n∙d) | < | (1 - c)n | < | (1 + i)- n | < | (1 + n∙q)-1 |
| при n = 1 | (1 - n∙d) | = | (1 - c)n | < | (1 + n∙q)-1 | = | (1 + i)- n |
Эти соотношения между множителями наращения, а также дисконтными множителями используются в финансовом менеджменте для выбора стратегии, которой следует руководствоваться банкам и коммерческим структурам при формировании инвестиционной политики.
|
|
|
Финансовые последствия при использовании номинальных ставок j и f зависят от принятого значения величины m, которое может варьироваться в широком диапазоне.
Финансовые ренты и потоки
Ранее рассматривались случаи, когда начисление процентов или дисконтирование производилось по отношению к одноразовому вкладу (депозиту) или ссуде. Погашение среднесрочной и долгосрочной банковских задолженностей, коммерческого кредита, инвестирование средств в различные программы, создание денежных фондов целевого назначения и другие платежи в большинстве случаев предусматривают выплаты, производимые через определенные промежутки времени. При этом возникает ряд последовательных платежей, которые обычно именуют потоком платежей.
Ряд последовательных фиксированных платежей, производимых через равные промежутки времени, называется финансовой рентой, или аннуитетом. Финансовая рента (далее — рента) может быть охарактеризована рядом параметров, важнейшими из которых являются:
член ренты — величина каждого отдельного платежа;
период ренты — временной интервал между двумя платежами;
срок ренты — время от начала реализации ренты до момента начисления последнего платежа;
процентная ставка — ставка, используемая для расчета наращения или дисконтирования платежей, составляющих ренту.
Кроме перечисленных параметров рента характеризуется: количеством платежей в течение года; частотой начисления процентов (т.е. количеством периодов в году, когда начисляются проценты); моментом производства платежей (в начале, середине или в конце года) и другими.
|
|
|
