Аналогично для простой и сложной учетных ставок может быть установлена эквивалентность силы роста и учетных ставок.

Таким образом, дискретные и непрерывные ставки наращения находятся в функциональной зависимости друг от друга. Основной проблемой выбора ставки среди возможных вариантов финансирования является критерий отбора, который устанавливается из условий самого инвестиционного проекта.

 

Расчёты по залоговым операциям

Залоговые операции представляют собой краткосрочный кредит под залог легкореализуемого движимого имущества. Одной из форм залоговых операций является ломбардный кредит. Такой кре­дит может осуществляться и в форме банковского кредита под залог де­понируемых в банке ценных бумаг. В этом случае в залог принимаются ценные бумаги, котирующиеся на фондовой бирже или имеющие органи­зованный свободный рынок. Сумма кредита составляет от 50 до 90% их курсовой стоимости. Срок кредита, как правило, не пре­вышает трех месяцев.

Контракт на получение ломбардного кредита может преду­сматривать различные условия выплаты долга. Так, заемщик может:

· погасить весь долг единовременным платежом в срок, пре­дусмотренный контрактом;

· выплатить в срок лишь часть долга, а оставшуюся часть погашать в следующем перио­де;

· продлить срок погашения на следующие три месяца.

При расчетах учитывается точное количество дней в месяце, а про­должительность года принимается равной 360 дням.

В случае если заемщик не погасит кредит вовремя, он обязан рассчитаться с кредитором по увеличенной (штрафной) процент­ной ставке за весь период просрочки платежа. Если кредит все же не будет погашен, право собственности переходит к креди­тору, который реализует имущество и удерживает из выручки сумму долга вместе с начисленными процентами.

Рассмотрим пример расчета при использовании ломбард­ного кредита.

Банк предоставил клиенту (предприятию) кредит на 3 месяца с 15.05 по 15.08 под залог 200 акций, курсовая стоимость которых в день выдачи кредита (15.05) составляла по 25 тыс. руб. за акцию. Сумма кредита оценена в 60% курсовой стоимости залога. Кредит выдается под 12,5% (i = 12,5) годовых.

За обслуживание долга банк взимает 1,0% от номи­нальной суммы кредита.

Определим фактический размер кредита, полученного клиентом банка.

Курсовая стоимость залога: 200 ∙ 25 тыс. руб. = 5000 тыс. руб. (5,0 млн. рублей). Номинальная величина кредита:
P = 5,0 ∙ 0,60 = 3,0 млн. руб.

Сумма процентных платежей за кредит (с 15.05 по 15.08, где t = 92 дня):

= = = = = 0,0958 млн. рублей.

Затраты банка по обслуживанию долга составляли: 3,0∙0,01= 0,03 млн. рублей (30 тыс. рублей). Сумма кредита, полученная клиентом составляла:

3,0 – (0,0958 + 0,03) = 2,874 млн. рублей.

Потребительский кредит

Потребительский кредит предоставляется банка­ми, финансовыми компаниями или торговыми фирмами для приобретения потребительских товаров. Существуют различ­ные формы потребительского кредита, отличающиеся друг от друга методами и сроками его погашения. Так, например, по­требительский кредит может быть предоставлен с отсрочкой платежа и последующим разовым погашением всей суммы. Другой метод предусматривает погашение платежа в рассрочку — частями. Здесь проценты начисляются на всю сумму кредита, а сумма задолженности (сумма, предоставленная в кредит, плюс начис­ленные проценты) равномерно погашается на протяжении все­го срока кредита.

Разновидностью погашения потребительского кредита в рас­срочку является метод, при котором суммы процентных плате­жей и суммы погашения основного долга изменяются от периода к периоду, по мере изменения сроков погашения ссуды. При этом решается задача определения срока задолженности на лю­бой момент срока погашения кредита. Наиболее распространены методы погашения потребительского кредита равными частями и изменяющимися суммами. Остановимся на них подробнее.

Погашение потребительского кредита равными частями. При погашении потребительского кредита равными частями наращенная сумма долга (S) определяется по уже известной формуле:

S = P (1 + n∙i),

а сумма разового погашающего платежа будет зависеть от числа погашающих платежей в году (m). Тогда сумма разового погасительного платежа равна:

q =

где q - сумма погасительного платежа; n - срок кредита в годах; m - число погасительных платежей в году. Так как проценты начисляются на всю сумму первоначаль­ного долга в течение всего срока погашения, то, несмотря на уменьшение величины долга с каждым платежом, фактическая процентная ставка оказывается значительно выше ставки, пре­дусмотренной при заключении сделки.

Погашение потребительского кредита изменяющимися суммами. При погашении кредита изменяющимися суммами решаются две задачи: определения суммы, идущей на погашение основного долга, и суммы процентных платежей.

Для решения этого вопроса можно воспользоваться «прави­лом 78». Название этого правила вызвано тем, что сумма поряд­ковых номеров месяцев года равна 78 (1 + 2 + 3 +... + 12 = 78). В соответствии с этим правилом уплата процентов при первом платеже составит общей начисленной суммы процентов, а ос­тавшаяся часть платежа пойдет на уплату основного долга. При втором платеже на оплату процентов пойдет 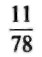общей начи­сленной суммы процентов и т.д. Иначе говоря, процентные платежи являются убывающей арифметической прогрессией, сумма членов которой определя­ется по формуле:

S_n = или S_n = ,

где а₁ - первый член прогрессии;

а_п - последний член;

n - число членов;

d - разность членов прогрессии.

При выдаче ссуды на п лет из условия т погасительных пла­тежей в году последовательные номера месяцев за весь период погашения могут быть записаны в обратном порядке следующим образом:

t₁ = n∙m; t₂ = m∙n – 1; t₃ = m∙n – 2; … t_n = 1.

Сумма этих чисел (Q) по формуле арифметической прогрессии будет равна:

Q = = = .

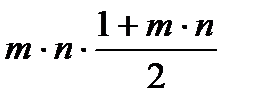В каждом платеже доля порядкового числа данного месяца составит . Абсолютная величина процентного платежа в каж­дом платежном периоде будет равна: ; (при I = P ∙ n ∙ t), где I - сумма всех процентных платежей; P - первоначальная сумма долга; i -процентная ставка, выраженная десятичной дробью. Сумма погашенного долга (U_k) на конец периода К (или момент k) равна:

U_k = Y_k - ,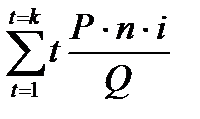

где Y_k - оставшаяся часть непогашенного долга на момент k .

Воспользуемся спосо­бом, когда процентный платеж рассчитывается методом начислений с уменьшением остатка долга. При этом процентный платеж за пользование потребитель­ским кредитом начисляется предварительно: для первого меся­ца (периода) процентный платеж рассчитывается на всю вели­чину долга, а в каждый следующий месяц — на оставшуюся часть долга, т.е. на величину долга, уменьшенную на уже выплачен­ную часть, а сам же долг выплачивается равными долями. Предположим, что величина кредита равна Р и он должен выплачиваться равными месячными платежами т раз с начис­лением процентов по годовой ставке i.

Тогда процентный платёж для первого месяца составит:

I₁ = ;

во втором месяце он составит:

I₂ = = ;

в третьем месяце он составит:

I₃ = = ;

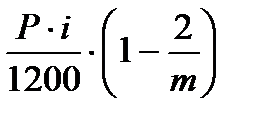в месяце m он составит:

I_m = = = ;

Для определения общей величины процентных выплат за предоставленный кредит просуммируем их месячные значения и обобщив их получим:

I = = ∙ , где - процентный коэффициент.

При ежемесячной выплате кредита равными долями её величина будет равна: q = .

Рассмотрим пример. Предприятие купило в кредит автомобиль стоимостью 452,0 тыс. рублей (Р = 451,2 тыс. руб.) под 18% (i = 18) годовых. Погашение задолженности производится ежемесячными платежами в течение года (m = 12). Составим план погашения (амортизации кредита) с уменьшением остатка долга.

Ежемесячная выплата основного долга:

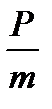= = 37600 руб.

План погашения кредита показан в табл.4.2.

Ежемесячные процентные платежи будут уменьшаться. Общая сумма процентных платежей составит:

I = ∙ = = 43992 руб.

Средняя величина ежемесячных взносов составит:

q = 41266 руб.

Таблица 4.2.

План погашения кредита

Месяц	Непогашенная сумма основного долга, тыс. руб.	Процентный платёж	Месяч-ная оплата долга, тыс. руб.	Сумма месячно-го погаше-ния, тыс. руб.
доля	тыс. руб.
		0,91667	х	х	х
		0,83333
		0,75000
		0,66667
		0,58333
		0,50000
		0,41667
		0,33333
		0,25000
		0,16667
		0,08333
		0,00000
		0,91667
Итого:

⇐ Предыдущая13141516171819202122Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: