 |
Создадим имитирующий портфель безрискового заимствования (ссуды), увязанный с изменением базового актива, для создания денежного потока.
|
|
|
|
Портфель-имитатор для колл-опциона с ценой исполнения X включает заимствование В (долл.) и приобретение h акций базового актива. Его стоимость в момент 0 равна (hS +B), а величина h называется коэффициентом хеджирования или дельтой (Δ). Стоимость портфеля в момент 1 будет равна либо (hSu + RB), либо (nSd +RB). Основным условием решения является выбор таких величин h и В, чтобы стоимость портфеля в момент 1 была бы равной выплате по колл-опциону:
hSu + RB = Cu и nSd +RB = Cd,
где Cu – стоимость колл-опциона, если цена акции равна Su;
Cd – стоимость колл-опциона, если цена акции равна Sd.
Решая систему уравнений, получаем:
h =  ≥ 0 и B =
≥ 0 и B =  .
.
В биноминальном процессе со многими периодами оценка стоимости опциона должна начинаться с заключительного временного периода и идти назад по времени к текущему моменту (нулевому моменту). Портфели, имитирующие (воспроизводящие) опцион, оцениваются на каждом шаге, что и позволяет выявить стоимость опциона на всех шагах. Заключительный шаг биноминальной модели оценки опциона устанавливает стоимость опциона в единицах имитирующего портфеля, составленного из h акций (Δ акций или дельты опциона) базового актива и безрискового заимствования или ссуды.
Пример. Необходимо оценить колл-опцион с ценой базового актива равной $160 за акцию (S= $600). Изменение цены происходит в соответствии с биноминальным процессом: цена от любого своего значения S может либо возрастать до S×1,5, либо уменьшаться до S×0,5. Ставка непрерывного начисления процентов за период составляет r = 18,232% (r = 0.18232). Оценим Европейский колл-опцион на эту акцию с ценой исполнения в $150 и тремя периодами до окончания срока действия. Изменение цены акции и результат расчета стоимости опциона показаны на рис. 5.2.
|
|
|

Рис. 5.2.
Используемые параметры: S = $160; X = $150; n = 3; u = 1,5; d = 0,5; R = er = 1,2; r = 18,232% или 0,18232; p = 0,7; 1-p = 0,3; h см. табл.5.3.
Как указывалось в условии примера, цена акции биноминально может возрастать, либо уменьшаться в стоимости:
S → Su → Suu → Suuu или $160 → $240 → $360 → $540;
S → Sd → Sdd → Sddd или $160 → $80 → $40 → $20,
а стоимости колл-опциона:
С → Сu → Сuu → Сuuu или $85,069 → $141,458 → $235 → $390,
И иметь промежуточные значения.
Расчет стоимости европейского колл-опциона ведётся по формуле:
С = hS ± B = 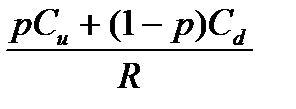 = 0,82031 × $160 - 46,1806 =
= 0,82031 × $160 - 46,1806 =
=  =
=
=  =
=  = 85,069.
= 85,069.
Оценка отдельных значений стоимости колл-опциона производится посредством процедуры обратной индукции. Стоимости конечных значений колл-опциона определяются следующим образом:
Сuuu = Suuu – Х = 540 – 150 = 390;
Сuud = Suud – Х = 180 – 150 = 30;
Сudd = Sudd – Х = 60 – 150 => 0;
Сddd = Sddd – Х = 20 – 150 => 0.
Далее используя логику расчёта стоимости колл-опциона для С, определяются и остальные значения.
Расчет производится так:
Сuu = 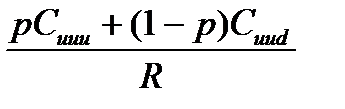 =
=  =
= 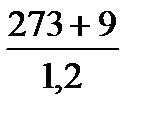 = 235;
= 235;
Сud = 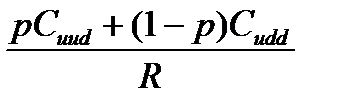 =
=  =
=  = 17,5;
= 17,5;
Сu =  =
=  =
=  = 141,458;
= 141,458;
Сd =  =
= 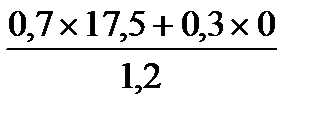 =
=  = 10,208.
= 10,208.
Далее, для проведения более детального анализа, рассчитываются вероятности (они могут рассчитываться и на начальной стадии) и значения дельты (h = Δ):
р =  , h =
, h =  .
.
Данные расчета вероятностей и значений дельта приведены на рис. 5.3.

Рис. 5.3
Более сложной для восприятия, но вместе с тем очень широко употребляемой в инвестиционной отрасли, является оценка стоимости опциона по формуле Блэка-Шоулза. Очевидно, что установление цены венчурного проекта будет зависеть не только от внутреннего состояния, но и от внешней среды. В связи с этим реальное значение цены опциона может изменяться непрерывно. Это особенно свойственно акциям и облигациям, цена которых меняется непрерывно даже в течение одного биржевого дня.
Именно в этом случае для определения стоимости опциона с исполнением в конце периода используют формулу Блэка-Шоулза.
|
|
|
Формула Блэка-Шоулза.
Стоимость европейского колл-опциона определяется по формуле:
C(t) = S×F(d1)- Xe-rt×F(d2),
где d1 =  и d2 = d1 -
и d2 = d1 - 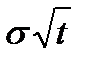
где S - цена базового актива в текущий момент;
X - цена исполнения опциона;
σ - стандартное отклонение цены базового актива;
t – периоды (время) исполнения опциона относительно текущего момента;
r - безрисковая ставка доходности (например, банковская);
F(d) - кумулятивная (интегральная) функция нормального распределения.
Пример (источник [Дамодаран]). 26 марта акции Cisco Systems продавались по цене $13,62 (S = $13,62), а 6 июле того же года акции продавались с ценой исполнения $15 (X=$15). Оценить правильность установления размера колл-опциона, если другие параметры составляли:
срок жизни опциона (6 + 30 +31 + 30 + 6 = 103) = 103/365 = 0,2822;
безрисковая ставка = 4,63 (r = 0,0463);
стандартное отклонение σ = 81% (σ = 0,81).
Подставив данные значения в модель, получим:
d1 = 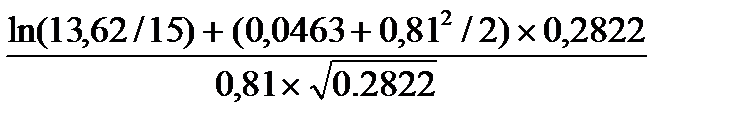 =
=  =
=
=  =
= 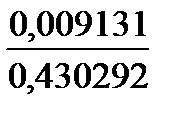 = 0,0212,
= 0,0212,
d2 = d1 - 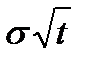 = 0,0212 – 0,81×
= 0,0212 – 0,81×  =
=
= 0,0212 – 0,430292 = - 0,4091.
В электронной таблице Exсel найдем значения функции нормального распределения F1( 0,0212 ) и F2( - 0,4091 ):
F(d1) = 0,508465 = 0,5085; F(d2) = 0,341233 = 0,3412.
Подставив полученные значения в формулу Блэка-Шоулза получим оценку стоимости колл-опциона на акции Cisco с ценой исполнения $15:
С = S×F(d1) - X×e-rt× F(d2) = $13,62×0,5085 - $15×exp(-0,0463×0,2822) ×0,3412 =
= $6,92577 – $15 × 0,999018 × 0,3412 = 6,92577 – 5,113471 = $1,81.
Если учесть, что стоимость опциона в цене исполнения составляла:
$15 – $13,62 = $1,38 < $1,81, то колл-опцион был несколько недооценён.
|
|
|


