 |
Основное уравнение молекулярно-кинетической теории.
|
|
|
|
Молекулярно-кинетическая теория основана на законах классической механики и модели идеального газа.
Идеальным называется газ, молекулы которого имеют пренебрежимо малый объем, не взаимодействуют друг с другом на расстоянии и находятся в состоянии хаотического движения.
Замечание 1. При нормальных условиях (давлении pо ~ 105 Па и температуре Т0 ~ 273 К) многие газы можно считать идеальными.
Рассмотрим идеальный одноатомный газ, заключенный в некоторый сосуд объемом V и содержащий N молекул. Стенки сосуда вследствие хаотического теплового движения молекул газа подвергаются бомбардировке молекулами. В результате абсолютно упругих соударений каждому элементу стенки площадью DS за секунду сообщается некоторый импульс, который равен силе, действующей на этот элемент. Отношение этой силы к величине DS и есть давление газа, которое из-за хаотичности движения молекул в состоянии равновесия одинаково на различных участках стенки сосуда и внутри газа. При соударении молекулы со стенкой импульс, передаваемый стенке, будет равен
DK1=2m1v cosq,
где m1 - масса молекулы,
v - ее скорость,
q - угол падения на стенку.
Хаотичность предполагает самые различные направления движения молекул (в сферической системе координат различные углы q и j) и различные модули скоростей молекул. Выделим из всех молекул те dNv молекул, скорости которых заключены в интервале от v до v+dv. Из числа этих молекул выделим те молекулы, направления движения которых заключены в пределах телесного угла dWqj. Их число будет равно: dNvqj = dNvdWqj /4p. Возьмем промежуток времени dt настолько малым, что молекулы не успеют столкнуться между собой до соударения со стенкой. За это время из выделенных молекул до площадки DS долетят только те, которые заключены в косом цилиндре с основанием DS и высотой v cosqdt (рис. 1).
|
|
|
Число таких молекул будет равно:
DNvqj = dNvdWqjDSv cosqdt/(4pV),
где V - объем сосуда (газа).
Тогда полный импульс, передаваемый молекулами элементу поверхности DS за время dt, будет равен:
DKvqj = 2m1v cosq DN vqj = 2m1v2cos2q dNvdWqjDS dt/(4pV).
Проинтегрируем полученное выражение по всем направлениям в пределах телесного угла 2p (q: от 0 до p/2, а j: от 0 до 2p) с учетом того, что dWqj = sin q dq dj:
DKv = 2m1v2DS dt dNv  cos2q sinq dq dj/(4pV) = m1v2DSdt dNv/(3V).
cos2q sinq dq dj/(4pV) = m1v2DSdt dNv/(3V).
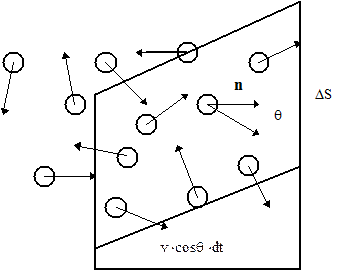
Рис. 1.Соударения молекул со стенкой сосуда
Среднее значение квадрата скорости молекул <v2> определяется выражением:
<v2> = (1/N)  v2dNv.
v2dNv.
Проинтегрировав выражение (5.3) по скоростям от 0 до v max, получим полный импульс, передаваемый молекулами площадке DS за время dt:
DK = m1<v2>DS dt N/(3V) = (1/3)nm1<v2> DS dt,
где n = N/V - число молекул в единице объема.
Разделив полученное выражение на dt, а затем на DS согласно определению давления газа, получим:
p = (1/3)nm1<v2>
Данное уравнение называют основным уравнением молекулярно-кинетической теории идеального газа.
Понятия давления и объема имеют достаточно ясный физический смысл. Более сложным и менее наглядным является понятие температуры. Подойти к этому понятию можно путем следующих рассуждений. Если два разных соприкасающихся тела находятся в состоянии теплового равновесия (не обмениваются энергией), то этим телам приписывается одинаковая температура. Если одно из них (более нагретое) передает энергию другому (менее нагретому), то первому телу приписывается большая температура. Ряд свойств тела (объем, электрическое сопротивление и др.) зависят от температуры и могут быть выбраны для количественной характеристики нагретости. Например, длина столбика жидкости в тонкой стеклянной трубке при нагревании увеличивается (жидкость расширяется). Это свойство можно использовать для измерения температуры, если проградуировать трубку, поступив следующим образом: минимальная длина столбика жидкости при температуре замерзания воды пусть будет соответствовать 0 oC. А длина при температуре кипения воды – 100 оC. Такая шкала будет называться шкалой Цельсия (t). Таким образом, температура выступает как мера нагретости тел. С точки зрения термодинамической системы, находящейся в равновесном состоянии, температура - это мера интенсивности теплового движения молекул или других частиц, образующих систему. В частности, для идеального газа мерой интенсивности теплового движения молекул является средняя кинетическая энергия теплового движения молекулы <e>. Тогда можно количественно определить температуру, исходя из ее пропорциональности средней кинетической энергии молекулы. Для идеального одноатомного газа < e> будет равна:
|
|
|
<e> = m1<v2>/2 = (3/2)kT,
где k = 1,38·10-23 Дж/К - постоянная Больцмана,
Т - абсолютная температура.
Учитывая выражения для < e>, получим основное уравнение молекулярно-кинетической теории в виде:
p = nkT.
Замечание 2. Средняя кинетическая энергия молекул идеального газа учитывает только энергию поступательного движения молекул.
Замечание 3. Т = t + 273,15, где t - температура в градусах Цельсия.
|
|
|


