 |
Число степеней свободы молекулы
|
|
|
|
Физическая величина, однозначно определяемая состоянием термодинамической системы и зависящая от параметров состояния, называется функцией состояния. Функции состояния определяются внутренним строением термодинамической системы и тел, которые эту систему составляют, характером взаимодействия внутри системы. Одну из функций состояния - внутреннюю энергию системы - рассмотрим.
Полная энергия термодинамической системы (W) включает в себя кинетическую энергию механического движения системы как целого Wкмех (или ее макроскопических частей), потенциальную энергию системы во внешнем поле Wпмех и внутреннюю энергию U, зависящую только от внутреннего состояния системы и характера взаимодействий в системе.
W = Wкмех + Wп мех + U.
Внутренняя энергия термодинамической системы (U) включает в себя энергию всевозможных видов движения и взаимодействия частиц (молекул, тел и др.), составляющих данную систему. Например, внутренняя энергия газа состоит:
а) кинетическая энергия поступательного и вращательного движения молекул;
б) энергия колебательного движения атомов в молекуле;
в) потенциальная энергия взаимодействия молекул между собой;
г) энергия электронных оболочек атомов и ионов;
д) энергия ядер атомов.
Все виды движения частиц в термодинамической системе связаны с некоторым запасом энергии, зависящей от числа степеней свободы.
Числом степеней свободы (i) механической системы называется количество независимых величин, с помощью которых задается положение системы. Например, положение материальной точки в пространстве может быть задано с помощью трех координат (x,y,z). В соответствии с этим для материальной точки i = 3. Система из N материальных точек без связей имеет 3N поступательных степеней свободы. Любая жесткая связь уменьшает число степеней свободы на единицу. Так, например, система из двух материальных точек, расстояние между которыми постоянно и равно l, имеет i = 5. Поэтому двухатомная молекула имеет пять степеней свободы. Положение твердого тела можно задать, используя координаты его центра инерции (x,y,z), а также три угла, характеризующие ориентацию тела в пространстве (q, j, y). Таким образом, для твердого тела i = 6. Изменение координат центра инерции тела обусловлено поступательным движением. Поэтому соответствующие степени свободы называются поступательными. Изменение любого из углов связано с вращением тела и соответствует вращательным степеням свободы. Таким образом, твердое тело и трехатомная молекула обладают тремя поступательными и тремя вращательными степенями свободы. Если две материальные точки связаны не жестко (изменяется l), то число степеней свободы i = 6, т. к. добавляются колебательные степени свободы.
|
|
|
Поскольку ни одна из поступательных степеней свободы не имеет преимущества перед остальными, то, как это следует из формулы для средней кинетической энергии молекулы идеального газа, на каждую степень свободы приходится в среднем одинаковая энергия kТ/2. В статистической физике доказывается более общий закон - закон равного распределения энергии по степеням свободы: на каждую степень свободы молекулы приходится в среднем одинаковая энергия, равная kТ/2.
Таким образом, средняя энергия молекулы равна:
<e> = (i/2)kТ.
Замечание. Колебательная степень свободы обладает вдвое большей энергетической емкостью, т.к. при колебаниях система обладает не только кинетической, но и потенциальной энергией. То есть в данном случае
i = nпост + nвращ + 2nколеб,
где nиндекс - число степеней свободы данного вида движения.
Получим выражение для внутренней энергии идеального газа. Из всех составляющих внутренней энергии для этой модели будем учитывать только первую и вторую составляющие внутренней энергии, поскольку молекулы не взаимодействуют на расстоянии, а энергия электронных оболочек и ядерная энергия часто остаются постоянными при протекании различных процессов в термодинамической системе. С учетом средней энергии одной молекулы энергия всех N молекул (внутренняя энергия системы) будет равна: U = N(i/2)kT. Учитывая, что N = NAn, получим выражение для внутренней энергии идеального газа:
|
|
|
U = NAn(i/2)kT= n(i/2)RT.
Таким образом, внутренняя энергия идеального газа пропорциональна абсолютной температуре, является однозначной функцией его состояния и не зависит от того, каким образом достигнуто это состояние.
Внутренняя энергия газа Ван-дер-Ваальса должна включать в себя кроме кинетической энергии и потенциальную энергию взаимодействия молекул друг с другом. Соответствующий расчет приводит к формуле:
U = n(i/2)RT - na/V.
Видно, что внутренняя энергия такого газа также является функцией его состояния, но зависит не только от температуры, но и от объема газа.
Подобно потенциальной энергии в механике внутренняя энергия любой термодинамической системы определена с точностью до постоянного слагаемого, зависящего от выбора состояния, в котором внутренняя энергия равна нулю.
ОСНОВЫ ТЕРМОДИНАМИКИ
Термодинамические процессы. Работа и количество теплоты.
Теплоемкость
Термодинамическим процессом называют всякое изменение состояния термодинамической системы, характеризуемое изменением термодинамических параметров. Термодинамический процесс будет называться равновесным, если в этом процессе система проходит непрерывный ряд бесконечно близких равновесных состояний.
Изопроцессы -этопроцессы, протекающие при одном неизменном термодинамическом параметре состояния системы. При изучении изопроцессов, происходящих в газах при условиях близких к нормальным (идеальный газ), были установлены опытные законы их протекания.
1. Изотермический процесс (Т= const). Для данной массы газа (m) при неизменной температуре, произведение давления газа (р) на его объем (V), есть величина постоянная. Уравнение изотермического процесса может быть получено из уравнения состояния идеального газа.
|
|
|
pV =(m/m)RT = const, m = const.
2. Изохорный процесс (V =const). Давление данной массы газа (m) при постоянном объеме изменяется линейно с изменением температуры:
p = p0(1 + at), m = const,
где p0 - давление газа при 0 0С,
a = 1/273,15 (1/град),
t - температура в градусах Цельсия.
Если ввести абсолютную температуру Т = t + 273,15, то получим:
p = p0aT или p/T = const, m = const.
Данное уравнение можно получить из уравнения состояния идеального газа
pV =(m/m)RT Þ p = (m/m)RT/V Þ p/T = (m/m)R/V = const.
3. Изобарный процесс (р = const). Объем данной массы газа (m) при постоянном давлении изменяется линейно с изменением температуры:
V = V0(1 + at), m = const,
где V0 - объем газа при 0 0С,
a = 1/273,15 (1/град).
Введя абсолютную температуру Т, получим:
V = V0aT или V/T = const, m = const.
Это уравнение можно получить из уравнения состояния идеального газа (5.6).
pV =(m/m)RT Þ V = (m/m)RT/p Þ V/T = (m/m)R/p = const.
Для наглядности термодинамические процессы изображают на различных диаграммах в виде зависимости одного параметра от другого.

а б в
Рис. 2. Графики изопроцессов:
а – изотермические (Т2>Т1); б – изохорные (V1>V2); в - изобарные процессы (р1>р2).
Практически все процессы, протекающие с изменением состояния термодинамической системы, происходят за счет обмена энергией между системой и внешней средой. Обмен энергией может осуществляться двумя качественно различными путями: путем совершения работы внешними телами (или над внешними телами) и путем теплообмена.
При обмене энергией путем совершения работы необходимо перемещать внешние тела, что влечет за собой необходимые изменения внешних параметров самой системы. Поэтому в отсутствии внешних полей совершение работы системой (или над системой) возможно только при изменении объема или формы системы.
При совершении работы энергия упорядоченного движения внешних тел может перейти в энергию хаотического теплового движения молекул или наоборот. Например, газ, расширяющийся в цилиндре двигателя внутреннего сгорания, перемещает поршень и передает ему энергию в форме работы. Для примера получим формулу для работы при изменении объема газа.
|
|
|
Пусть объем газа меняется так мало, что давление практически не изменяется. Выделим на поверхности, ограничивающей газ площадку DSi, которая при изменении объема переместилась на расстояние dh i . Тогда работа газа по перемещению этой площадки будет равна:
dAi = F d r = Fidh i = pDSidhi = pdVi.
Вся работа при бесконечно малом изменении объема газа dV (элементарная работа) будет равна сумме таких работ по всей поверхности:
dA = SdAi = p SdVi = pdV.
Таким образом, работа, совершаемая газом, при бесконечно малом изменении его объема равна произведению давления газа на изменение его объема.
Замечание 1. Работа газа может быть как положительной (газ совершает работу), так и отрицательной (над газом совершают работу).
Замечание 2. Формула для работы справедлива не только для газа, но и для любой термодинамической системы при изменении ее объема.
При изменении состояния системы от состояния 1 к состоянию 2 с изменением ее объема полная работа за весь процесс будет равна сумме элементарных работ:
А12 =  dА =
dА =  pdV.
pdV.
Графически работа изображается площадью под графиком зависимости p от V (рис. 3).
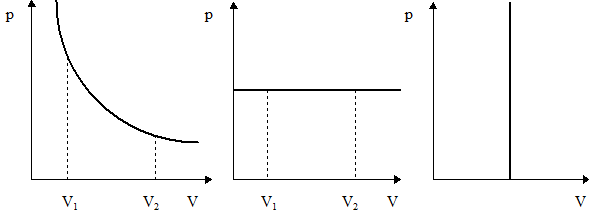
а б в
Рис. 3. Работа для разных термодинамических процессов:
а – изотермический процесс; б – изобарный процесс; в - изохорный процесс
Замечание 3. При изохорном (V = const) процессе А12 = 0, а при изобарном процессе (p = const):
A12 =  pdV = p
pdV = p 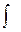 dV = p(V2 - V1) = pDV12.
dV = p(V2 - V1) = pDV12.
Количество энергии, передаваемое от одного тела другому в результате теплообмена, называется количеством теплоты (Q).
Теплообмен происходит между телами, нагретыми до разных температур, и осуществляется тремя способами:
1) конвективный теплообмен - передача энергии в виде теплоты между неравномерно нагретыми частями жидкостей, газов или газами, жидкостями и твердыми телами, при движении жидкостей и газов;
2) теплопроводность - передача энергии от одной части неравномерно нагретого тела к другой за счет хаотического теплового движения молекул;
3) теплообмен излучением - происходит без непосредственного контакта тел, обменивающихся энергией, и заключается в испускании и поглощении телами энергии электромагнитного поля и других излучений.
Сообщение телу небольшого количества теплоты (элементарной теплоты) dQ также может привести к усилению теплового движения его частиц и увеличению внутренней энергии тела. В отличие от внутренней энергии (U) системы понятие теплоты и работы имеют смысл только в связи с процессом изменения состояния системы. Они являются энергетическими характеристиками этого процесса. Поэтому, имеет смысл говорить о бесконечно малом изменении внутренней энергии системы в результате какого-либо процесса (dU) или о передаче какого-либо бесконечно малого количества теплоты dQ, или о совершении элементарной работы dA.
|
|
|
Замечание 4. Математически это означает, что dU - полный дифференциал (бесконечно малое изменение) некоторой функции состояния системы, а dQ и dA - бесконечно малые (элементарные) соответственно теплота и работа, не являющиеся полными дифференциалами.
Для различных процессов интенсивность обмена энергией различна, поэтому для более детальной характеристики процесса вводят понятие теплоемкости, которая в общем случае зависит от способа теплообмена.
Теплоемкость - количество теплоты, необходимое для нагревания тела на 1 К:
C = dQ/dT.
Удельная теплоемкость - количество теплоты, которое необходимо сообщить единице массы вещества для нагревания ее на 1 К:
C уд = dQ/(mdT),
где dQ - подведенное количество теплоты,
m - масса нагреваемого тела,
dТ - изменение температуры, вызванное подведенным теплом dQ.
Молярная теплоемкость - количество тепла, которое необходимо сообщить одному молю вещества для нагревания его на 1 К.
Cмол = dQ/(ndT).
Так как n = m/m, то dQ = CмолmdT/m = C удmdT и Cмол = C удm.
Замечание 5. Количество теплоты, переданное системе, определяется как
dQ = CdT = CудmdT = CмолndT или за весь процесс изменения состояния от состояния 1 к состоянию 2:
Q12 = 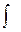 d Q =
d Q = 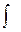 CdT.
CdT.
|
|
|


