Уравнение Клапейрона-Клаузиуса. Изотермы Ван-дер-Ваальса

Фазовыми превращениями называются переходы вещества из одной фазы в другую. Примерами фазовых превращений могут служить изменения агрегатного состояния вещества.

Испарением (парообразованием) называют переход вещества из жидкого состояния в газообразное. Обратный переход называется конденсацией. Переход вещества из твердого состояния, минуя жидкое, в газообразное называется сублимацией (возгонкой). Переход из твердого состояния в жидкое называется плавлением, а обратный переход - кристаллизацией (затвердеванием). Примером сублимации может служить превращение льда в пар при сушке белья зимой. Твердое состояние (и жидкое тоже) вещества может реализоваться в различных кристаллических модификациях, представляющих различные фазы. Такое явление называется полиморфизмом. Например, железо может существовать в 4-х модификациях (a-, b-, g- и d-железо), жидкий гелий в 2-х (жидкий гелий I и II). При изменении температуры T или давления p различные полиморфные модификации могут превращаться друг в друга. Превращение вещества из одной кристаллической модификации в другую называется полиморфным превращением. Например, при температуре T = 595 К g-Fe₂ O₃ (маггемит) превращается в a- Fe₂ O₃ (гематит), отличающийся от первого кристаллической решеткой.

Для большинства переходов вещества из одной фазы в другую характерно выделение или поглощение некоторого количества тепла (скрытой теплоты перехода). Такие переходы называются фазовыми переходами первого рода.

Фазовые переходы второго рода не сопровождаются тепловым эффектом, но изменение некоторых свойств вещества также происходит скачком (теплоемкость, намагниченность и др.). Примерами таких переходов могут быть: переход жидкого гелия I в жидкий гелий II, возникновение сверхпроводящего состояния, переход ферромагнетиков в парамагнитное состояние. Прямые характеристики тела (внутренняя энергия, объем, энтропия и др.), определяющие состояние вещества в точке фазового перехода второго рода, не испытывают скачка, изменяются плавно. Скачок испытывают их производные: теплоемкость C = dE/dT, сжимаемость dV/dp, коэффициент теплового расширения dV/dT и др. При фазовом переходе второго рода изменяется также структура кристаллической решетки и ее симметрия.

Описание процессов испарения, конденсации и других процессов в газах при больших плотностях удобно проводить, используя модель реального газа - Ван-дер-Ваальсовский газ, описанный ранее. Для произвольной массы газа уравнение Ван-дер-Ваальса имеет вид:

(p + n²a/V²)(V - nb) = nRT,

где a,b - поправки Ван-дер-Ваальса, которые можно найти для любого газа опытным путем.

Кривая зависимости между давлением и объемом реального газа при постоянной температуре называется изотермой Ван-дер-Ваальса. Эту кривую можно получить, преобразовав уравнение состояния к виду:

pV³ - (pbn + RTn)V² + n²aV - n³ab = 0.

График такой кривой третьего порядка показан на рис. 25 для некоторой температуры Т.

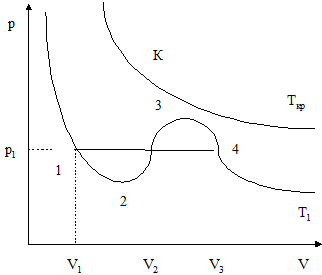
Рис. 25. Изотермы Ван-дер-Ваальса

Видно, что на изотерме Ван-дер-Ваальса одному давлению соответствуют три значения объема V₁,V₂ и V₃. Экспериментальные изотермы отличаются от Ван-дер-Ваальсовских. Если сжимать газ под поршнем при постоянной температуре, то до точки 4 давление увеличивается в соответствии с уравнением изотермы идеального газа. В точке 4 пар становится насыщенным, и давление перестает изменяться при сжатии. При этом пар постепенно переходит в жидкость, и в точке 1 этот процесс завершается. При дальнейшем сжатии давление резко возрастает и соответствует сжиманию жидкости. Часть теоретической изотермы от 4 до точки 3 соответствует метастабильному (неустойчивому) состоянию вещества - пересыщенному пару. Участок 1 - 2 соответствует другому неустойчивому состоянию - перегретой жидкости. Состояния от 2 до 3 на практике осуществить нельзя. С ростом температуры процесса прямолинейные участки укорачиваются и при некоторой температуре T_кр (критической температуре) вырождаются в точку К. Критические параметры p_кр, T_кр и V_кр легко получить из того условия, что точка К является точкой перегиба. При этом dp/dV = 0. Уравнение Ван-дер-Ваальса для одного моля газа можно записать в виде:

V³ - [b + R(T/p)]V² + (a/p)V - a(b/p) = 0.

В критической точке все три корня уравнения совпадают, и уравнение должно иметь вид: (V - V_кр)³ = V³ - 3V²V_{к р} + 3VV_кр² - V_кр³ = 0. Сравнивая коэффициенты в уравнениях, находим, что критические параметры можно выразить по формулам:

V_кр = 3b; p_кр = a/(27b²); T_кр = 8a/(276b).