Тепловые машины. Цикл Карно. Неравенство Клаузиуса

 

Закон сохранения энергии не позволяет определить направление протекания процессов. Для этого необходимо расширить представления о термодинамических процессах. Термодинамический процесс называется обратимым, если после него можно возвратить систему и все взаимодействовавшие с ней тела в исходное состояние через те же промежуточные состояния. В противном случае термодинамический процесс будет необратимым.

Замечание 1. Всякий обратимый процесс будет равновесным.

Примером обратимого процесса могут служить незатухающие колебания осциллятора, при которых один вид энергии превращается в другой. Примером необратимых процессов могут служить те, которые сопровождаются трением. За счет силы трения механическая энергия системы превращается в тепловую (внутреннюю энергию системы и внешней среды). В данном случае прямой процесс превращения механической энергии в тепловую протекает самопроизвольно. Для осуществления обратного процесса необходимо, чтобы энергия, выделившаяся при охлаждении системы и внешней среды, вновь превратилась в механическую энергию системы. Опыт показывает, что хаотическое движение атомов и молекул тел системы и внешней среды не может самопроизвольно привести к увеличению механической (кинетической) энергии системы. Для осуществления такого процесса необходим компенсирующий процесс передачи системой и внешней средой третьему телу теплоты и совершения над этим телом работы. Поэтому, хотя система и вернется в исходное состояние, состояние внешних тел изменится. Другим примером необратимых процессов могут служить процессы теплообмена. В таких процессах энергия атомов и молекул более нагретого тела уменьшается, а менее нагретого - увеличивается. В итоге - температура тел самопроизвольно выравнивается. Обратный процесс передачи тепла от тела, имеющего такую же температуру, другому телу самопроизвольно протекать не может. Для осуществления такого процесса необходимо холодильное устройство (третье тело), работа которого неизбежно изменит состояние других внешних тел. Все реальные процессы протекают при наличии сил трения и теплообмена и, следовательно, являются необратимыми. Однако в некоторых случаях приближенно их можно считать обратимыми.

Круговым процессом или циклом называется такая совокупность термодинамических процессов, в результате которых система возвращается в исходное состояние. Равновесные круговые процессы на всех диаграммах изображаются замкнутыми кривыми, т.к. началу и концу кругового процесса соответствует одна и та же точка - те же термодинамические параметры и одинаковое состояние системы. Тело (система тел), совершающее цикл и обменивающееся энергией с другими телами, называется рабочим телом. Обычно рабочим телом является газ. Круговые процессы лежат в основе всех тепловых машин (двигателей, тепловых турбин, холодильных машин и т.п.).

Рассмотрим произвольный круговой процесс на графике в координатах p и V (рис. 5).

Рис. 5. Круговой термодинамический процесс

Разобьем его на два процесса: расширение из состояния 1 в состояние 2 (кривая 1С₁2) и сжатие из состояния 2 в состояние 1 (кривая 2С₂1). Работа газа за весь цикл А₀ равна сумме работ, совершавшихся на всех участках: А₀ = А₁₂ + А₂₁, где работа расширения газа А₁₂ = pdV - площадь фигуры V₁1С₁2V₂ > 0, работа сжатия A₂₁ = pdV - площадь фигуры V₁1C ₂2V₂<0. Так как A₁₂ > 0, A₂₁ < 0 и |A₁₂|>|A₂₁|, то A₀ = площадь цикла > 0.

Рассмотренный процесс называется прямым циклом, при котором расширение происходит при более высоких давлении и температуре, чем сжатие, и работа цикла положительна (рабочее тело совершает работу над внешними телами).

При этом, согласно первому началу термодинамики, в результате расширения рабочее тело получило количество теплоты

Q₁₂ = A₁₂ + (U₂ - U₁),

где U₁ и U₂ внутренняя энергия рабочего тела в состоянии 1 и 2 соответственно.

В результате сжатия - Q₂₁ = A₂₁ + (U₁ - U₂). Обозначим абсолютную величину количества теплоты, переданного от более нагретого тела рабочему телу Q₁, а отданного рабочим телом менее нагретому телу - Q₂. Тогда, Q₁₂ = Q₁ , а Q ₂₁ = - Q₂. Q ₁ - Q₂ = Q₁₂ + Q₂₁ = A₁₂ + A₂₁ = A > 0.

Устройство, совершающее прямой цикл, называется тепловой машиной. Для осуществления прямого цикла (тепловой машины) кроме рабочего тела необходимы: а) нагреватель - более нагретое (Т₁) тело, передающее тепло рабочему телу; б) холодильник - менее нагретое (Т₂) тело, принимающее тепло от рабочего тела (рис.6).

 

 

Рис. 6. Принципиальная схема тепловой машины

Замечание 2. В тепловой машине только часть тепла, полученного от нагревателя, превращается в работу:

Q₁ - Q₂ = A.

Коэффициент полезного действия (КПД,h) тепловой машины есть отношение работы, совершенной рабочим телом, к количеству теплоты, переданного ему нагревателем:

h = A/Q₁ = (Q₁ - Q₂)/Q₁ < 1.

Если бы круговой процесс, рассмотренный нами, протекал в обратном направлении, то суммарная работа A стала бы отрицательной. Такой цикл называется обратным. Примером обратного цикла может служить круговой процесс, совершаемый рабочим телом в холодильной машине, которая за счет работы, совершаемой внешними телами над рабочим телом, осуществляет перенос тепла от менее нагретых тел более нагретым.

Рассмотрим обратимый круговой процесс, состоящий из четырех обратимых процессов: двух изотермических и двух адиабатных. Такой круговой процесс был впервые изучен С. Карно (1824) и называется циклом Карно.

Идеальная тепловая машина - машина без потерь, работающая по циклу Карно. Проведем анализ машин, работающих по циклу Карно, где рабочим телом является идеальный газ. Рассмотрим сначала прямой цикл Карно (рис.7), состоящий из:

12 - изотермический процесс расширения газа при температуре нагревателя Т₁;

23 - адиабатный процесс расширения газа;

34 - изотермический процесс сжатия газа при температуре холодильника Т₂;

41 - адиабатный процесс сжатия.

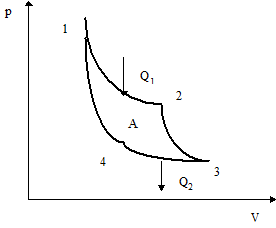
Рис.7. Цикл Карно и идеальная тепловая машина

В таком цикле теплообмен происходит только при изотермических процессах: как показывают полученные ранее формулы, количество теплоты, переданное газу в процессе 12, равно:

Q₁₂ = nRT₁ln(V₂/V₁) = Q₁,

а в процессе 34:

Q₃₄ = nRT₂ln(V₄ /V₃) = - Q₂ .

По определению: h = [nRT₁ln(V₂/V₁)] + [nRT₂ln(V₄ /V₃)]/[ nRT₁ln(V₂/V₁)]. Упростим это выражение, используя уравнение Пуассона для процессов 23 и 41:

p₂V₂^g/(p₁V₁^g) = p₃V₃^g/(p₄V₄^g).

Согласно уравнению изотермического процесса:

p₁V₁ = p₂V₂ и p₃V₃ = p₄V₄.

Решая совместно уравнения, получаем, что ln(V₂/V₁) = - ln(V₄/V₃). Тогда выражение для КПД цикла Карно примет вид:

h_К = (T₁ - T₂)/T₁.

В обратном цикле Карно (холодильная машина) количество теплоты Q₁’ отводится от рабочего тела в изотермическом процессе при температуре Т₁ (процесс 21), а количество теплоты Q₂ - подводится к рабочему телу в изотермическом процессе при температуре Т₂ (процесс 43). При этом за счет работы внешнего тела A’ над рабочим телом осуществляется передача тепла от менее нагретого тела к более нагретому. Величина, равная отношению теплоты, отданной в обратном цикле от охлаждаемого тела, к работе, затраченной в этом цикле, называется холодильным коэффициентом.

k = Q_отв/A’= Q₂ /A’= Q₂ /(Q₁ ’- Q₂) = T₂ /(T₁ - T₂).

Из определения к.п.д. и выражения для к.п.д. цикла Карно следует:

(Q₁ - Q₂)/Q₁ = (T₁ - T₂)/T₁ или Q₁ /T₁ + Q₂ ’/T₂ = 0,

где теплота, отданная рабочим телом холодильнику, обозначена Q₂ ’ = - Q₂.

Отношение количества теплоты, переданного системе (рабочему телу), к температуре, при которой происходит передача тепла, называется приведенной теплотой. Видно, что для цикла Карно (обратимого цикла) сумма приведенных теплот равна нулю. Справедливо и более общее утверждение, называемое теоремой Клаузиуса: для любого кругового обратимого процесса сумма приведенных теплот равна нулю и не зависит от конкретного вида этого процесса.

SQ_i/T_i = 0 или dQ/T = 0.

Аналогичное соотношение можно доказать и для произвольного кругового обратимого процесса. Такой процесс можно представить в виде совокупности бесконечно малых процессов - циклов Карно, для каждого из которых сумма приведенных теплот будет равна нулю. Суммируя приведенные теплоты по каждому циклу (нули) получим в итоге нуль.

Замечание 3. Количество теплоты (Q_i или dQ) берется со знаком “плюс”, если система получает тепло, и со знаком “минус”, если отдает.

Для необратимого кругового процесса легко показать, что его к.п.д. меньше к.п.д. цикла Карно при идентичных значениях температур нагревателя и холодильника. Действительно, рабочее тело в данном случае отдает часть теплоты внешним телам. Поэтому Q₂>Q_2K , тогда h_необр = (Q₁ - Q₂ )/Q₁ < h_К = (T₁ - T₂ )/T₁. Повторив проведенные выше рассуждения для необратимых циклов, получим, что

Q₁/T₁ + Q₂’/T₂ < 0.

Таким образом, справедливо более общее утверждение (неравенство Клаузиуса): для любого кругового процесса выполняется неравенство:

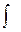dQ/T³ 0.

Замечание 4. Знак неравенства соответствует необратимому процессу, знак равенства - обратимому.

Энтропия. Теорема Карно

 

Кроме термодинамических параметров p, V, T и функции состояния системы - внутренней энергии U, в термодинамике используются и другие функции состояния системы. Особое место среди них занимает энтропия. Как это следует из теоремы Клаузиуса, для любого бесконечно малого обратимого процесса отношение dQ/T есть полный дифференциал некоторой функции состояния системы, которая называется энтропией.

dS = dQ/T.

Для любого конечного процесса интеграл вида:

S₂ - S₁ = 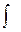dQ/T,

выражает изменение энтропии.

Каждому состоянию системы соответствует определенное значение энтропии S (подобно внутренней энергии U). Энтропия системы как целого равна сумме энтропий отдельных частей системы, т.е. энтропия аддитивная величина. Как видно из определения энтропии, можно рассчитать только ее изменение, а не саму энтропию. Однако для термодинамики, изучающей в основном различные процессы в веществе, этого вполне достаточно. В расчетные формулы при описании различных процессов будет входить изменение энтропии. То же самое можно сказать и о внутренней энергии. dS и dQ имеют одинаковые знаки. Это позволяет судить о направлении теплообмена по изменению энтропии. Например, при нагревании тела (dQ > 0) его энтропия возрастает. При адиабатном процессе (dQ = 0) энтропия системы не изменяется. Весьма полезно многие процессы изображать на диаграмме в координатах T - S (T - S диаграммы). Рассмотрим любой обратимый процесс в координатах T - S (рис. 8).

Рис. 8. Теорема Карно и максимальный КПД тепловой машины

Из определения энтропии следует, что для обратимого процесса dQ = TdS. Количество теплоты, сообщенное системе в процессе 12, будет равно площади всей фигуры S₁12S₂:

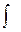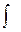Q₁₂ = dQ = TdS.

Используя T - S диаграмму можно доказать теорему Карно: к.п.д. цикла Карно максимален и не зависит от природы рабочего тела и конструкции идеальной тепловой машины, а определяется только температурами нагревателя и холодильника.

Рассмотрим любой произвольный обратимый круговой процесс аbсdа. Как видно из диаграммы, к рабочему телу в процессе abc подводится тепло Q₁ = 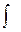TdS > 0. В процессе cda отводится Q₂’= - Q₂ = 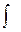TdS < 0. Работа за весь цикл A соответствует площади, ограниченной замкнутой кривой abcda. По определению h_обр = A/Q₁. В частности для цикла Карно (рис. 8):

h_K = (T₁ -T₂ )(S₂ -S₁)/[T₁ (S₂ - S₁)] = (T₁ - T₂ )/T₁,

без каких либо ограничений на тип рабочего тела и идеальной тепловой машины. Полученная формула совпадает с формулой, полученной ранее в предположении, что рабочим телом является идеальный газ.

Из диаграммы для произвольного обратимого цикла видно, что

Q₁ = T₁(S₂ - S₁) - (A₁ +A₂), а Q₂ = T₂(S₂ - S₁) + (A₃ + A₄). Тогда h_обр = (Q₁ - Q₂)/Q₁ =

= [T₁(S₂ - S₁) - (A₁ +A₂) - T₂(S₂ - S₁) - (A₃ + A₄)]/ [T₁(S₂ - S₁) - (A₁ +A₂)] =

= [T₁(S₂ - S₁) - T₂(S₂ - S₁) - (A₁ +A₂ + A₃ +A₄)]/[T₁(S₂ - S₁) - (A₁ +A₂)], или

h_обр = ,

где - k = (A₁+A₂ + A₃ +A₄)/[(T₁ - Т₂)(S₂ - S₁), k’= (A₁+A₂))/[(T₁ - Т₂)(S₂ - S₁).

Очевидно, что k >k’. Тогда (1-k)/(1-k’) < 1, что доказывает максимальность КПД цикла Карно по сравнению с другими циклами (h_обр £ h_К).

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: