 |
Пакеты прикладных программ. Базы знаний и экспертные системы. Системы поддержки решений. Построение математической модели задачи
|
|
|
|
Пакеты прикладных программ.
Широко используется пакет программ для статистической обработки данных STATISTICA. Этот пакет предназначен для решения задач выбора в условиях стохастической неопределённости. Пакет прикладных программ MS Project относится к классу методо-ориентированного прикладного программного обеспечения. Методология работы данной системы управления основаны на принципах календарного планирования и управления, то есть на моделировании деятельности, направленной на достижение конечной цели, для любой предметной области.
Базы знаний и экспертные системы
Следующее направление – создание баз знаний и экспертных систем. В настоящее время это, пожалуй, главный путь движения к " искусственному интеллекту".
Экспертные системы имеют широкие перспективы: известны их многочисленные практические реализации в разнообразных предметных областях. Некоторые важные принципы организации экспертных систем могут даже учитывать расплывчатость терминов естественного языка.
Системы поддержки решений
Это третье направление представлено системами " интерактивной оценки решений" и особенно " системами поддержки решений" (DSS – Decision Support Systems).
Системы поддержки решений ориентированы не на автоматизацию функций лица, принимающего решения, а на предоставление ему помощи в поиске хорошего решения. Конечно, в математическое и программное обеспечение систем поддержки решений входят и формализованные процедуры, которые лицо, принимающее решения, может использовать в любой нужный ему степени. В качестве доступного примера можно привести систему поддержки принятия решений " Выбор" - аналитическую систему, основанную на методе анализа иерархий (МАИ). Является простым и удобным средством, которое обеспечивает следующие функции: структурирование проблемы; построение набора альтернатив; выделение характеризующих их факторов. Данная СППР осуществит задание значимости этих факторов; оценка альтернативы по каждому из факторов; нахождение неточности и противоречия в суждениях лица, принимающего решение (ЛПР или эксперта); ранжирование альтернатив; помощь в проведении анализа решения и обоснования полученных результатов.
|
|
|
Построение математической модели задачи
Построение математической модели задачи принятия решения (ЗПР) состоит в задании трех множеств: [1]
X – множества допустимых альтернатив;
Y – множества возможных состояний среды;
A – множества возможных исходов.
Множество Х должно содержать не меньше 2 альтернатив, иначе проблемы выбора не существует. Альтернативы рассматриваются как управляющие воздействия, а исходы как состояние управляемой подсистемы. Тогда каждой паре (х, у), определяющей состояние управляемой подсистемы, соответствующей выбранному воздействию х из множества X (  ) и состоянию среды y из множества Y
) и состоянию среды y из множества Y 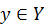 , соответствует определенный исход a из множества A (
, соответствует определенный исход a из множества A (  ). Говоря математическим языком, определена функция F, которая называется функцией реализации. Функция реализации каждой паре (альтернатива, состояние среды) ставит в соответствие определяемый этой функцией исход.
). Говоря математическим языком, определена функция F, которая называется функцией реализации. Функция реализации каждой паре (альтернатива, состояние среды) ставит в соответствие определяемый этой функцией исход.
Набор объектов < X, Y, F, A> представляет реализационную структуру принятия решения. Эта структура выражает связь между выбранной альтернативой и исходом, которая в общем случае не является однозначной, или детерминированной. Каждый конкретный исход зависит не только от выбранной альтернативы, но и от состояния среды.
В зависимости от вида информации в подсистеме о состоянии среды выделяют различные типы задач принятия решений.
|
|
|
§ Принятие решений в условиях определенности определяется тем, что состояние среды является неизменным, фиксированным, причем в самой управляющей системе известно, каково это состояние.
§ Принятие решений в условиях неопределенности происходит, когда кроме знания самого множества возможных состояний среды, никакой дополнительной информации о конкретном состоянии среды системе не известно.
§ Принятие решений в условиях риска означает, что в управляющей системе имеется информация о состоянии среды стохастического, то есть случайного характера. Например, может быть задано распределение вероятностей на множестве состояний среды.
§ Принятие решений в теоретико-игровых условиях имеет место в случаях, когда среда трактуется как одна или несколько целенаправленных подсистем.
Следующей компонентой задачи принятия решений является ее оценочная структура. В то время как реализационная структура определяет возникающий результат, оценочная структура дает оценку полученного результата с точки зрения лица, принимающего решение. В математической модели оценочная структура задаваться как «полезность», «ценность» принятого решения с точки зрения его эффективности. При этом для каждого исхода  можно оценить его полезность некоторым числом
можно оценить его полезность некоторым числом  , тогда оценочная структура задается в виде пары
, тогда оценочная структура задается в виде пары  , где
, где 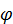 является отображением множества А на множество R, при этом
является отображением множества А на множество R, при этом 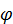 называется оценочной функцией.
называется оценочной функцией.
По-другому способу задания оценочной структуры указываются отношения предпочтения исходов, когда перечисляются пары исходов (а1, а2), для которых а1 лучше, чем а2. Это записывается в виде отношения 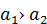 , что означает: а1 предпочтительнее а2
, что означает: а1 предпочтительнее а2
Целевая функция f есть композиция функции реализации F и оценочной функции 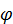 , то есть
, то есть  .
.
Смысл целевой функции заключается в выражении: число 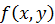 есть оценка полезности того исхода, который возникает в ситуации, когда лицо, принимающее решение, выбирает альтернативу х, а среда принимает состояние у. Если в задаче принятия решения оценка исхода характеризует его в противоположном смысле, являясь выражением затрат, то целевая функция называется функцией потерь.
есть оценка полезности того исхода, который возникает в ситуации, когда лицо, принимающее решение, выбирает альтернативу х, а среда принимает состояние у. Если в задаче принятия решения оценка исхода характеризует его в противоположном смысле, являясь выражением затрат, то целевая функция называется функцией потерь.
В зависимости от того, является ли мощность множества критериев одноэлементным или состоит из нескольких критериев, выделяют следующие типы.
|
|
|
§ задачи принятия решений со скалярным критерием (однокритериальная задача);
§ задачи принятия решений с векторным критерием (многокритериальные задачи).
В зависимости от типа системы - отображает предпочтения одного лица или коллектива, поэтому
§ задачи индивидуального принятия решений;
§ задачи группового принятия решений.
В задаче принятия решений в условиях определенности состояние среды является неизменным и в управляющей системе известно, каково это состояние. При такой постановке задачи исход однозначно выбором альтернативы, и тогда выбор альтернативы эквивалентен исходу. Из этого вытекают следующие утверждения.
1. Альтернативы и исходы отождествляются, следовательно, Х=А.
2. Целевая функция f становится функцией только переменной х.
Тогда в условиях определенности построение математической модели задачи принятия решения можно представить поэтапно следующим образом.
На первом этапе задается множество допустимых альтернатив Х и формулируется целевая функция f на множестве Х.
На втором этапе вводится понятие оптимального решения и находится это решение. Поскольку функция f(x) является оценкой полезности альтернативы х , то на множестве допустимых альтернатив возникает отношение нестрогого предпочтения. Альтернатива х1 считается не менее предпочтительной, чем альтернатива х2, если полезность альтернативы х1 не меньше полезности альтернативы х2:
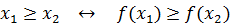
В таком случае принимается единственная концепция оптимальности – оптимальной считается та альтернатива 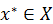 , которая считается не менее предпочтительной, чем любая другая допустимая альтернатива
, которая считается не менее предпочтительной, чем любая другая допустимая альтернатива  . Другими словами, оптимальная альтернатива должна доставлять максимальное значение целевой функции.
. Другими словами, оптимальная альтернатива должна доставлять максимальное значение целевой функции.
В случае, когда целевая функция некоторой задачи задается как функция потерь, при задании отношения предпочтения на множестве Х знак будет заменен на противоположный. Оптимальной будет являться та альтернатива, которая будет доставлять минимальное значение целевой функции потерь.
|
|
|
В целом, построение математической модели задачи принятия решений в условиях определенности необходимо осуществить в три этапа:
1. Определение X – множества допустимых альтернатив.
2. Задание целевой функции f на множестве Х.
3. Нахождение максимума или минимума целевой функции f на множестве Х.
Далее предстоит решить вопрос: существует ли это оптимальное решение, и если оно существует, то как его найти?
Если множество альтернатив конечно, то решение всегда существует, так как на конечном множестве всегда есть наибольшее и наименьшее значение.
Если множество допустимых альтернатив бесконечно, то решение задачи зависит от структуры допустимых альтернатив и от вида целевой функции. Поскольку множество допустимых альтернатив в математической модели принятия решений как правило, определяется числовыми значениями и представляет собой некоторую область допустимых решений 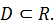 В таком случае целевая функция f есть числовая функция, заданная на числовом множестве D, и нахождение максимального или минимального значения этой функции сводится к математической задаче на экстремум функции в некоторой допустимой области.
В таком случае целевая функция f есть числовая функция, заданная на числовом множестве D, и нахождение максимального или минимального значения этой функции сводится к математической задаче на экстремум функции в некоторой допустимой области.
Рассмотрим эту задачу в общем виде.
Пусть функция y=f(x), график которой изображен на рисунке, непрерывна в некоторой области определения. Значение функции в точке x1 будет больше значений функции во всех соседних точках как слева, так и справа от x1. В этом случае говорят, что функция имеет в точке x1 максимум. В точке x3 функция, очевидно, также имеет максимум. В точке x2, наоборот, значение функции меньше всех соседних значений. В этом случае говорят, что функция имеет в точке x2 минимум. В точки x4 функция f(x) также имеет
 |
минимум.
Функция y=f(x) в точке x0 имеет максимум, если значение функции в этой точке больше, чем ее значения во всех точках некоторого интервала, содержащего точку x0, т. е. если существует такая окрестность точки x0, что для всех x≠ x0, принадлежащих этой окрестности, имеет место неравенство f(x) < f(x0).
Функция y=f(x) имеет минимум в точке x0, если существует такая окрестность точки x0, что для всех x≠ x0, принадлежащих этой окрестности, имеет место неравенство f(x) > f(x0).
Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции .
Обратим внимание на то, что функция, определенная на отрезке, может достигать максимума и минимума только в точках, заключенных внутри рассматриваемого отрезка.
|
|
|
Отмети, что если функция имеет в точке максимум, то это не означает, что в этой точке функция имеет наибольшее значение во всей области определения. На рисунке, рассмотренном выше, функция в точке x1 имеет максимум, хотя есть точки, в которых значения функции больше, чем в точке x1. В частности , f x1) < f(x4), то есть, минимум функции больше максимума. Из определения максимума следует только, что это самое большое значение функции в точках, достаточно близких к точке максимума.
Теорема. (Необходимое условие существования экстремума. ) Если дифференцируемая функция y=f(x) имеет в точке x= x0 экстремум, то ее производная в этой точке обращается в нуль.
Данная теорема утверждает, что точки максимума и минимума могут находиться только среди тех значений аргумента, при которых производная обращается в нуль.
Мы рассмотрели случай, когда функция во всех точках некоторого отрезка имеет производную. Как же обстоит дело в тех случаях, когда производная не существует? Рассмотрим примеры.
Примеры.
1. y=|x|.
Функция не имеет производной в точке x=0 (в этой точке график функции не имеет определенной касательной), но в этой точке функция имеет минимум, так как y(0)=0, а при всех x≠ 0
y > 0.
2. Функция  не имеет производной при x=0, так как не имеет производной при x=0, так как 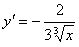 обращается в бесконечность при x=0. Но в этой точке функция имеет максимум.
3. Функция обращается в бесконечность при x=0. Но в этой точке функция имеет максимум.
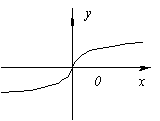
3. Функция 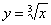 не имеет производной при x=0, так как не имеет производной при x=0, так как  при x→ 0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x)=0 и при x< 0 f(x)< 0, а при x> 0 f(x)> 0. при x→ 0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x)=0 и при x< 0 f(x)< 0, а при x> 0 f(x)> 0.
|    
|
Таким образом, из приведенных примеров и сформулированной теоремы видно, что функция может иметь экстремум лишь в двух случаях:
1) в точках, где производная существует и равна нулю;
2) в точке, где производная не существует.
Однако если в некоторой точке x0 мы знаем, что f '(x0)=0, то отсюда нельзя делать вывод, что в точке x0 функция имеет экстремум.
Например, рассмотрим
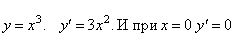 .
.
Но точка x=0 не является точкой экстремума, поскольку слева от этой точки значения функции расположены ниже оси Ox, а справа выше.
Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются критическими точками. Из всего вышесказанного следует, что точки экстремума функции находятся среди критических точек, и, однако, не всякая критическая точка является точкой экстремума. Поэтому, чтобы найти экстремум функции, нужно найти все критические точки функции, а затем каждую из этих точек исследовать отдельно на максимум и минимум. Для этого служит следующая теорема.
Теорема. (Достаточное условие существования экстремума. ) Пусть функция непрерывна на некотором интервале, содержащем критическую точку x0, и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки x0 ). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то в точке x =x0 функция имеет максимум. Если же при переходе через x0 слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум.
Таким образом, если
f '(x) > 0 при x< x0 и f '(x)< 0 при x> x0, то x0 – точка максимума;
 при x< x0 и f '(x)> 0 при x> x0, то x0 – точка минимума.
при x< x0 и f '(x)> 0 при x> x0, то x0 – точка минимума.
 Проиллюстрируем смысл этой теоремы на рисунке. Пусть f '(x1)=0 и для любых x, достаточно близких к x1, выполняются неравенства
Проиллюстрируем смысл этой теоремы на рисунке. Пусть f '(x1)=0 и для любых x, достаточно близких к x1, выполняются неравенства
f '(x)< 0 при x< x1, f '(x)> 0 при x> x1.
Тогда слева от точки x1 функция возрастает, а справа убывает, следовательно, при x =x1 функция переходит от возрастания к убыванию, то есть имеет максимум.
Аналогично можно рассматривать точки x2 и x3.

Схематически все вышесказанное можно изобразить на картинке:
|
|
|


