2.2.Метод линейного программирования.

Задачи линейного программирования (ЛП или ЗЛП) являются частным случаем оптимизационных задач, в которых целевая функция является линейной и функциональные ограничения представляют собой систему линейных неравенств относительно вектора переменных Х, принимающего любые значения из некоторого множества допустимых значений D. Стандартная задача линейного программирования записывается в виде:

;

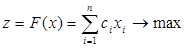x_i ³ 0, i=1, …, n

К задачам линейного программирования также относятся случаи, когда требуется вместо максимума найти минимум целевой функции, в системе ограничений знаки неравенств могут принимать противоположные значения, или иметь строгое равенство.

Число неизвестных n (число компонент вектора Х) и число уравнений m в системе могут быть разными. Как известно из курса линейной алгебры, в этом случае для системы уравнений возможны варианты: система может быть несовместной, то есть не иметь решений вообще; решение может быть одно, но это единственное решение может оказаться недопустимым из-за наличия отрицательных компонент в решении; решений может быть бесконечно много. Вообще же для единственности решения задачи ЛП не требуется равенства числа переменных и числа ограничений. Для задач ЛП разработаны многочисленные эффективные методы решения и соответствующее математическое обеспечение для различных ситуаций.

В рамках задачи линейного программирования решаются задачи принятия решений, касающиеся планирования объемов производства, задача о составлении смеси, распределительные задачи, к которым, в частности относятся транспортная задача и задача о назначениях.

В случае наличия только двух переменных (двух компонент вектора Х) задачу можно решить графическим методом, распространенным классическим методом решения является симплексный метод решения ЗЛП. Эти методы рассматриваются в теории исследования операций (ИО) в рамках использования математических методов в прикладных целях.

В качестве средства поддержки принятия решений в данном случае можно использовать пакет прикладных программ Microsoft Office, которое в электронных таблицах Excel имеет встроенное средство «Поиск решения» (Solver), позволяющее решать задачи линейного и нелинейного программирования.

Эта надстройка в версиях Excel выше 2007 находится на вкладке Данные в группе Анализ. ЕслиВы ее там не обнаружите, значит, она в вашей реализации еще не устанавливалась и чтобы ее использовать, необходимо сначала загрузить ее. Для этого надо выполнить следующие действия.

1. Откройте вкладку Файл и выберите пункт Параметры.

2. Выберите команду Надстройки, а затем в поле Управление выберите пункт Надстройки Excel.

3. Нажмите кнопку Перейти.

4. В окне Доступные надстройки установите флажок Поиск решения и нажмите кнопку ОК.

1. Совет. Если надстройка Поиск решения отсутствует в списке поля Доступные надстройки нажмите кнопку Обзор, чтобы найти ее.

2. Если появится сообщение о том, что надстройка " Поиск решения" не установлена на компьютере, нажмите кнопку Да, чтобы установить ее.

5. После загрузки надстройки " Поиск решения" в группе Анализ на вкладки Данные становится доступна команда Поиск решения.

Надстройка " Поиск решения" является частью набора команд, которые иногда называют средствами анализа " что-если". С помощью этой надстройки можно найти оптимальное значение (максимум или минимум) функции, формула которой содержится в одной ячейке, называемой целевой, с учетом ограничений на значения в других ячейках с формулами на листе. Надстройка " Поиск решения" работает с группой ячеек, называемых ячейками переменных решения или просто ячейками переменных, которые обязательно должны быть включены в расчет формул в целевых ячейках и ячейках ограничения. Надстройка " Поиск решения" изменяет значения в ячейках переменных решения согласно пределам ячеек ограничения и выводит результат в целевой ячейке. В более ранних версиях надстройки " Поиск решения" ячейки переменных решения назывались изменяемыми ячейками.