 |
Условие n > m - непременное требование для задач оптимизации.
|
|
|
|
Условие n > m - непременное требование для задач оптимизации.
Надо из бесчисленного множества решений выбрать одно, которое является оптимальным. Оптимальность решения определяется по критерию. Критерий называется целевой функцией.
Рассмотрим задачу на планирование производства.
Фирма производит три вида продукции ( А, В, С), для выпуска каждого требуется определенное время обработки на всех 4 устройствах I, II, III, IY
| Вид продукции | Время обработки, ч | Прибыль, долл. | |||
| I | II | III | IV | ||
| А | |||||
| В | |||||
| С | |||||
Известно, что время работы на устройствах соответственно 84, 42, 21 и 42 часа. Определите, какую продукцию и в каких количествах стоит производить для максимизации прибыли. (Рынок сбыта для каждого продукта неограничен).
Для составления математической модели необходимо ответить на три вопроса:
1. Что является переменными задачи?
2. Какова цель задачи?
3. Какие условия являются ограничениями?
Отвечаем на эти вопросы.
1. В данной задаче необходимо найти объемы производимой продукции, следовательно, неизвестными являются количества продукции вида А, вида В, вида С – соответственно обозначаемые х1, х2, х3.
2. Целью является максимизация прибыли от реализации продукции, следовательно, зная прибыль (3, 6, 4 доллара от реализации продукции х1, х2, х3 соответственно) и объемы продукции, можно составить целевую функцию F=f(х1, х2, х3) =3х1+6х2+ 4х3
3. Условиями ограничений является то, что для выпуска каждого вида продукции требуется определенное время обработки на всех 4 устройствах I, II, III, IY и время работы на устройствах ограничено соответственно 84, 42, 21 и 42 часа. Отсюда можно записать систему функциональных ограничений –
|
|
|
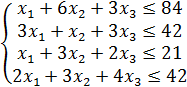
И ограничения на переменные – граничные условия запишутся так
х1, х2, х3≥ 0, х1, х2, х3 - целое.
Для решения можно воспользоваться средством Поиск решения в Excel.
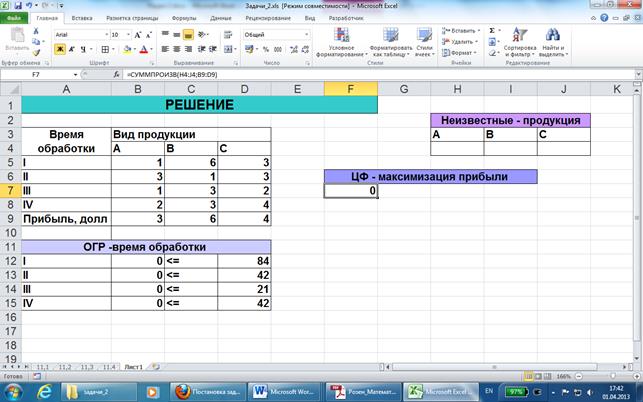
Подготовим лист с данными следующим образом.
Неизвестные будут находится в ячейках H4: J4.
В целевой ячейке F7 записана функция =СУММПРОИЗВ(H4: J4; B9: D9).
В ячейках с ограничениями В12: В15 записаны следующие формулы:
=СУММПРОИЗВ($H$4: $J$4; B5: D5)
=СУММПРОИЗВ($H$4: $J$4; B6: D6)
=СУММПРОИЗВ($H$4: $J$4; B7: D7)
=СУММПРОИЗВ($H$4: $J$4; B8: D8)
Обратите внимание, что ссылка на неизвестные, записанные в ячейках H4: J4 являются абсолютными $H$4: $J$4. Знак $ означает абсолютную ссылку, тогда формулу ограничения можно ввести только в ячейку В12 и скопировать протягиванием до В15. Для проставления абсолютной ссылки используйте клавишу F4.
Вызовем окно Поиск решения и заполним:
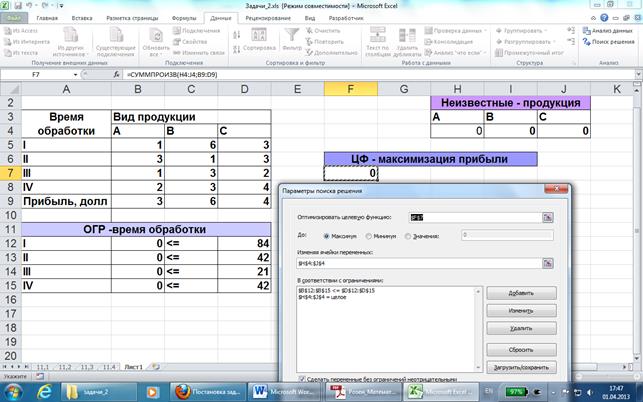
При добавлении условия целостности надо выбрать знак отношения цел:
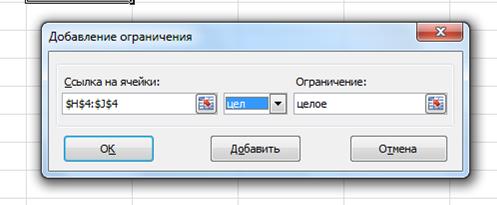
После выполнения получаем:

Таким образом, мы получили, что получения максимальной пробыли, составляющей 54 доллара, продукцию А необходимо выпускать в количестве 12 единиц, продукцию В – 3 единицы, а продукцию С выпускать невыгодно.
Задача о составлении смеси.
Задачи составления смеси широко распространены. Сюда относятся задачи составления диеты, когда необходимо составить рацион питания с соблюдением необходимого уровня ценных питательных веществ или рацион кормления животных, требующий при соблюдении уровня содержания необходимых веществ, минимума затрат на приобретение корма. Если для составления диеты применение такого рода решения проблематично из-за наличия множества предпочтений, то для состава кормления животных метод широко используется и даже выпускаются справочные пособия по рациону кормления, рассчитанные с помощью решения ЗЛП.
Кроме того, существует класс задач, связанный с составлением различных смесей, например, состава удобрения, состава для окрашивания, а также получение сплавов металлов или других составляющих.
|
|
|
Такие задачи составляются преимущественно на минимизацию целевой функции – минимизацию расходов на приобретение состава смеси. При этом ограничения формируются исходя из того, что необходимо иметь не менее определенного количества ингредиентов смеси, а также иногда и не более какого количества некоторых ингредиентов.
Построим математическую модель задачи на составление смеси. Рассмотрим задачу.
Фирма выпускает 2 набора удобрений для газонов: обычный и улучшенный. В обычный набор входят: 3кг азотных, 4кг фосфорных, 1кг калийных удобрений, а в улучшенный входят: 2кг азотных, 6кг фосфорных и 3кг калийных удобрений. Известно что для некоторого газона требуется, по меньшей мере 10кг азотных, 20кг фосфорных и 7кг калийных удобрений. Обычный набор стоит 3уе., а улучшенный- 4уе. Какие и сколько наборов нужно купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость.
В соответствии с рекомендациями определим следующие составляющие модели.
1. Неизвестными задачи являются наборы удобрений, которые необходимо купить – набор обычный обозначим х1 и улучшенный х2.
2. Целевой функцией положим стоимость этих наборов, которую необходимо минимизировать
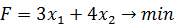
3. Ограничения задачи следуют из необходимости введения определенного количества азотных, фосфорных и калийных удобрений.
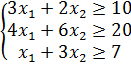
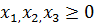
Математическая модель составлена и можно решить задачу средством Поиск решения в Excel.
|
|
|


