 |
Правило исследования функции y=f(x) на экстремум
|
|
|
|
Найти область определения функции f(x).
Найти первую производную функции f '(x).
Определить критические точки, для этого:
найти действительные корни уравнения f '(x)=0;
найти все значения x, при которых производная f '(x) не существует.
Определить знак производной слева и справа от критической точки. Так как знак производной остается постоянным между двумя критическими точками, то достаточно определить знак производной в какой-либо одной точке слева и в одной точке справа от критической точки.
Вычислить значение функции в точках экстремума.
Рассмотрим еще одну теорему, формулирующую достаточное условие существование экстремума с помощью второй производной.
Пусть и существует и непрерывна в некоторой окрестности точки х1.
Теорема (Второе достаточное условие существования экстремума).
Если в точке х = х0 первая производная функции равна нулю (f¢ (x0) = 0), а вторая производная в точке х0 существует и отлична от нуля ( f¢ ¢ (x0)≠ 0 ), то при f¢ ¢ (x0)< 0 в точке x0 функция имеет максимум, и минимум, при f¢ ¢ (x0)> 0.
Замечание. Если f¢ ¢ (x0) = 0, то характер критической точки неизвестен. Для его определения требуется дальнейшее исследование.
Как видим, функция может иметь несколько локальных максимумов и минимумов во внутренних точках своей области определения. Для нахождения оптимума имеет значение понятие глобального экстремума и значения функции на границах области.
Говорят, что функция f(x) имеет в точке x0 глобальный максимум (минимум) на множестве Х, если для всех 
выполняется условие 
Наибольшее и наименьшее значения функции на отрезке.
Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений.
|
|
|
Рассмотрим функцию y=f(x), непрерывную на отрезке [a, b]. Как известно, такая функция достигает своего наибольшего и наименьшего значений, либо на границе отрезка, либо внутри него. Если наибольшее или наименьшее значение функции достигается во внутренней точке отрезка, то это значение является максимумом или минимумом функции, то есть достигается в критических точках.
Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке[a, b]:
Найти все критические точки функции в интервале (a, b) и вычислить значения функции в этих точках.
Вычислить значения функции на концах отрезка при x = a, x = b.
Из всех полученных значений выбрать наибольшее и наименьшее.
Экстремум функции двух переменных.
Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М0(х0, у0) верно неравенство
то точка М0 называется точкой максимума.
Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М0(х0, у0) верно неравенство
то точка М0 называется точкой минимума.
Теорема. (Необходимые условия экстремума).
Если функция z=f(x, y) в точке (х0, у0) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю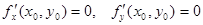 
, либо хотя бы одна из них не существует.
Эту точку (х0, у0) будем называть критической точкой.
Теорема. (Достаточные условия экстремума функции двух переменных).
Пусть в окрестности критической точки (х0, у0) функция z=f(x, y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (х0, у0) значения
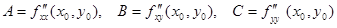. Обозначим
Тогда:
Если ∆ > 0, то в точке (х0, у0) функция z=f(x, y) имеет экстремум, причем, если
A< 0 - максимум, если A> 0 - минимум.
Если ∆ < 0, то в точке (х0, у0) функция z=f(x, y) не имеет экстремума
|
|
|
В случае, если ∆ = 0, вывод о наличии экстремума сделать нельзя. Экстремум может быть, а может и не быть. Необходимы дополнительные исследования.
Условный экстремум.
Условный экстремум находится, когда переменные х и у, входящие в функцию
z = f( x, y), не являются независимыми, т. е. существует некоторое соотношение (условие)
j(х, у) = 0, которое называется уравнением связи.
Имеем задачу – найти экстремум функции z= f( x, y) при условии j(х, у) = 0.
Введем функцию L = f(x, y) + lj(x, y), которая называется функцией Лагранжа.
Таким образом, задача на условный экстремум функции z= f( x, y) свелась к задаче на безусловный экстремум функции L.
Для определения критической точки надо найти все частные производные функции Лагранжа и приравнять их нулю. Получим систему трех уравнений:
Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум. Для этого привлекается условие достаточности.
Пример.
Найти экстремум функции f(x, y) = xy, если уравнение связи:
2x + 3y – 5 = 0
Решение.
Составим функцию Лагранжа и найдем точки экстремумов:
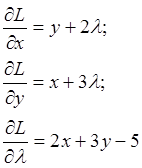
Таким образом, функция имеет экстремум в точке 
, равный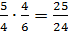 
.
Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа.
Выше мы рассмотрели функцию двух переменных, однако, все рассуждения относительно условного экстремума могут быть распространены на функции большего числа переменных.
Рассмотрим пример задачи, требующей для своего решения нахождения экстремума.
Максимизация производственной функции.
Для производства некоторой продукции используются ресурсы n типов. Затраты ресурсов формально можно представить в виде вектора х=(х1, х2, …, хn), где xi – количество ресурса типа i (i=1, …, n), по экономическому смыслу xi> 0. При неизменной технологии объем произведенной продукции определяется количеством затраченных ресурсов всех типов, следовательно, существует функция f(х1, х2, …, хn), выражающая количество продукции, получаемой при векторе затрат ресурсов (х1, х2, …, хn). Функция f называется в этом случае производственной функцией.
|
|
|
Основное свойство производственных функций – монотонность, означающая, что при увеличении затрачиваемых ресурсов количество продукции увеличивается.
Пусть целью фирмы является максимизация количества производимой продукции. Ограниченность ресурсов или средств на их приобретение является причиной, по которой невозможно производить сколь угодно большое количество продукции. Допустим, фирма покупает ресурсы по фиксированным ценам. Пусть р = (р1, р2, …, рn) – вектор цен где pi ≥ 0 является ценой единицы ресурса i-го типа. Предположим, что суммарные затраты на все ресурсы не должны превышать некоторой пороговой величины d. Тогда вектор ресурсов х=(х1, х2, …, хn) будет допустимым, если общая стоимость ресурсов не будет превосходить d
Алгоритмы оптимизационных задач очень сложны, без применения компьютера их решить весьма проблематично. Программное обеспечение компьютера реализует алгоритмы поиска оптимального решения, которые преобразуют исходные данные в результат.
Метод поиска оптимального решения выбирается исходя из вида целевой функции z и наложенных ограничений. Например, если z линейно зависит от решения х и все ограничения представляют собой линейные неравенства или уравнения, то возникает классическая задача линейного программирования.
Если, исходя из содержательного смысла задачи, ее решения должны быть целыми числами, то это задача целочисленного программирования.
Если критерий оптимальности и (или) ограничения задаются нелинейными функциями, то задача нелинейного программирования, в частности, если указанные функции обладают свойствами выпуклости, то задача выпуклого программирования.
Если в задаче математического программирования имеется переменная времени и критерий эффективности выражается косвенно, через уравнения, описывающие протекание операции во времени, то это динамическое программирование.
Если z или ji зависят от параметра, то параметрическое программирование, если эти функции носят случайный характер, то стохастическое программирование.
|
|
|
По своей содержательной постановке множество других типовых задач исследования операций может быть разбито на ряд классов.
Задачи сетевого планирования и управления рассматривают соотношения между сроками окончания крупного комплекса операций и моментом начала всех операций комплекса. Эти задачи состоят в нахождении минимальной продолжительности комплекса операций, оптимального соотношения величин стоимости и сроков их выполнения.
Задачи массового обслуживания посвящены изучению и анализу систем обслуживания с очередями заявок и состоят в определение показателей эффективности работы систем, их оптимальных характеристик, например, в определение числа каналов обслуживания, времени обслуживания и т. п.
Задача управления запасами состоит в отыскании оптимальных значений уровня запасов и размера заказа. Особенность таких задач заключается в том, что с увеличением уровня запасов, с одной стороны, увеличиваются затраты на хранение, но с другой, уменьшаются потери вследствие возможного дефицита запасаемого продукта.
Задача распределения ресурсов возникает при определенном наборе работ (операций), которые необходимо выполнить при ограничении наличных ресурсов, и требуется найти оптимальной распределение ресурсов между операциями или состав операций.
Задача ремонта и замены оборудования сводится к определению оптимальных сроков, числа профилактических ремонтов и проверок, а также замены оборудования модернизированным.
Задача составления расписания состоит в определении оптимальной очереди выполнения операций на различных видах оборудования
Задача планировки и размещения состоит в определении оптимального числа и места размещения новых объектов с учетом их взаимодействия с существующими объектами и между собой.
Задачи выбора маршрута или сетевые задачи состоят в определение наиболее экономичных маршрутов.
|
|
|
