Распределительные задачи.

Модель распределительной задачи может применяться при рассмотрении практических ситуаций, связанных с управлением запасами, составлением именных графиков, назначением служащих на рабочие места, оборотом наличного капитала.

К этому типу задач относятся транспортная задача и задача о назначениях.

Транспортная модель используется для составления наиболее экономичного плана перевозок одного вида продукции из нескольких пунктов наличия продукции в пункты требования – пункты доставки.

Итак, задача состоит в следующем. Из m пунктов наличия продукции необходимо доставить эту продукцию в требуемых объемах в n пунктов требования. Стоимость перевозки единицы продукции из пункта производства i в пункт потребления j известна и равна значениям 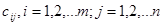. Потребности одного пункта назначения могут удовлетворяться из нескольких исходных пунктов, так же один пункт производства может поставлять товар в несколько пунктов потребления. Необходимо определить объемы продукции, которую следует перевозить из всех исходных пунктов в пункты потребления при минимальных общих транспортных расходах.

Основное предположения транспортной модели состоит в том, что величина расходов на каждом маршруте прямо пропорциональна объему перевозимой продукции.

1. Неизвестными транспортной задачи являются элементы матрицы, образующей объемы перевозки груза из каждого пункта производства в каждый пункт потребления .

2. Целевой функцией являются общие транспортные расходы, связанные с доставкой. Они могут быть выражены в стоимостных единицах или в затратах горючего или единицах пути.

3. В качестве ограничений используются:

· величины, характеризующие объем производства в каждом исходном пункте ;

· величины, характеризующие объем спроса в каждом пункте потребления ;

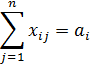
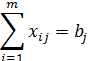
i=1,.., m, j=1, …, n

Математическая модель транспортной задачи составлена и ее можно решить средством Поиск решения в Excel.

Транспортная задача формулируется так, что все грузы из пунктов наличия должны быть доставлены в пункты требования. Это означает, что в задаче объемы вывозимой из пунктов наличия продукции должны равняться объемам продукции, доставленной в пункты требования. Такая задача называется сбалансированной, или закрытой. Однако на практике спрос не всегда равен объему производства, и мы имеем дело с несбалансированной, или закрытой задачей. Однако транспортную модель всегда можно сбалансировать.

Если модель несбалансированная, то надо ввести:

• в случае перепроизводства - фиктивный пункт распределения, при этом стоимость перевозки в i-ый пункт положить равной нулю, или, при необходимости его хранить, равной стоимости складирования, тогда объем «перевозок» груза в j-ый пункт будет равен объему складирования излишков продукции на фабриках.

• в случае дефицита - фиктивный пункт наличия, стоимость перевозки единицы продукции из этого пункта положить равной нулю, или при необходимости уплачивать недопоставку, стоимости штрафов за недопоставку продукции, а объемы «перевозки» будут равны объемам недопоставок продукции в соответствующий пункт распределения.