 |
Рассмотрим пример решения транспортной задачи в Excel.
|
|
|
|
Рассмотрим пример решения транспортной задачи в Excel.
Допустим, что фирма имеет 5 фабрик в пунктах A, B, C, D, E, свои товары она поставляет в 4 центра распределения в городах 1, 2, 3, 4. Ежедневно на фабриках в пунктах A, B, C, D, E производится 15, 55, 12, 18, 17 единиц продукции. Распределительные центры располагаются в городах 1, 2, 3, 4 ежедневно испытывают потребность в товарах 35, 35, 15, 25 единиц продукции.
Стоимость перевозки единицы продукции с фабрик в центры распределения такова:
|
Пункты потребления | ||||
| Предприятия | ||||
| A | 2, 3 | |||
| B | 1, 3 | 2, 5 | ||
| C | 4, 9 | |||
| D | ||||
| E | 2, 1 | 1, 2 | ||
Требуется так запланировать перевозки, чтобы минимизировать суммарные транспортные расходы. Заметим, что данная модель не сбалансирована, то есть суммарный объем произведенной продукции 117 единиц не равен суммарному объему потребностей в этой продукции, равной 110 единиц. Имеется факт перепроизводства продукции, что означает, что часть продукции останется на фабрике. Следовательно, для решения задачи, в этой модели надо ввести фиктивный пункт распределения.
Подготовим данные на листе Excel.
Вводим матрицу коэффициентов целевой функции, элементами которой являются стоимости перевозки единицы груза из одного пункта в другой. Далее отводим диапазон ячеек под неизвестные нашей задачи, то есть под матрицу объемов перевозки грузов, которая и составит оптимальный план задачи перевозок. Можно ввести первоначальные опорные значения объемов перевозки, а можно оставить эти ячейки пустыми.
В ячейку Н3 вводим формулу целевой функции:
=СУММПРОИЗВ(B5: F9; B17: F21).
В ячейки H17: H21 вводим ограничения по объемам производства, являющиеся левыми частями ограничений:
|
|
|
=СУММ(B17: F17)
=СУММ(B18: F18)
=СУММ(B19: F19)
=СУММ(B20: F20)
=СУММ(B21: F21)
В ячейки K17: K21 вводим ограничения по потребностям, являющиеся левыми частями следующей группы ограничений, включая потребности фиктивного пункта:
=СУММ(B17: B21)
=СУММ(C17: C21)
=СУММ(D17: D21)
=СУММ(E17: E21)
=СУММ(F17: F21)
Рядом вводим числовые значения правых частей ограничений.
Вызываем окно Поиск решения и заполняем:
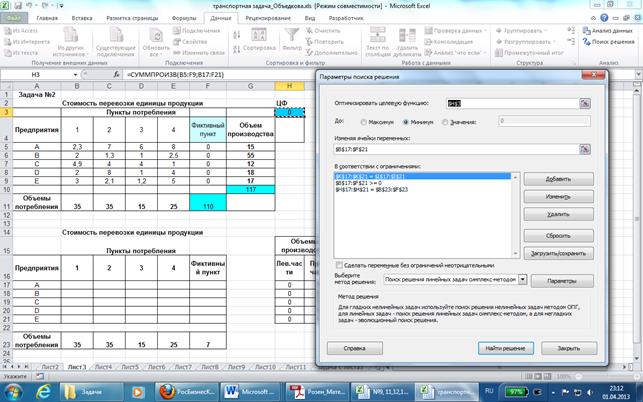
После выполнения получим
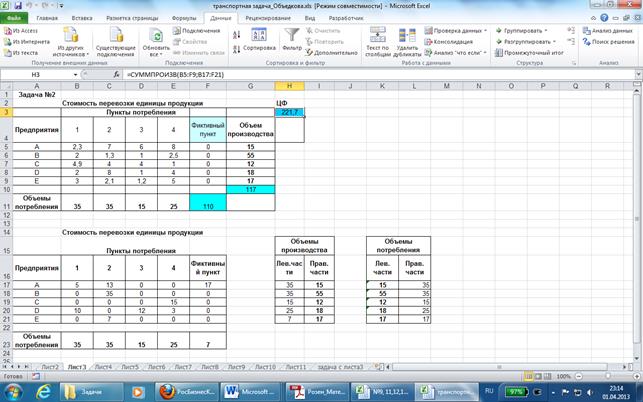
Решение дает матрицу распределения перевозок:
|
Пункты потребления | |||||
| Предприятия | Фиктивный пункт | ||||
| A | |||||
| B | |||||
| C | |||||
| D | |||||
| E | |||||
Наличие поставки в фиктивный пункт 17 единиц продукции означает, что в пункте производства А останутся излишки в размере 17 единиц. Остальная продукция будет развезена в соответствии с полученным планом.
Задача о назначениях
Задача о назначениях относится к распределительным задачам линейного программирования, ее можно считать частным случаем транспортной задачи. Задача о назначениях формулируется, например, при назначении людей на должности или работы, автомашин на маршруты, водителей на машины, при распределении групп по аудиториям, научных тем по научно-исследовательским лабораториям.
Особенность этой задачи состоит в том, что для выполнения каждой работы требуется один и только один ресурс (один человек, одна автомашина), каждый ресурс, в свою очередь, может быть использован на одной и только одной работе. То есть ресурсы не делимы между работами, а работы не делимы между ресурсами.
Математическая модель строится следующим образом.
Будем для определенности считать ресурсом работников, которые назначаются для выполнения определенных работ. Пусть количество работников равно n, а количество работ – m.
Обозначим работников 
( 
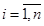), работы - 
( 
).
|
|
|
Тогда неизвестными задачи обозначим 
– работник i выполняет работу j. Неизвестная принимает значения, отражающие факт назначения или неназначения работника на работу :
Если при распределении на работы критерием является качество выполнения, целью задачи будет максимизация функции качества выполнения всех работ. Пусть 
– характеристика качества выполнения работы 
с помощью работника 
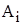. Например, компетентность i-го работника при работе на j-й должности. Тогда ищем максимум целевой функции z(X), выражающей общую (суммарную) характеристику качества выполнения работ.
Если критерием является выполнение всех работ с наименьшими затратами, - стоимость выполнения работником 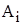работы . Тогда ищется минимум целевой функции z(X), выражающей суммарную стоимость выполнения работ.
Ограничениями задачи является, с одной стороны, тот факт, что один работник выполняет только одну работу, это можно выразить как равенство единице суммы всех работ, выполненных одним работником:
.
С другой стороны, каждая работа должна выполняться только одним работником, то есть, сумма исполнителей одной работы равна единице: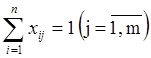 
Матрица задачи о назначениях будет иметь вид:
| Ресурсы, | Работы, | Количество ресурсов | |||
| 
| … | 
| ||
| 
| 
| … | 
| |
| 
| 
| … | 
| |
| … | … | … | … | … | … |
| 
| 
| … | 
| |
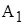
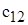
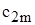
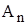
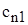
| Количество работ | … |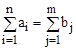 
| |||
|
|
|
