 |
Нахождение рациональных затрат при строительстве трубопроводов и транспортных артерий
|
|
|
|
Требуется проложить путь (трубопровод, шоссе) между двумя пунктами А и В таким образом, чтобы суммарные затраты на его сооружение были минимальные.
Решение. Разделим расстояние между пунктами А и В на шаги (отрезки). На каждом шаге можем двигаться либо строго на восток (по оси X), либо строго на север (по оси У). Тогда путь от А в В представляет ступенчатую ломаную линию, отрезки которой параллельны одной из координатных осей. Затраты на сооружение каждого из отрезков известны в млн р.
Таблица 28 - Исходные данные задачи
У (север) В
А X (восток)
Разделим расстояние от А до В в восточном направлении на 4 части, в северном — на 3 части. Путь можно рассматривать как управляемую систему, перемещающуюся под влиянием управления из начального состояния А в конечное В. Состояние этой системы перед началом каждого шага будет характеризоваться двумя целочисленными координатами х и у. Для каждого из состояний системы (узловой точки) найдем условное оптимальное управление. Оно выбирается так, чтобы стоимость всех оставшихся шагов до конца процесса была минимальна. Процедуру условной оптимизации проводим в обратном направлении, т.е. от точки В к точке А. Найдем условную оптимизацию последнего шага:
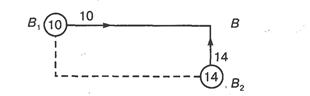
Рисунок 30
В точку В можно попасть из В 1или В 2. В узлах запишем стоимость пути. Стрелкой покажем минимальный путь. Рассмотрим предпоследний шаг.
|
|
|
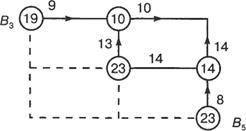
Рисунок 31
Для точки В 3условное управление — по оси X, а для точки В 5— по оси У. Управление для точки В 4 выбираем как min (13 + 10,14 + 14) = min (23,28) = 23, т.е. по оси У.
 |
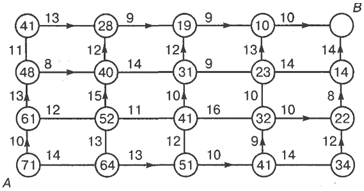Условную оптимизацию проводим для всех остальных узловых точек:
Рисунок 32
Получим
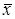опт = (с, с, в, с, в, в, в),
где с — север, в —восток.
Минимальные затраты составляют
10 + 13 + 8 + 12 + 9 + 9 + 10 = 71 млн р.
Если решать задачу исходя из оптимальности на каждом этапе, то решение будет следующим:
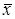=(с, в, в, с, в, с, в). Затраты составят 10 + 12 + 11 + 10 + 9 + 13 + 10 = 75 > 71.
Ответ. Прокладывать путь целесообразно по схеме: с, с, в, с, в, в, в, при этом затраты будут минимальные и составят 7 1млн р.
Задачи для самостоятельного решения
1. Определить оптимальный цикл замены оборудования при следующих исходных данных: Р = 11, s (t) = 0, f (t)= r (t) — u (t), представленных в таблице.
| N | ||||||||||||||
| f (t) |
2.Совет директоров фирмы рассматривает предложения по наращиванию производственных мощностей для увеличения выпуска однородной продукции на трёх предприятиях, принадлежащих фирме. Для расширения производства совет директоров выделяет средства в объеме 150 млн р. с дискретностью 30 млн р. Прирост выпуска продукции на предприятиях зависит от выделенной суммы, его значения представлены предприятиями и содержатся в таблице. Найти распределение средств между предприятиями, обеспечивающее максимальный прирост выпуска продукции, причем на одно предприятие можно осуществить не более одной инвестиции.
| Выделяемые средства, млн р. | Прирост выпуска продукции, млн р. | ||
| Предприятие № 1 | Предприятие № 2 | Предприятие № 3 | |
3.В трех городах предприниматель планирует построить четыре фабрики одинаковой мощности по выпуску обувных изделий, пользующихся спросом. Необходимо разместить предприятия таким образом, чтобы обеспечить минимальные суммарные затраты на их строительство и эксплуатацию. Значения функции затрат gi (x)приведены в таблице.
|
|
|
| x | ||||
| g 1(x)ffi(s) | ||||
| g 2(x) | ||||
| g 3(x) |
4. Требуется проложить шоссе между двумя пунктами А и В таким образом, чтобы суммарные затраты на его сооружение были минимальные.
У (север) В
А X (восток)
Глава VII. СЕТЕВЫЕ МОДЕЛИ
До появления сетевых методов планирование работ, проектов осуществлялось в небольшом объеме. Наиболее известным средством такого планирования был ленточный график Ганта, недостаток которого состоит в том, что он не позволяет установить зависимости между различными операциями.
Современное сетевое планирование начинается с разбиения программы работ на операции. Определяются оценки продолжительности операций, и строится сетевая модель (график), Построение сетевой модели позволяет проанализировать все операции и внести улучшения в структуру модели до начала ее реализации. Строится календарный график, определяющий начало и окончание каждой операции, а также взаимосвязи с другими операциями графика. Календарный график выявляй критические операции, которым надо уделять особое внимание, чтобы закончить все работы в директивный срок. Что касается некритических операций, то календарный план позволяет определить резервы времени, которые можно выгодно использовать при задержке выполнения работ или эффектном применении как трудовых, так и финансовых ресурсов.
Основные понятия сетевой модели
Основные понятия
Сетевая модель — графическое изображение плана выполнения комплекса работ, состоящего из нитей (работ) и узлов (событий), которые отражают логическую взаимосвязь всех операций. В основе сетевого моделирования лежит изображение планируемого комплекса работ в виде графа. Граф — схема, состоящая из заданных точек (вершин), соединенных системой линий. Отрезки, соединяющие вершины, называются ребрами (дугами) графа. Ориентированным называется такой граф, на котором стрелкой указаны направления всех его ребер (дуг), что позволяет определить, какая из двух его граничным вершин является начальной, а какая — конечной. Исследований таких сетей проводится методами теории графов.
|
|
|
Теория графов оперирует понятием пути, объединяющим последовательность взаимосвязанных ребер. Контур означает такой путь, у которого начальная вершина совпадает с конечной. Сетевой график — это ориентированный граф без контуров. В сетевом моделировании имеются два основных элемента — работа и событие [10].
Работа — это активный процесс, требующий затрат ресурсов, либо пассивный (ожидание), приводящий к достижению намеченного результата.
Фиктивная работа — это связь между результатами работ (событиями), не требующая затрат времени и ресурсов.
Событие — это результат (промежуточный или конечный) выполнения одной или нескольких предшествующих работ.
Путь — это любая непрерывная последовательность (цепь) работ и событий.
Критический путь — это путь, не имеющий резервов и исключающий самые напряженные работы комплекса. Работы, расположенные на критическом пути, называют критическими. Все остальные работы являются некритическими (ненапряженными) и обладают резервами времени, которые позволяют передвигать сроки их выполнения, не влияя на общую продолжительность выполнения всего комплекса работ.
При построении сетевых моделей необходимо соблюдать следующие правила.
1. Сеть изображается слева направо, и каждое событие с большим порядковым номером изображается правее предыдущего. Общее направление стрелок, изображающих работы, также в основном должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером.
|
|
|
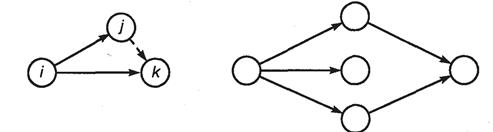
а) б)
Рисунок 32
2. Два соседних события могут объединяться лишь одной работой. Для изображения параллельных работ вводятся промежуточное событие и фиктивная работа (рис.32 а).
 |  | ||
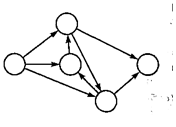3. В сети не должно быть тупиков, т.е. промежуточных событий, из которых не выходит ни одна работа (рис. 32 б).
а) б)
Рисунок 33
10. В сети не должно быть промежуточных событий, которым не предшествует хотя бы одна работа (рис. 33 а).
В сети не должно быть замкнутых контуров, состоящих из взаимосвязанных работ, создающих замкнутую цепь (рис. 33 б). Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события, которому дается номер 1. Из исходного события 1 вычеркивают все исходящие из него работы, на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию дается номер 2. Затем вычеркивают работы, выходящие из события 2, и вновь находят на оставшейся части сети событие, в которое не входит ни одна работа, ему присваивается номер 3, и так продолжается до завершающего события. Пример нумерации сетевого графика показан на рис. 34.
Продолжительность выполнения работ устанавливается на основании действующих нормативов или по экспертным оценкам специалистов. В первом случае временные оценки являются детерминированными (однозначными), во втором — стохастическими (вероятностными).
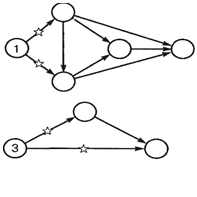
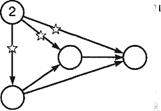
Рисунок 34
Рассмотрим в качестве примера программу создания нового бытового прибора, пользующегося спросом у населения. Необходимые данные приведены в таблице 28.
На основании данных таблицы построим сетевой график создания прибора с учетом вышеизложенных рекомендаций (рис. 35).
 |
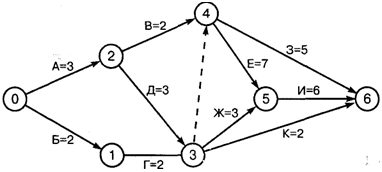Рисунок 35
|
|
|
