 |
Обоснование привлекательности проекта по выпуску продукции
|
|
|
|
Для финансирования проектов по строительству и наладке изготовления конкурентоспособной продукции в большинстве случаев фирмам требуются инвестиции. Включение в проект материалов с оптимизацией сетевых моделей в части обоснования сроков возврата инвестиций делает проект более привлекательным и способствует принятию инвестором положительного решения.
Пример 46. Предприятие решило для улучшения финансового состояния наладить выпуск конкурентоспособной продукции (мороженого). Для переоборудования цеха (участка) под выпуск этой продукции необходимо выполнить:
1) подготовку технического задания на переоборудование участка (30 дн.);
2) заказ и поставку нового оборудования (60 дн.);
3) заказ и поставку нового электрооборудования (50 дн.);
4) демонтаж старого и установку нового оборудования (90 дн.);
5) демонтаж старого и установку нового электрооборудования
(80 дн.);
6) переобучение персонала (30 дн.);
7) испытания и сдачу в эксплуатацию оборудования для производства мороженого (20 дн.).
Ожидается, что производительность после ввода новой линии составит 20 т мороженого в смену. Прибыль от реализации 1 т продукции составит 0,5 тыс. р. в смену. Деньги на покупку и переоборудование участка в размере 2 000 тыс. р. взяты в банке под 20% годовых (из расчета 1500 тыс. р. на закупку оборудования и 500 тыс. р. на работы по демонтажу старого оборудования и установке нового оборудования). Затраты на проведение работ в нормальном и максимальном режимах указаны в таблице 31. Определить, через какое время может быть возвращен кредит в банк.
Таблица 31 - Затраты на проведение работ в нормальном и максимальном режимах.
| Работа | Нормальный режим | Максимальный режим | ||
| Продолжительность, дн | Затраты,тыс. р. | Продолжительность, дн. | Затраты, тыс. р. | |
| Итого |
Решение. 1. Составим график проведения работ по пуску новой линии:
|
|
|
Рисунок 43
На проведение переоборудования необходимо
30 + 60 + 50 + 90 + 80 + 30 + 20 = 360 дн.
2. График можно улучшить, выполняя некоторые работы параллельно. Получим график (рис. 44).
Рисунок 44
На этом графике обозначены работы:
0,1 — подготовка технического задания;
1.2 — заказ и поставка нового оборудования;
1.3 — заказ и поставка нового электрооборудования;
2.4— установка нового оборудования;
3,4 — установка нового электрооборудования;
1.4 — переобучение персонала;
4.5— сдача в эксплуатацию новой линии.
По графику путь (0,1), (1,2), (2,4), (4,5) имеет продолжительность 200 дн.; (0,1), (1,3), (3,4), (4,5) — 180 дн.; (0,1), (1,4), (4,5)—80дн.
Критическим путем графика является путь, на котором находятся работы (0,1), (1,2), (2,4), (4,5) продолжительностью 30+60+90+20=200 дн.
График улучшился на 360 — 200 = 160 дн.
Определим, через какое время после начала выпуска мороженого может быть возвращен кредит в банк.
Через 200 дн. после начала работ предприятие истратит 1500 тыс. р. на приобретение оборудования (согласно условию примера) и 265 тыс. р. на его установку и сдачу в эксплуатацию (см. табл. 31, столбец "Затраты" при нормальном режиме).
В наличии у предприятия останется 2000-1500-265=235 тыс. р.
Построим графики изменения кредита в зависимости от времени получения прибыли предприятием — от выпуска мороженого (рис. 45).
Рисунок 45
Для построения графика изменения кредита в зависимости от времени составим уравнение. Через 360 дн. после выдачи банком кредита под 20% годовых долг предприятия составит 2400 тыс. р. Поэтому известны две точки этой прямой: А(0, 2000), В(360,2400). Согласно уравнению прямой, проходящей через две точки:
|
|
|
(у - у А)/(у В - у А)= (х - х А)/(х В - х А),
(у- 2000)/(2400-2000)=(х- 0)/(360-0).
Решая уравнение, получим 10 х - 9 у + 18000 = 0. (69)
Найдем уравнение прибыли предприятия. Известно, что через 200 дн. после начала работ у предприятия осталось от кредита 235 тыс. р. Через 100 дн. после начала выпуска продукции предприятие получит прибыль
0,5(тыс. р.) · 20(т) · 100(дн.) = 1000 тыс. р.
и у него будет в наличии 1000 + 235 = 1235 тыс. р.
Таким образом, для нахождения уравнения прибыли имеем две точки: С(200,235), D(300,1235). Тогда
(у - у С) / (у D - у С) = (х - x C) / (xD - х С),
(у - 235)/(1235 - 235) = (х - 200)/(300 - 200), (70)
10 х-у- 1765 = 0.
Решая совместно уравнения (69) и (70), определим время, когда кредит может быть возвращен в банк:
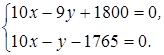
Откуда получаем у = 2471, х = 423,6 ≈ 424 дн.
3. График выполнения работ может быть сжат за счет выполнения некоторых операций в максимально интенсивном режиме.
Вычислим наклоны кривой "затраты-продолжительность" для каждой операции. Результаты расчетов даны в табл. 32.
Учитывая наклоны кривой, производим сжатие операций (0,1), (2,4), (3,4), (4,5), получим сетевой график (рис. 46).
Таблица 32 - Наклоны кривой "затраты-продолжительность".
| Операция | Наклон |
| 0,1 | |
| 1,2 | 1,3 |
| 1,3 | |
| 2,4 | 1,5 |
| 3,4 | 0,7 |
| 1,4 | |
| 4,5 | 1,7 |
Рисунок 46
Новый график имеет 2 критических пути: (0,1), (1,2), (2,4), (4,5) и (0,1), (1,3), (3,4), (4,5) с продолжительностью 157дн.
Таким образом, критический путь сокращен с 200 до 157 дн., а это означает, что предприятие начнет производить мороженое через 157 дн. после начала работ.
Определим, сколько предприятию придется заплатить за"сжатие" критического пути (см. табл. 31):
(0,1): 30 - 20 = 10 тыс. р.;
(1,2): 60 - 40 = 20 тыс. р.;
(2,4): 100 - 70 = 30 тыс. р.;
(3,4): 70-60 = 10 тыс. р.;
(4,5): 25 - 20 = 5 тыс. р.
Таким образом, "сжатие" работ (0,1), (1,2), (2,4), (3,4), (4,5) обойдется предприятию в 10 + 20 + 30 + 10 + 5 = 75 тыс. р.
График изменения кредита в зависимости от времени остается прежним (см. рис. 46). Его вид определяет уравнение 10 х - 9 у + 18000 = 0.
Найдем уравнение прибыли.
Через 157 дн. после начала работ у предприятия осталось от кредита
2000 - 1500 - 265 - 75 = 160 тыс. р.
Через 100 дн. после начала выпуска продукции предприятие получит прибыль
20(тыс. р.) · 0.5(тыс. р.) · 100(дн.) = 1000 тыс. р.,
и у него будет в наличии 1000 + 160 = 1160 тыс. р.
Таким образом, для нахождения уравнения прибыли предприятия имеем две точки: С ' (157,160) и D'(257,1160).
|
|
|
Согласно уравнению прямой, проходящей через 2 точки, получим
(у - у С ') / (у D'- у С') = (х - x C ') / (xD ' - х С '),
(у - 160)/(1160 - 160) = (х - 157)/(257 - 157), (71)
10 х-у- 1410 = 0.
Решая совместно уравнения (69) и (71), определим время, когда кредит может быть возвращен в банк:
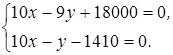у = 2426,25, х = 383,6 ≈ 384 дн.
Таким образом, через 384 дн. предприятие может вернуть кредит в банк. По сравнению с предыдущим случаем (см. п. 2) предприятие вернет в банк деньги раньше на 424—384 = 40 дн.
При нормальном режиме работ критический путь составляет 200 дн., стоимость работ — 265 тыс. р.
Критический путь уменьшен до 157 дн., минимальная стоимость работ составляет 265+75 = 340 тыс. р, при максимальном режиме.
Минимизация сети
Задача минимизации сети состоит в нахождении ребер, соединяющих все узлы сети и имеющих минимальную суммарную длину (рис. 47).
Рисунок 47
На ребрах, соединяющих узлы 1, 2, 3, указаны длины. Узел 3 соединен с узлами 1 и 2 минимальной длиной 4 + 6 = 10. Если соединить узлы 1 и 2, то возникает цикл и получающаяся, сеть не будет минимальной. Отсутствие циклов в минимальной сети дало ей название "минимальное дерево-остов".
Алгоритм решения
Начнем с любого узла и соединим его с ближайшим узлом сети. Соединенные два узла образуют связное множество, а остальные — несвязное. Далее в несвязном множестве выберем узел, который расположен ближе других к любому из узлов связного множества. Скорректируем связное и несвязное множества и будем повторять процесс до тех пор, пока в связное множество не попадут все узлы сети. В случае одинаково удаленных узлов выберем любой из них, что указывает на неоднозначность (альтернативность) "минимального дерева-остова".
 |
Пример 47. Телевизионная фирма планирует создание кабельной сети для обслуживания 5 районов-новостроек. Числа на ребрах указывают длину кабеля (рис. 48а). Узел 1 — телевизионный центр. Отсутствие ребра между двумя узлами означает, что соединение соответствующих новостроек либо связано с большими затратами, либо невозможно.
|
|
|
б)
Рисунок 48
Найти такое соединение кабелем районов-новостроек, чтобы длина его была минимальной.
Решение. Минимальная длина кабеля: 1 + 3+4+3 + 5 = 16 (рис. б).
Пример 48. На рис. 49 указаны длины коммуникаций, связывающих 9 установок по добыче газа в открытом море с расположенным на берегу приемным пунктом. Поскольку скважина 1 расположена ближе всех к берегу, она оснащена необходимым оборудованием для перекачки газа, идущего с остальных скважин в приемный пункт.
Построить сеть трубопровода, соединяющего все скважины с приемным пунктом и имеющего минимальную общую длину труб.
 |
Рисунок 49
Рисунок 50
Решение. Минимальная длина труб: 5 + 6 + 4 + 3 + 7 + 5 + 6 + 5 = 41 (рис. 50).
|
|
|
