Нахождение кратчайшего пути

Задача состоит в нахождении связанных между собой дорог на транспортной сети, которые в совокупности имеют минимальную длину от исходного пункта до пункта назначения.

Введем обозначения:

d_ij — расстояние на сети между смежными узлами i и j;

U_j — кратчайшее расстояние между узлами i и j, U ₁= 0.

Формула для вычисления U_j

Из формулы следует, что кратчайшее расстояние U_j до узла j можно вычислить лишь после того, как определено кратчайшее расстояние до каждого предыдущего узла i, соединенного дугой с узлом j. Процедура завершается, когда получено U_i последнего звена.

Определить кратчайшее расстояние между узлами 1 и 7 (рис. 51).

Рисунок 51

Решение. Найдем минимальные расстояния:

U ₁=0,

U ₂= U ₁+ d ₁₂= 0 + 2 = 2,

U ₃ = U ₁+ d ₁₃ = 0 + 4 = 4,

U ₄ = min{ U ₁+ d ₁₄; U ₂ + d ₂₄; U ₃ + d ₃₄ } = min{0 + 10; 2 + 11; 4 + 3} = 7,

U ₅= min{ U ₂ + d ₂₅; U ₄ + d ₄₅}= min{2 + 5; 7 + 8} = 7,

U ₆ = min{ U ₃+ d ₃₆; U ₄+ d ₄₆} = min{4 + 1; 7 + 7} = 5,

U ₇ = min{ U₅ + d ₅₇, U₆ + d ₆₇}= min{7 + 6; 5 + 9} = 13.

Минимальное расстояние между узлами 1 и 7 равно 13, а соответствующий маршрут: 1-2-5-7.

 

Задача замены автомобильного парка

Фирма по прокату автомобилей планирует замену автомобильного парка на очередные 5 лет. Автомобиль должен проработать не менее 1 года, прежде чем фирма поставит вопрос о его замене. На рис. 52 приведены стоимости замены авто­мобилей (усл. ед.), зависящие от времени замены и количества лет, в течение которых автомобиль находился в эксплуатации.

Рисунок 52

Определить план замены автомобилей, обеспечивающий при этом минимальные расходы.

Решение. Найдем минимальные расстояния:

U ₁ = 0,

U ₂ = U ₁ + d ₁₂= 0 + 4 = 4,

U₃ = min { U ₁ + d ₁₃; U ₂+ d ₂₃} = min{0 + 5,4; 4 + 4,3} = 5,4,

U ₄ = min{ U ₁ + d ₁₄; U ₂+ d ₂₄; U ₃+ d ₃₄} = min{0+9,8; 4+6,2; 5,4+4,8} = 9,8,

U ₅= min{ U ₁ + d ₁₅; U ₂+ d ₂₅ ; U ₃ + d ₃₅; U ₄ + d ₄₅} =

= min{0 + 13,7; 4 + 8,1; 5,4 + 7,1; 9,8 + 4,9} = 12,1.

Кратчайший путь 1-2-5 со стоимостью 12,1 усл. ед. Это означает, что каждый автомобиль заменяется через 2 года, а через 5 — списывается.

Задачи для самостоятельного решения

1. Составить сетевой график выполнения работ и рассчи­тать временные параметры по данным, представленным в табл.

Содержание работы	Обозна­чение	Предыду­щая работа	Продолжи­тельность, дн.
Составление сметы	а 1
Заказ и доставка оборудования	а 2	a1
Распределение кадров	аз	a1
Установка оборудования	а 4	a2
Подготовка кадров	а 5	a3
Оформление торгового зала	а 6	a4
Доставка товаров	а 7	a5
Заказ и получение ценников	a 8	a5
Заказ и получение формы	а 9	a5
Выкладка товаров	а 10	a6, a7
Заполнение ценников	а 11	a5
Генеральная репетиция	а 12	a8, a10, a 11

2. Постройте график работ, определите критический путь и стоимость работ при нормальном режиме, критический путь и минимальную стоимость работ при максимальном режиме. Исходные данные указаны в табл.

	Нормальный режим работ	Максимальный режим работ
Операция	Продолжи­тельность, дн.	Стоимость, ден. ед.	Продолжи­тельность, дн.	Стоимость, ден. ед.
1,2
1,3 1,4	2-3 3-4	50 - 60 60 - 80	1- 2 2 -3	70 – 80 80-100
2,4
2,6
3,4
3,5
4,6
5,6

3. Постройте график работ, определите критический путь и стоимость работ при нормальном режиме, критический путь и минимальную стоимость работ при максимальном режиме. Необходимые исходные данные приведены в табл.

 

	Нормальный режим работ	Максимальный режим работ
Операция	Продолжи­тельность, дн.	Стоимость, ден. ед.	Продолжи­тельность, дн.	Стоимость, ден. ед.
1,2
1,3
1,4
2,5
2,6
3,6
4,7
5,7
6,7

ТЕСТ ДЛЯ САМОКОНТРОЛЯ

1) Среди данных транспортных задач

Мощность поставщиков	Мощность потребителей

Мощность поставщиков	Мощность потребителей

Мощность поставщиков	Мощность потребителей

Мощность поставщиков	Мощность потребителей

Закрытыми являются…

1. 4

2. 1

3. 2

4. 3

 

2) Укажите, какой из разделов математики не входит в раздел высшей математики под названием «Математическое программирование»?

 

1. линейное программирование;

2. алгоритмизация и программирование;

3. нелинейное программирование;

4. динамическое программирование.

 

3) Построение математической модели экономической задачи не включает следующие этапы:

 

1. составление системы ограничений;

2. выбор целевой функции;

3. выбор метода вычисления данной задачи;

4. выбор переменных задачи.

 

4) Для данной целевой функции укажите систему ограничений F(X)= 2 x ₁+4 x₂ → max:

1. ;

2. ;

3.

4.

 

5) Симплексный метод решения задач линейного программирования - это…

 

1. метод позволяющий проверить, является ли данное решение экономической задачи опорным.

2. метод целенаправленного перебора опорных решений задачи линейного программирования. Он позволяет за конечное число шагов расчета либо найти оптимальное решение, либо установить, что оптимального решения не существует.

3. метод увеличения (уменьшения) значения целевой функции в точках линии уровня. Если линию уровня перемещать параллельно начальному положению в направлении нормали, то функция достигает максимального значения, в противоположном направлении - минимального.

4. метод, который позволяет построить опорное решение, достаточно близкое к оптимальному, так как использует матрицу стоимостей задачи. Он состоит из ряда однотипных шагов, на каждом из которых заполняется только одна клетка таблицы, соответствующая стоимости 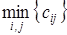и исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель).

 

6) Указать не существующий цикл:

 

·

 

 

·

 

·

 

1. 4

2. 2

3. 1

4. 3

 

 

7) Какой из методов прикладной математики чаще других применяется при решении задач:

1. табличный.

2. симплексный;

3. графический;

4. аналитический;

 

8) Для данной целевой функции укажите систему ограничений F(X)= 3 x ₁+4 x₂ → max:

1. ;

2. ;

3.

4.

 

9) Укажите для данной задачи F(X)= 2 x ₁+4 x₂ →min,

целевую функцию двойственной к ней задачи:

 

1. Z (y)=12 у ₁+9 у ₂+12 у ₃→min

2. Z (y)=12 у ₁+9 у ₂+12 у ₃→mах

3. Z (х)=12 х ₁+9 х ₂+12 х ₃→min

4. Z (y)=-12 у ₁-9 у ₂-12 у ₃→min.

10) Теория игр представляет собой ….

1. математическую модель экономической задачи;

2. математическую обработку игровых ситуаций;

3. математическую теорию конфликтных ситуаций;

4. математическую интерпретацию различных комбинаций.

 

11) Если нижняя цена игры равна верхней, то ….

1. игра не имеет решения;

2. цена игры равна единице;

3. их общее значение называется чистой ценой игры;

4. цена игры называется минимаксной.

 

12) Верхняя цена матричной игры, заданной платежной матрицей , равна…

1. 3

2. 4

3. 5

4. 1

 

13) Нижняя цена матричной игры, заданной платежной матрицей равна…

1. 1

2. 4

3. 3

4. 5

 

14) Сетевая модель - это …

 

1. построение линий и графиков;

2. графическое изображение системы ограничений;

3. графическая интерпретация задачи математического программирования;

4. графическое изображение плана выполнения комплекса работ, состоящего из нитей и узлов, которые отражают логическую взаимосвязь всех операций.

 

15) Теория графов оперирует понятием….

1. работы;

2. событием;

3. пути;

4. графика.

 

16) Для сетевого графика, Изображенного на рисунке:

Длина критического пути равна…

1. 16

2. 18

3. 15

4. 49

 

17) Динамическое программирование — один из разделов оптимального программирования, в котором ……

 

1. программирование принятия решения и управления;

2. работа по принятию решения и управления может быть разбита на отдельные этапы (шаги);

3. решение и управление не может быть разбиты на отдельные этапы (шаги);

4. процесс принятия решения и управления может быть разбит на отдельные этапы (шаги).

 

18) Уравнение описывает N -стадийный процесс, а —

 

1. стадийный;

2. первый;

3. начальный;

4. одностадийный.

 

19) Условную оптимизацию проведем для всех узловых точек:

Тогда оптимальное решение получим:

1. 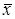_опт = (в, в, в, с, с, в, в);

2. 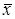_опт = (с, с, в, с, в, в, в);

3. 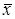_опт = (в, с, в, с, в, в, с);

4. 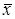_опт = (с, в, в, с, с, в, в).

 

20) На какие классы, с точки зрения методов, можно разделить задачи нелинейной оптимизации?

1. с глобальным и локальным оптимизмом;

2. безусловной и условной оптимизации;

3. безусловной и многокритериальной оптимизации;

4. с экстремумом и без экстремума.

 

21) Почему необходимо знать методы решения задач безусловной оптимизации, если они на практике встречаются крайне редко?

1. методы их решения хороши в теории;

2. методы их решения наглядны и позволяют лучше понять практическую задачу;

3. методы их решения служат основой для отыскания оптимизма практических задач;

4. методы их решения обладают хорошей сходимостью.

 

22) Для чего используется метод множителей Лагранжа при условной оптимизации?

1. для преобразования задачи условной оптимизации в задачу безусловной оптимизации;

2. для замены задачи условной оптимизации задачей безусловной оптимизации;

3. для преобразования задачи безусловной оптимизации в задачу условной оптимизации;

4. для замены задачи безусловной оптимизации задачей условной оптимизации.

 

23) Укажите функцию Лагранжа для следующей системы

 

24) При решении задач нелинейного программирования для целевой функции необходимо определить ……

 

1. глобальный максимум или глобальный минимум;

2. условный максимум или условный минимум;

3. оптимальное решение;

4. наибольшее значение или наименьшее значение.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. Абрамов, Л.M. Математическое программирование. Теория выпуклого программирования / Л.M. Абрамов, В.Ф. Капустин ― СПб: Изд-во Санкт-Петербургского университета, 2001г.- 264 с.
2. *Акулич, И.Л. Математическое программирование в примерах и задачах: учебное пособие для вузов / И.Л. Акулич. – М.: Высшая школа, 1993.- 336 с.
3. Аронович, А.Б. Сборник задач по исследованию операций / А.Б. Аронович, М.Ю. Афанасьев, Б.П. Суворов — М.: Изд-во МГУ, 1997.-256 с.
4. Баумоль, У. Экономическая теория и исследование операций / У. Баумоль. — М.: Прогресс, 1965. - 496 с.

5. Булгакова М.В. Математическое моделирование экономических процессов: учебное пособие / М.В. Булгакова.- Челябинск: МОУ ВПО ЮУПИ, 2010. – 115 с.

1. *Исследование операций / Е.С. Вентцель. — М: Советское радио, 1972. ―552 с.
2. Исследование операций: учебник: в 2 т. / под ред. Дж. Моудер, С. Элмаграби. — М.: Мир, 1981. ― Т. 1. ― Гл. 3. - 712 с.
3. Калихман, И.Л. Линейная алгебра и программирование / И.Л. Калихман. — М.: Высш. шк.,1967.- 432 с.
4. Карасев, А.И. Курс высшей математики для экономических вузов. Ч.II. Теория вероятностей и математическое программирование. Линейное программирование: учеб. пособие для студентов вузов / А.И. Карасев, З.М. Аксютина, Т.И. Савельева.― М.: Высш. школа, 1982.-356 с.
5. Косоруков, О.А. Исследование операций: учебник / Косоруков О.А., Мищенко А.В. // Под общ. ред. Н.П. Тихомирова. – М.: Издательство «Экзамен», 2003.- 448 с.
6. *Красс, М.С. Математика для экономистов / М.С. Красс, Б.П. Чупрынов. – СПб.: Питер, 2004.- 464 с.
7. *Кремер, Н.Ш. Исследование операций в экономике / Н.Ш. Кремер— М.: Банки и биржи, 1997.-407 с.
8. Кузнецов, Ю.Н. Математическое программирование / Ю.Н. Кузнецов, В.И. Кузубов, А.Б. Волощенко ― М.: Высш. шк., 1980.-300 с.
9. Линейное и нелинейное программирование / Под ред. проф. И.Н. Ляшенко. — Киев: Выща шк., 1975.-327 с.
10. Элементы линейного программирования: учебно-методическое пособие / М.В. Булгакова. ― Челябинск: Изд-во ЧВВКУ, 2007.-84 с.
11. Матвеев, В.И. Курс линейного программирования для экономистов: учеб. пособие / В.И. Матвеев, Р.В. Сагитов, В.Г. Шершнев— М.: Менеджер, 1998.-374 с.
12. Математика в экономике: учебник: в 2-х ч. Ч.1 / А.С.Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандра. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2003. -540 с.
13. Математика в экономике: учебник: в 2-х ч. Ч.2 / А.С.Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандра. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2003.-560 с.
14. Монахов, В.М. Методы оптимизации / В.М. Монахов, Э.С. Беляева, М.Я. Краснер. ― М.: Просвещение, 1978.-176 с.
15. Муртаф, Б. Современное линейное программирование / Б. Муртаф — М.: Мир, 1984.-224 с.
16. *Общий курс высшей математики для экономистов: учебник / под ред. В.И. Ермакова. ― М.: ИНФА-М, 2002. -656 с.
17. Gass S.I. Linear Programming: Methods and Applications. — N.Y.: McGraw-Hill, 1985.-532 с.
18. Hadley G. Linear Programming. Reading, Mass: Addison-Weslcy Pub. Co, 1962.-520 с.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

Основная литература:

^1. *Замков, О.О. Математические методы в экономике / О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемных. — М.: Дело и Сервис, 2004. — 365 с.

^2. * Кремер, Н.Ш. Высшая математика для экономистов / 3-е изд. — М.: ЮНИТИ-ДАНА, 2008. — 479 с.

^3. * Кремер, Н. Ш. Математика для экономистов: от Арифметики до Эконометрики [Текст]: учебно-справочное пособие для вузов / Н. Ш. Кремер, Б. А. Путко, И. М. Тришин; под ред. Н. Ш. Кремера. — 2-е изд., перераб. и доп. — М.: Юрайт, 2011. — 646 с.

^4. *Малыхин, В.И. Математика в экономике / В.И. Малыхин. — М.: ИНФРА-М, 2003. — 355 с.

^5. *Практикум по высшей математике для экономистов: Учеб. Пособие для вузов/ Кремер.Н.Ш., Тришин И.М., Путко Б.А. и др. – М.: ЮНИТИ-ДАНА, 2005. — _ 423 с.

 

Дополнительная литература:

^6. Виленкин, И.В. Высшая математика для студентов экономических, технических, естественно-научных специальностей / И.В. Виленкин.- Ростов н/Д: Феникс, 2005.- 414 с.

^7. Косоруков, О.А. Исследование операций: учебник для вузов/ О.А. Косоруков, А.В. Мищенко; Под ред. Н.П. Тихомирова. – М.: Экзамен, 2003. – 446 с.

^8. Кочович, Е. Финансовая математика: с задачами и решениями / Е. Кочович.- М.: Финансы и статистика, 2004.-384 с.

^9. Лагоша, Б.А. Оптимальное управление в экономике: учебное пособие для вузов/ Б.А. Лагоша. – М.: Финансы и статистика, 2003. – 192 с.

^10. Солодовников, А.С. Математика в экономике. В 2-х частях. Ч.1: учебник для вузов/ А.С. Солодовников, В.А. Бабайцев, А.В. Браилов. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2003. – 348 с.

^11. Солодовников, А.С. Математика в экономике. В 2-х частях. Ч.2: учебник для вузов/ А.С. Солодовников, В.А. Бабайцев, А.В. Браилов. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2003. – 560 с.

^12. Шипачев, В.С. Основы высшей математики: учебное пособие для вузов/ В.С. Шипачев, под ред.А.Н. Тихонова.- М.: Высшая школа, 2002. – 479 с.

 

 

⇐ Предыдущая23242526272829303132

Поделиться:

Воспользуйтесь поиском по сайту: