 |
Тема 1.2: Кинематика. Криволинейное движение. Вращение тела вокруг неподвижной оси.
|
|
|
|
КАМЫШИНСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ)
ВОЛГОГРАДСКОГО ГОСУДАРСТВЕННОГО ТЕХНИЧЕСКОГО УНИВЕРСИТЕТА
КАФЕДРА «ФИЗИКА»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям
по дисциплине
«Физика»
часть I
РПК «Политехник»
Волгоград
УДК
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПО ДИСЦИПЛИНЕ «ФИЗИКА». Часть I: Методические указания / сост.
С.А. Ковалёва; Волгоград. Гос. Техн. Ун-т. – Волгоград, 2005. - с.
Рассматривается материал относящийся к разделам «Механика», «Молекулярная физика» и «Термодинамика». Приведен в компактном виде теоретический материал соответствующих разделов, а также типовые задачи и задачи, предложенные для самостоятельного решения.
Предназначены в помощь студентам, обучающимся по направлениям 551200, 552900, 552800.
Илл. Табл. Библ. Назв.
Рецензент к.т.н. доцент Гнедов Ю.А.
Печатается по решению редакционно-издательского совета Волгоградского государственного технического университета.

ВВЕДЕНИЕ
Данные методические указания являются пособием для проведения практических занятий по дисциплине «Физика» (часть I).
Целью данного пособия является описание методики проведения практических занятий по следующим разделам физики: «Механика», «Молекулярная физика» и «Термодинамика». Каждое практическое занятие рассчитано на 2 аудиторных часа. К каждому практическому занятию отдельно составлен план проведения занятия с указанием цели занятия; в компактном виде приведён теоретический материал; рассмотрены типовые задачи с их решениями.
Тема 1.1 Кинематика. Кинематическое уравнение движения. Скорость. Ускорение. Уравнение траектории.
|
|
|
I. Цель практического занятия:
- Закрепить и углубить знание теоретических вопросов, основных понятий и формул кинематики.
- Учиться применять полученные знания для решения задач по данной теме.
II. Расчёт учебного времени:
| Содержание занятия | Время (мин.) |
Вступительная часть:
Объявление темы и цели занятия.
Контрольный опрос:
|
Контрольный опрос
1. Ур-я: x=x(t); y=y(t); z=z(t); или 
2. Вектор средней скорости: < 
Средняя скорость равномерного движения: < 
3. Мгновенная скорость: 
4. 
5. Среднее ускорение: 
6. Мгновенное ускорение: 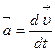
7. Уравнение равнопеременного движения:
8. 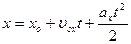 ;
; 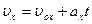
Основная часть
Пример №1 Тр.№1.3
Два автомобиля, выехав одновременно из одного пункта, движутся прямолинейно в одном направлении. Зависимость пройденного ими пути задаётся уравнениями s1=At+Bt2 и s2=Ct+Dt2+Ft3. Определить относительную скорость U автомобилей.
Решение
Если точка движется по прямой в одном направлении, то x совпадает с s и уравнение движения может быть записано в виде 
Определим зависимость пути второго автомобиля относительно первого:
S=S1-S2=(A-B)t+(B-D)t2-Ft3
Тогда скорость движения второго автомобиля относительно первого будет равна:
U= 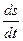 =(A-C)+2(B-D)t-3Ft2.
=(A-C)+2(B-D)t-3Ft2.
Пример №2 Тр.№1.6
Студент проехал половину пути на велосипеде со скоростью 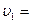 16 км/ч. Далее половину оставшегося времени он ехал со скоростью
16 км/ч. Далее половину оставшегося времени он ехал со скоростью  12 км/ч, а затем до конца пути шёл пешком со скоростью
12 км/ч, а затем до конца пути шёл пешком со скоростью
|
|
|
 5 км/ч. Определить среднюю скорость движения студентов на всём пути.
5 км/ч. Определить среднюю скорость движения студентов на всём пути.
Дано:
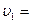 16 км/ч 16 км/ч
 12 км/ч 12 км/ч
 5 км/ч 5 км/ч

| Решение: 
 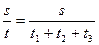 Определим время прохождения первой половины
пути:
Определим время прохождения первой половины
пути:  . По условию: s2+s3= . По условию: s2+s3=  , а t2=t3.
Время прохождения второго и третьего участников
пути: , а t2=t3.
Время прохождения второго и третьего участников
пути:
 и и  Следовательно:
Следовательно:  Решая эту систему получаем: Решая эту систему получаем:
 и и  таким образом
таким образом  тогда средняя скорость на всём пути:
тогда средняя скорость на всём пути:

 км/ч. км/ч.
|
 ? ?
|
Пример №3: Тр.№1.7
В течение времени 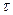 скорость тела задаётся уравнением вида
скорость тела задаётся уравнением вида 
 Определить среднюю скорость за промежуток времени
Определить среднюю скорость за промежуток времени 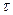 .
.
Решение
По определению  ; для неравномерного движения путь можно определить по формуле:
; для неравномерного движения путь можно определить по формуле:  ,
,
тогда: 
Пример № 4: Тр.№1.18
Зависимость пройденного телом пути от времени задаётся уравнением  (А=6 м, В=3 м/с, С=2 м/с2,
(А=6 м, В=3 м/с, С=2 м/с2,
D=1 м/с3). Определить для тела в интервале времени от  =1 c до
=1 c до  =4 c: 1) среднюю скорость; 2) среднее ускорение.
=4 c: 1) среднюю скорость; 2) среднее ускорение.
Дано:
 А=6м
В=3 м/с
С=2 м/с2
D=1 м/с3
А=6м
В=3 м/с
С=2 м/с2
D=1 м/с3
 =1c =1c
 =4c =4c
| Решение:
Определим путь пройденный телом в интервале
времени 
 Тогда средняя скорость в этом интервале времени:
Тогда средняя скорость в этом интервале времени:
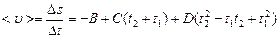
 28 м/с
Мгновенную скорость тела определим по
формуле: 28 м/с
Мгновенную скорость тела определим по
формуле:  Найдём изменение скорости тела на заданном
промежутке времени:
Найдём изменение скорости тела на заданном
промежутке времени:
 Тогда среднее ускорение на этом промежутке
времени:
Тогда среднее ускорение на этом промежутке
времени:

|

|
Пример№5: Чер.№1-25
Движение точки по прямой согласно уравнению x=At+Bt3, где А =6 м/с, В = -0,125 м/с3. Определите среднюю путевую скорость  движения точки в интервале времени от t 1=2 c до t 2=6 c.
движения точки в интервале времени от t 1=2 c до t 2=6 c.
Дано:

| Решение:
Так как  а а  , то в этом
интервале времени существует точка возврата,
в которой , то в этом
интервале времени существует точка возврата,
в которой  . Определим момент времени, в
котором . Определим момент времени, в
котором  : : 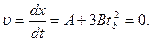 Следовательно:
Следовательно:  Для того, чтобы найти пройденный телом путь на
заданном интервале времени, нужно найти путь за
интервал от t1 до tb(s1) и сложить его с путём,
пройденным от tb до t2(s2):
Для того, чтобы найти пройденный телом путь на
заданном интервале времени, нужно найти путь за
интервал от t1 до tb(s1) и сложить его с путём,
пройденным от tb до t2(s2):  , где , где

 Тогда средняя скорость будет равна:
Тогда средняя скорость будет равна:

|

|
Пример №6. Тр.№1.10
Тело падает с высоты h= 1км с нулевой начальной скоростью. Пренебрегая сопротивлением воздуха, определить какое время понадобится телу для прохождения: 1)первых 10м своего пути; 2) последних 10 м своего пути.
Дано:
h= 1000 м

| Решение:
 Составим уравнение изменения координаты «y» тела со
временем:
Составим уравнение изменения координаты «y» тела со
временем:  1. Пройдя первые 10м пути тело будет иметь координату:
1. Пройдя первые 10м пути тело будет иметь координату:
 Поэтому: Поэтому:  и
и  2. Определим время падения тела на землю (y=0):
2. Определим время падения тела на землю (y=0):
 ; ;  Определим время, за которое тело достигает точки с
координатой y= 10:
1
Определим время, за которое тело достигает точки с
координатой y= 10:
1   Следовательно, время, за которое тело проходит последние
10 м пути равно:
Следовательно, время, за которое тело проходит последние
10 м пути равно: 
|

|
Пример №7 Тр.№1.23
|
|
|
Кинематические уравнения движения двух материальных точек имеют вид 
где В1 =4 м/с2, С1 = -3 м/с3, В2 = -2 м/с2, С2 =1 м/с3. определить момент времени, для которого ускорение этих точек будут равны.
Дано:

| Решение:
Определим уравнения мгновенных скоростей
точек: 
 Найдём зависимость мгновенных ускорений
точек от времени:
Найдём зависимость мгновенных ускорений
точек от времени:

 По условию а1=а2 отсюда
По условию а1=а2 отсюда
 Тогда искомое время равно:
Тогда искомое время равно:

|
| t -? |
Пример№8 Тр.№1.28
Точка движется в плоскости xy из положения с координатами x=y=0 со скоростью 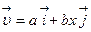 (a, b -постоянные;
(a, b -постоянные;  - орты осей x и y.)Определить: 1) уравнение траектории точки y(x); 2) форму траектории.
- орты осей x и y.)Определить: 1) уравнение траектории точки y(x); 2) форму траектории.
Дано:

| Решение:
Из уравнения для скорости: 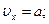  Найдём зависимость x(t):
Найдём зависимость x(t):  Тогда:
Тогда:  и и 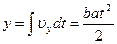 Определим уравнение траектории:
Определим уравнение траектории:  ; ;
 По виду зависимости y(x) делаем вывод, что
траектория движения тела парабола.
По виду зависимости y(x) делаем вывод, что
траектория движения тела парабола.
|
| y(x)-? |
Пример №9 Тр.№1.30
Радиус-вектор материальной точки изменяется со временем по закону  . Определить: 1) скорость
. Определить: 1) скорость 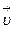 ;
;
2) ускорение  ; 3) модуль скорости в момент времени t/ =2 c.
; 3) модуль скорости в момент времени t/ =2 c.
Дано:

| Решение:
По определению: 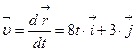
 . Так как . Так как  и и 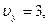 то модуль скорости в любой момент времени
равен:
то модуль скорости в любой момент времени
равен:

|

|
Пример №10 Тр.№1.31
Движение материальной точки в плоскости xy описывается законом x =At и y =At(1+Bt), где А и В- положительные постоянные. Определить: 1) уравнение траектории материальной точки y(x);
2) радиус-вектор точки  в зависимости от времени; 3) скорость
в зависимости от времени; 3) скорость 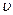 точки в зависимости от времени; 4) ускорение а точки в зависимости от времени.
точки в зависимости от времени; 4) ускорение а точки в зависимости от времени.
| Дано: x =At y =At(1+Bt) | Решение:
1.Найдём уравнение траектории:
 ; ;  2.
2.  3.Найдём составляющие скорости:
3.Найдём составляющие скорости:
 Тогда модуль скорости:
Тогда модуль скорости:
 4.Найдём составляющие ускорения:
ax=0; ay=2AB следовательно модуль
ускорения: a=ay=2AB=const
4.Найдём составляющие ускорения:
ax=0; ay=2AB следовательно модуль
ускорения: a=ay=2AB=const
|
y(x)-?

|
Заключительная часть
- Подводятся итоги занятия.
- Задаётся задание на самостоятельную работу по пройденной теме:
Т.И.Трофимова «Сборник задач по курсу физики.»
|
|
|
№1.10; 1.11; 1.19; 1.24; 1.29.
- Объявляется тема следующего занятия.
Тема 1.2: Кинематика. Криволинейное движение. Вращение тела вокруг неподвижной оси.
I. Цель практического занятия:
- Закрепить и углубить знание теоретических вопросов, основных понятий и формул кинематики.
- Учиться применять полученные знания для решения задач по данной теме.
II. Расчет учебного времени:
| Содержание занятия | Время (мин) |
Вступительная часть
Объявление темы и цели занятия.
Контрольный опрос:
|
Контрольный опрос:
- В первом способе задания криволинейного движения задается уравнение движения точки по кривой: S = f(t). Мгновенная скорость:
 .
.
Ускорение разлагается на две составляющие:  и
и 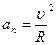 .
.
Полное ускорение: 

- При втором способе задания криволинейного движения задаются уравнения зависимости координат от времени:
 ; y = y(t)
; y = y(t)
Проекции скорости на оси координат:  ;
; 
Скорость: 
Проекции ускорения на оси координат:  ;
; 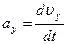
Полное ускорение:  .
.
- . При вращении вокруг неподвижной оси:
Средняя угловая скорость:  ;
;
Мгновенная угловая скорость:  ;
;
Среднее угловое ускорение: 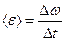 ;
;
Мгновенное угловое ускорение:  ;
;
Угол поворота и угловая скорость для равнопеременного вращательного движения: 
- Связь между линейными и угловыми величинами:
 ;
;  ;
; 
Основная часть:
Пример№1. Чер.№1-28
Точка движется по окружности радиусом R= 2м согласно уравнению  , где А=2 м/с3. В какой момент времени t нормальное ускорение
, где А=2 м/с3. В какой момент времени t нормальное ускорение  точки будет равно тангенциальному
точки будет равно тангенциальному 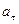 ? Определить полное ускорение а в этот момент.
? Определить полное ускорение а в этот момент.
Дано:
R=2 м
S=At3
А=2м/с3

| Решение:
Найдем мгновенную скорость: 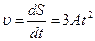 Найдем составляющие ускорения:
Найдем составляющие ускорения:
 ; ;  По условию
По условию  ; поэтому: ; поэтому:  Искомое время:
Искомое время:  Полное ускорение в этот момент времени:
Полное ускорение в этот момент времени:
 м/с2 м/с2
|
| t -? а -? |
Пример№2 Чер. №1-29
Движение точки по кривой задано уравнениями  и
и  , где
, где  ,
, 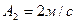 . Найти уравнение траектории точки, её скорость
. Найти уравнение траектории точки, её скорость 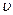 и полное ускорение а в момент времени
и полное ускорение а в момент времени 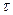 =0,8 с.
=0,8 с.
|
|
|
Дано:

| Решение:
Найдем уравнение траектории:
т.к.  , то , то  Тогда уравнение траектории: y3 – 8x = 0.
Найдем составляющие скорости:
Тогда уравнение траектории: y3 – 8x = 0.
Найдем составляющие скорости: 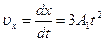 ; ;  Скорость в заданный момент времени:
Скорость в заданный момент времени:   м/с
Найдем составляющие ускорения: м/с
Найдем составляющие ускорения:  ; ; 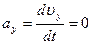 Тогда полное ускорение в заданный момент времени:
Тогда полное ускорение в заданный момент времени:  м/с2 м/с2
|
y(x) -?

|
Пример №3 Тр.№1.13
Тело брошено со скоростью 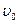 =15 м/с под углом
=15 м/с под углом 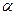 =30° к горизонту. Пренебрегая сопротивлением воздуха, определить: 1) высоту h подъёма тела; 2) дальность полёта (по горизонтали) S тела; 3) время его движения.
=30° к горизонту. Пренебрегая сопротивлением воздуха, определить: 1) высоту h подъёма тела; 2) дальность полёта (по горизонтали) S тела; 3) время его движения.
Дано:
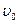 =15 м/с =15 м/с
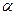 =30° =30°
| Решение:
 Составим уравнение зависимости координат от времени:
Составим уравнение зависимости координат от времени:
 Когда тело достигает максимальной высоты
Когда тело достигает максимальной высоты  , т.е. , т.е. 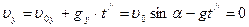 ,
тогда время подъёма тела на максимальную высоту: ,
тогда время подъёма тела на максимальную высоту:  Так как
Так как  то: то:  м
когда тело падает на Землю: м
когда тело падает на Землю:  то есть то есть  Следовательно:
Следовательно:  и и  где где  начальный момент; начальный момент;  время движения (полёта) тела.
Так как время движения (полёта) тела.
Так как 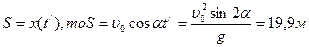
|
| h-? S-? t/-? |
Пример №4 Чер.№1-37
Камень брошен с вышки в горизонтальном направлении с начальной скоростью 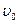 =30 м/с. Определить скорость
=30 м/с. Определить скорость 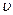 , тангенциальное
, тангенциальное 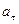 и нормальное
и нормальное  ускорения камня в конце второй секунды после начала движения.
ускорения камня в конце второй секунды после начала движения.
Дано:
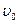 =30м/с =30м/с
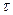 =2с =2с
| Решение:
 Найдём составляющие скорости:
Найдём составляющие скорости:
 ; ;  тогда скорость в заданный момент времени:
тогда скорость в заданный момент времени:  =36 м/с
Так как полное ускорение – это =36 м/с
Так как полное ускорение – это  , то из рисунка: , то из рисунка:
 Так как
Так как  то радиус кривизны траектории в этот момент времени: то радиус кривизны траектории в этот момент времени:  =158м. =158м.
|

|
Пример №5 Тр.№1.32
Материальная точка начинает двигаться по окружности радиусом r= 12,5 см с постоянным тангенциальным ускорением 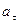 =0,5 с
=0,5 с  . Определить: 1) момент времени при котором вектор ускорения
. Определить: 1) момент времени при котором вектор ускорения  образует с вектором скорости
образует с вектором скорости 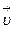 угол
угол 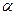 =45°; 2) путь, пройденный за это время движущейся точкой.
=45°; 2) путь, пройденный за это время движущейся точкой.
Дано:
r=0,125м
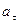 =0,005 =0,005 
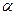 =45° =45°
| Решение:
 Так как
Так как 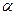 =45°, то =45°, то  .
Так как в задаче равноускоренное движение по окружности, то: .
Так как в задаче равноускоренное движение по окружности, то:  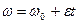 и и  Считая, что
Считая, что  , получим: , получим:  В момент времени
В момент времени 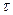 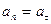 , поэтому: , поэтому:  и и 

|

|
Пример №6 Тр.(стр.7) задача№2
Диск радиусом R=5см вращается вокруг неподвижной оси так, что зависимость угловой скорости от времени задаётся уравнением  . Определить для точек на ободе диска к концу первой секунды после начала движения:
. Определить для точек на ободе диска к концу первой секунды после начала движения:
1) полное ускорение; 2) число оборотов, сделанных диском.
Дано:
R=0,05м

| Решение:
Найдём угловое ускорение:  Нормальное и тангенциальное ускорения:
Нормальное и тангенциальное ускорения:
 Тогда полное ускорение:
Тогда полное ускорение:
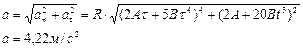 Так как угол поворота диска
Так как угол поворота диска  , то , то  Угловая скорость
Угловая скорость  , поэтому , поэтому  Тогда число оборотов, сделанных диском за
время
Тогда число оборотов, сделанных диском за
время 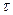 : : 
|
| a-? N -? |
Пример№7 Тр.№1.39
Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задаётся уравнением 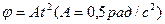 . Определить к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное
. Определить к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное 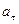 , нормальное
, нормальное  и полное а ускорения.
и полное а ускорения.
Дано:

| Решение:

|

|
Пример№8 Чер.№1-42
На цилиндр, который может вращаться около горизонтальной оси, намотана нить. К концу нити привязали грузик и предоставили ему возможность опускаться. Двигаясь равноускоренно, грузик за время t= 3 c опустился на h =1,5 м. Определить угловое ускорение 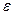 цилиндра, если его радиус r =4 см.
цилиндра, если его радиус r =4 см.
| Дано: t=3c h=1,5м r=0,04м | Решение:
 Грузик опускается с ускорением. Так как
Грузик опускается с ускорением. Так как  , то , то  и и  Это ускорение является тангенциальным так как нить не проскальзывает. Тогда угловое ускорение:
Это ускорение является тангенциальным так как нить не проскальзывает. Тогда угловое ускорение: 
|
|
Заключительная часть:
Задание на самостоятельную работу:
Т.И.Трофимова «Сборник задач по курсу физики» №1.14; 1.34; 1.36; 1.40
|
|
|





