 |
30. Методы построения сокращенных ДНФ. Минимизация ДНФ. Геометрическая интерпретация. Метод Блейка.
|
|
|
|
30. Методы построения сокращенных ДНФ. Минимизация ДНФ. Геометрическая интерпретация. Метод Блейка.
a) При небольших значениях n можно использовать геометрическое изображение множества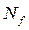 
в кубе 
. Для искомого построения в кубе 
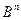отыскиваются грани максимальной размерности, содержащиеся в множестве 
, а затем составляется ДНФ из конъюнкций, соответствующих этим граням.
b) Метод Блейка заключается в применении слева направо правил обобщенного склеивания 
и поглощения 
, причем на первом этапе применяется правило обобщенного склеивания до тех пор, пока это возможно, а на втором – правило поглощения;
c) Алгоритм Квайна применяется к формуле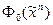 
, заданной в виде совершенной ДНФ. На первом этапе находится ДНФ 
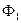, для чего сначала к каждой паре конъюнкций формулы 
(если это возможно) применяется операция неполного склеивания: 
, а затем для удаления возможных конъюнкций ранга n используется операция поглощения: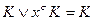 
. На 
-м этапе операции неполного склеивания и поглощения применяются к конъюнкциям ранга 
ДНФ 
, полученной на k-м этапе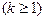 
. В результате находится ДНФ 
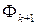, и алгоритм заканчивает работу, если 
.
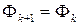Наиболее простой (ручной) способ построения сокращенной ДНФ для функций небольшого числа переменных состоит в использовании минимизирующих карт, называемых картами Карно или диаграммами Вейч а. Он основан на задании функции прямоугольной таблицей, причем наборы значений переменных на каждой из сторон прямоугольника записываются в коде Грея.
Нахождение простых импликант сводится к выделению в таблице максимальных по включению прямоугольников, состоящих из единиц. Дополнительно полагается, что каждая клетка таблицы, примыкающая к одной из сторон прямоугольника, является соседней к клетке, примыкающей к противоположной стороне и расположенной на той же горизонтали или вертикали.
|
|
|
31. Метод минимизирующих карт (карт Карно). Реализация булевых функций схемами из функциональных элементов.
Наиболее простой (ручной) способ построения сокращенной ДНФ для функций небольшого числа переменных состоит в использовании минимизирующих карт, называемых картами Карно или диаграммами Вейча. Он основан на задании функции прямоугольной таблицей, причем наборы значений переменных на каждой из сторон прямоугольника записываются в коде Грея.
Нахождение простых импликант сводится к выделению в таблице максимальных по включению прямоугольников, состоящих из единиц. Дополнительно полагается, что каждая клетка таблицы, примыкающая к одной из сторон прямоугольника, является соседней к клетке, примыкающей к противоположной стороне и расположенной на той же горизонтали или вертикали.
Метод Карно основан на законе склеивания. Склеиваются наборы, отличающиеся друг от друга лишь значением одного разряда. Такие наборы называются соседними, и они соответствуют соседним клеткам карты Карно. Формируются такие наборы(коды Грея) по принципу симметрии.
Введем определение прямоугольника Карно, под которым будем понимать некоторую, зачастую разрозненную, фигуру покрытия, удовлетворяющую принципу симметрии, т. е. сплошь состоящую из элементарных прямоугольников Карно, закодированных только соседними наборами.
Этот метод применим также и для не всюду определенных функций. В этом случае выделяются максимальные прямоугольники, содержащие хотя бы одну единицу и не содержащие нулей.
Например, функции 
соответствует минимизирующая карта, представленная таблицей 1.
Таблица 1. Карта Карно функции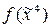 
.
 
| ||||
| 0 0 | 11 | 1 | ||
| 0 1 | 11 | |||
| 1 1 | 11 | |||
| 1 0 | 1 |
В таблице 1 для упрощения выделения требуемых прямоугольников пропущены нулевые значения функции, а единичные значения, объединяемые в соответствующие прямоугольники, обозначены 1 и 1. Коды максимальных интервалов представимы в следующей форме:
|
|
|
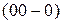– соответствует прямоугольнику из строки 1 и столбцов 1, 4;
– соответствует прямоугольнику из строки 1 и столбцов 1, 2;
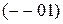– соответствует прямоугольнику из строк 1, 2, 3, 4 и столбца 2;
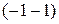– соответствует прямоугольнику из строк 2, 3 и столбцов 2, 3;
– соответствует прямоугольнику из строки 3 и столбцов 1, 2.
Поэтому сокращенная ДНФ функции принимает следующий вид:
.
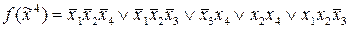При нахождении тупиковых ДНФ можно использовать алгоритм Квайна, дополняемый исследованием специальной таблицы, и карты Карно.
При построении кратчайших ДНФ на карте Карно отыскивается минимальная по числу элементов совокупность прямоугольников, отвечающих простым импликантам функции и покрывающих все единицы карты Карно. В частности, в рассмотренном примере найдена кратчайшая ДНФ функции .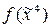
|
|
|
