 |
32. Полнота и замкнутость. 33.Важнейшие замкнутые классы. Теорема о полноте. Примеры функционально полных базисов.
|
|
|
|
32. Полнота и замкнутость
Всякая функция алгебры логики (булева алгебра) может быть выражена в виде формулы через элементарные функции(Ù, Ú и отрицание), а также представлена в табличном виде. Рассмотрим некоторые свойства элементарные функций.
Таблица элементарных функций на P2, т. е. {0, 1}.
| х | Название функции | Обозначение | ||||
| у | ||||||
| f0(x, y) | Константа “0” | |||||
| f1(x, y) | Конъюнкция | x Ù y , xy, x& y | ||||
| f2(x, y) | Операция запрета по y | 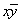
| ||||
| f3(x, y) | Переменная x | x | ||||
| f4(x, y) | Операция запрета по x | 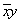
| ||||
| f5(x, y) | Переменная y | y | ||||
| f6(x, y) | Сумма по модулю 2 | x Å y | ||||
| f7(x, y) | Дизъюнкция | x Ú y | ||||
| f8(x, y) | Операция Пирса | x¯ y | ||||
| f9(x, y) | Равнозначность | x~y | ||||
| f10(x, y) | Инверсия y | 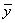
| ||||
| f11(x, y) | Импликация от y к x | y®x | ||||
| f12(x, y) | Инверсия x | 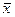
| ||||
| f13(x, y) | Импликация от x к y | x®y | ||||
| f14(x, y) | Операция Шеффера | x / y | ||||
| f15(x, y) | Константа “1” |
Определение1. Система функций {f1, f2,... }из Р2 называется (функционально) полной, если любая булева функция может быть записана в виде формулы
через функции этой системы.
Рассмотрим примеры полных систем.
1. Система Р2 - множество всех булевых функций — является полной системой.
2. Система y = { 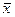 , x1& x2, x1Ú х2} представляет полную систему.
, x1& x2, x1Ú х2} представляет полную систему.
Не каждая система является полной, например, система y = {0, 1) не полная.
Теорема 1. Пусть даны две системы функций из Р2 y={f1, f2,... } и G={g1, g2,... } относительно которых известно, что система y полна и каждая ее функция выражается в виде формулы через функции системы G. Тогда система G явл. полной.
|
|
|
На основе теоремы 1 приведем примеры еще полных систем:
y={ 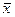 , x1& x2}, y={
, x1& x2}, y={ 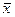 , x1 Ú х2}, y={ x / y}, y={0, 1, х1х2, х1Å х2} (доказывается из осн. свойств булевой алгебры)
, x1 Ú х2}, y={ x / y}, y={0, 1, х1х2, х1Å х2} (доказывается из осн. свойств булевой алгебры)
Теорема 2. Каждая функция из P2 может быть выражена при помощи полинома по mod 2(полинома Жегалкина).
Таким образом, видно что существует ряд полных систем. Каждая из них может быть принята за множество элементарных функций.
Определение 2. Пусть y - некоторое подмножество функций из P2. Замыканием называется множество всех булевых функций, представимых в виде формул через функции множества y. Замыкание множества y обозначается через [y]. Замыкание инвариантно относительно операций введения и удаления фиктивных переменных.
Примеры: 1)y=P2, следовательно [y] = P2 (замыканием явл. сама сист. );
2) y={1, x1+x2}. Замыканием будет класс L линейных функций, т. е. фун-й, имеющих вид f=(x1, …xn)=c0+c1x1+…+cnxn, где с1=0(фиктивные переменные)или 1(существенные).
Свойства замыкания:
1) y  [y]
[y]
2) [[y]]=[y]
3) если y1  y2, то [y1]
y2, то [y1]  [y2]
[y2]
4) [y1 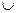 y2]
y2] 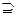 [y1]
[y1] 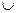 [y2]
[y2]
Определение 3. Класс (множество) y называется (функционально) замкнутым, если [y]=y.
Примеры: класс y=P2 явл замкнутым; 2) класс y={1, x1+x2} не замкнут.
Следствие: Система будет полной, если ее замыкание совпадает с P2 , [y] = P2
33. Важнейшие замкнутые классы. Теорема о полноте. Примеры функционально полных базисов.
1)Обозначим через T0 класс всех булевых функция f=(x1, …xn), сохраняющих константу 0, т. е. функций, для которых выполнено равенство f=(0, …0)=0.
функции 0; x; x1& x2; x1Vх2; х1Å х2- принадлежат T0, а 1,  - нет.
- нет.
2) Обозначим через T1 класс всех булевых функций f =(x1, …xn), сохраняющих константу 1, т. е. функций для которых выполнено равенство f=(1, …1)=1.
функции 0; x; x1& x2; x1Vх2; х1Å х2- принадлежат T1, а 1,  - нет.
- нет.
3)Обозначим через S класс всех самодвойственных функций, т. е. функций f из P2 таких, что  . т. е.
. т. е. 
самодвойственные функции x и  .
.
4) Класс М функций f=(x1, …xn) называется монотонным, если для любых двух наборов 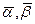 , таких что
, таких что  имеет место неравенство
имеет место неравенство 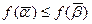
|
|
|
монотонные функции: 0; 1; x; x1& x2; x1Vх2
5) Класс L функций f=(x1, …xn) называется линейной, если fm(x1, ..., xn) = a0Å a1x1Å ... Å anxn, где ai  {0; 1}. К классу L принадлежат функции 0, 1,
{0; 1}. К классу L принадлежат функции 0, 1, 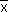 , x~y, xÅ y.
, x~y, xÅ y.
Теорема1 (о функциональной полноте): Для того чтобы система функций y была полной, необходимо и достаточно, чтобы она не содержалась ни в одном из пяти замкнутых классов T0, T1, S, M и L
Следствие1: Всякий замкнутый класс y функций из P2 , такой, что y P2 , содержится по крайней мере в одном из построенных классов. 
Определение 2. Класс y функций из P2 , называется предполным (максимальным), если y неполный, а для любой функции f (f  P2 , f
P2 , f 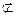 y) класс y
y) класс y 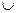 {f} - полный. Из определения следует что предполный класс явл. замкнутым.
{f} - полный. Из определения следует что предполный класс явл. замкнутым.
Следствие 2: В алгебре логики существует только пять предполных классов T0, T1, S, M и L.
Теорема3: Из всякой полной в P2 системы y функций можно выделить полную подсистему, содержащую не более четырех функций.
Следствие 3: Теорема о функциональной полноте позволяет найти для произвольной булевой функции f формулу через функцию полной системы y.
Теорема4(Поста): Функциональный базис B является полным тогда и только тогда, когда он целиком не содержится ни в одном из пяти замкнутых классов T0, T1, S, M, L. Иначе говоря, функциональный базис B является полным тогда и только тогда, когда он содержит: хотя бы одну функцию, не принадлежащую классу T0 (T1, S, M, L).
Примеры функционально полных базисов, используя таблицу двух переменных.
1)Базис 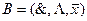 . Любая функция, не равная тождественно нулю, может быть представлена формулой в СДНФ (следствие из теоремы Шеннона). Константы 0, 1 могут быть представлены в виде:
. Любая функция, не равная тождественно нулю, может быть представлена формулой в СДНФ (следствие из теоремы Шеннона). Константы 0, 1 могут быть представлены в виде:  . Из базиса можно получить еще два функционально полных базиса:
. Из базиса можно получить еще два функционально полных базиса:
{Ù , 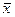 }, так как
}, так как 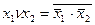 ; {v,
; {v, 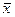 }, так как
}, так как 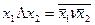
Базис функционально полон, поскольку для любой функции может быть построен полином Жегалкина над этим базисом.
2)Поскольку константу 0 можно получить как 0 = 1 Å 1, функционально полным будет также базис {Ù, Å, 1}. Доказательством этого служит то, что константа 1 не принадлежит классу Т0, тогда как обе функции Ù и Å принадлежат этому классу, что обеспечивает справедливость теоремы о функциональной полноте.
|
|
|
Однако базис {Ù , Å, 0} уже не будет функционально полным, так как невозможно выразить константу 1 формулой над этим базисом, ибо константа 0 принадлежит классу Т0, как и функции Ù и Å.
3)Важными примерами функционально полных базисов являются универсальные базисы {/}, {↓ }, содержащие по одной переключательной функции.
|
|
|


