35. Схемы алгоритмов, схемы потоков данных и использовании теории графов и теории конечных автоматов для их описания.

Задачи теории графов:

• задача о кенигсбергских мостах (задача Эйлера), развитие которой привело к циклу задач об обходах графов;
• задачиоперевозках, решение которых привело к созданию эффективных методов решения транспортныхзадач;
• задачаочетырехкрасках;
• Нахождение кратчайшего пути – одна из часто встречаемых прикладных задач, которую можно интерпретировать на языке теории графов как нахождение кратчайшего пути между двумя вершинами. К этим задачам, в частности, относится широко известная задача о волке, козе и капусте.
• Понятия, введенные при определении связности графа G, также используются при решении ряда прикладных задач. Например, для множества членов  некоторой организации ребро  означает, что лица  могут общаться между собой. Точками сочленения графа 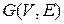 являются связные, представляющие особо уязвимое звено, так как их утрата приводит к нарушению единства и сплоченности этой организации.
• Схема алгоритмов в программировании
• Кирхгоф при составлении полной системы уравнений для токов и напряжений в электрической схеме предложил, по существу, представлять такую схему графом и находить в нем деревья, с помощью которых выделяются линейно независимые системы контуров.
• Кэли, исходя из задач подсчета числа изомеров предельных углеводородов, пришел к задачам перечисления и подсчета деревьев, обладающих заданными свойствами.
• К комбинаторным направлениям задач в теории графов относятся, например, задачи о построении графов с заданными свойствами, задачи о подсчете и перечислении графов с фиксированными свойствами.
• Примером результатов геометрического направления является выделение маршрутов, содержащих все вершины или все ребра графа. Известен критерий существования обхода всех ребер графа: в связном графе цикл, содержащий все ребра и проходящий по каждому ребру только один раз, существует тогда и только тогда, когда все вершины графа имеют четные степени.
• Прианализе надежности сетей связи, электронных схем, коммуникационных сетей возникает задача о нахождении количеств непересекающихся цепей, соединяющих различные вершины графа. Так, например, наименьшее число вершин, разделяющих две несмежные вершины графа, равно наибольшему числу непересекающихся по вершинам простых цепей, соединяющих эту пару вершин.
• раскраски графов - разбиения множества вершин (ребер), обладающие определенными свойствами, например, смежные вершины (ребра) должны принадлежать различным множествам (вершины и ребра из одного множества окрашиваются одним цветом). Так, что наименьшее число цветов, достаточное для раскраски ребер любого графа без петель с максимальной степенью вершин s, равно [ 3 s/ 2 ], а для раскраски вершин любого графа без петель и кратных ребер достаточно s + 1 цветов.
•  Для решения задач, связанных с печатным монтажем электронных схем, модельной является задача оразбиении данного графа на минимальное число плоских графов.
• Путь проходящие в точности один раз через каждую вершину (а не каждое ребро) данного графа называется гамильтоновым путем. Проблема существования гамильтонова пути принадлежит к классу так называемых NP-полных задач, т. е. для решения не известен полиномиальный алгоритм (т. е. с числом шагов, ограниченным полиномом от размерности задачи). Очевидный алгоритм, это полный перебор всех возможностей: генерируем все n! различных последовательностей вершин и для каждой из них проверяем, определяет ли она гамильтонов путь. Такие действия требуют по меньшей мере n! n шагов
• Химические графыдают возможность прогнозировать хим. превращения, пояснять сущность и систематизировать нек-рые осн. понятия химии: структуру, конфигурацию, конформации, квантовомех. и статистико-мех. взаимодействия молекул, изомерию и др. К хим. графам относятся молекулярные, двудольные и сигнальные графы кинетич. ур-ний р-ций.
• Молекулярные графы, применяемые в стереохимии и структурной топологии, химии кластеров, полимеров и др., представляют собой неориентированные графы, отображающие строение молекул. Вершины и ребра этих графов отвечают соотв. атомам и хим. связям между ними.

Теорию потоков лучше всего представлять как совокупность моделей и методов решения разнообразных транспортных задач. Задача о максимальном потоке и ее эффективное алгоритмическое решение образует фундамент нового раздела математики – комбинаторной оптимизации.

Пусть в орграфе G выделены две вершины: s – источник и t – сток, а также определена функция: 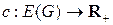, которая сопоставляет каждой дуге  неотрицательное действительное число , называемое пропускной способностью этой дуги. В неориентированном графе каждое ребро можно заменить двумя дугами, имеющими противоположную ориентацию.

Четверка  называется сетью, а функция 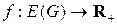 называется потоком в сети G, если она удовлетворяет следующим условиям:

a) 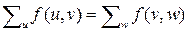для всех вершин 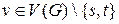– свойство сохранения потока;

b) для всех .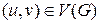

Разность  называется величиной 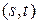 потока. Можно показать, что в каждой сети G существует максимальный поток, т. е. поток с максимально возможной величиной.