 |
43.Метод касательных. 44.Метод наискорейшего спуска.. 45.Метод покоординатного спуска.
|
|
|
|
43. Метод касательных.
Определение минимума функции методом касательных.
Определение. Множество X n-мерного евклидового пространства En называется выпуклым, если вместе с любыми двумя точками  и
и  ему принадлежит и соединяющий их отрезок
ему принадлежит и соединяющий их отрезок  .
.
Выпуклость множества X означает, что из 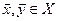 следует
следует 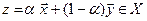 для всех
для всех  .
.
Определение. Скалярная функция  называется выпуклой на выпуклом множестве X, если для любых
называется выпуклой на выпуклом множестве X, если для любых  и
и  выполняется неравенство
выполняется неравенство
 (1)
(1)
Если же
 (2)
(2)
то функция  называется вогнутой. Если для
называется вогнутой. Если для 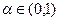 неравенство (1) – строгое, то
неравенство (1) – строгое, то  называют строго выпуклой (соответственно для (2) – строго вогнутой). Сумма выпуклых (вогнутых) функций является выпуклой (вогнутой) функцией.
называют строго выпуклой (соответственно для (2) – строго вогнутой). Сумма выпуклых (вогнутых) функций является выпуклой (вогнутой) функцией.
Пусть в интервале [a; b] задана выпуклая функция  . Требуется с заданной точностью
. Требуется с заданной точностью  методом касательных найти точку минимума этой функции (x*) и значение функции в этой точке (
методом касательных найти точку минимума этой функции (x*) и значение функции в этой точке (  ).
).
Алгоритм решения задачи:
1-й шаг (нестандартный). Полагаем 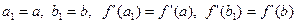 .
.
k-й шаг (  ). Если
). Если  , то точность достигнута. Возьмем
, то точность достигнута. Возьмем  и найдем
и найдем  . Если
. Если  , то определяем абсциссу xk точки пересечения прямых
, то определяем абсциссу xk точки пересечения прямых

и
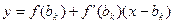 .
.
Затем вычисляем  . Если
. Если  , то минимум найден: x*=xk. Процесс заканчивается. Если
, то минимум найден: x*=xk. Процесс заканчивается. Если  , то полагаем ak+1 = xk, bk+1 = bk. Если
, то полагаем ak+1 = xk, bk+1 = bk. Если 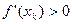 , то полагаем
, то полагаем 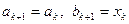 , и k-й шаг закончен.
, и k-й шаг закончен.
44. Метод наискорейшего спуска.
Метод применяется для нахождения минимума некоторой функции  = f(x1, x2, ..., xn), заданной в евклидовом пространстве, где
= f(x1, x2, ..., xn), заданной в евклидовом пространстве, где 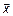 = (x1, x2, ..., xn) — вектор. Численные методы отыскания экстремума функции состоят в построении последовательности векторов {
= (x1, x2, ..., xn) — вектор. Численные методы отыскания экстремума функции состоят в построении последовательности векторов {  }, удовлетворяющих условию: f(
}, удовлетворяющих условию: f( 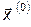 ) > f(
) > f( 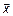 (1)) > ... > f(
(1)) > ... > f( 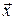 (n)). Методы построения таких последовательностей называются методами спуска. В этих методах элементы последовательности {
(n)). Методы построения таких последовательностей называются методами спуска. В этих методах элементы последовательности { 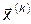 } вычисляются по формуле
} вычисляются по формуле
|
|
|
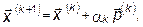 (k = 0, 1, 2,... …),
(k = 0, 1, 2,... …),
где вектор  (k) определяет направление спуска;
(k) определяет направление спуска;  — длина шага в данном направлении.
— длина шага в данном направлении.
Градиент функции в точке  направлен в сторону наискорейшего локального возрастания функции. Следовательно, направление спуска должно быть противоположным градиенту. Вектор, противоположный градиенту, называется антиградиентом. Выбирая антиградиент в качестве направления спуска, приходят к итерационному процессу вида
направлен в сторону наискорейшего локального возрастания функции. Следовательно, направление спуска должно быть противоположным градиенту. Вектор, противоположный градиенту, называется антиградиентом. Выбирая антиградиент в качестве направления спуска, приходят к итерационному процессу вида
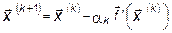 (k = 0, 1, 2,... ),
(k = 0, 1, 2,... ),
где  в точке
в точке 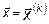 .
.
Все методы спуска, в которых вектор 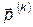 совпадает с антиградиентом, называются градиентными методами. Они отличаются друг от друга только выбором шага. Наибольшее применение нашли метод наискорейшего спуска и метод дробления шага. В методе наискорейшего спуска величина
совпадает с антиградиентом, называются градиентными методами. Они отличаются друг от друга только выбором шага. Наибольшее применение нашли метод наискорейшего спуска и метод дробления шага. В методе наискорейшего спуска величина  определяется из условия
определяется из условия
 ,
,
т. е. на каждом шаге решается одномерная задача минимизации. Для решения этой задачи можно применить метод золотого сечения. Отметим, что на двух последовательных шагах решения направления спуска ортогональны. Для окончания процесса счета можно использовать различные критерии. Например, счет можно прекратить, если выполняется условие
|| grad f( 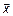 (k+1)) || < e, где || grad f || =
(k+1)) || < e, где || grad f || = 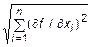 . В этом случае полагаем
. В этом случае полагаем 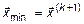 .
.
45. Метод покоординатного спуска.
Метод применяется для отыскания минимума функции n перемен- ных. Выбирается некоторое начальное приближение х(0) точки минимума функции. Затем выбирается направление спуска параллельно оси 0х1 и решается задача одномерной минимизации функции. Величина a0 определяется из условия

.
Затем определяется первое приближение точки минимума  а все остальные координаты остаются без измене- ния. При следующем уточнении точки минимума спуск производится вдоль линии, параллельной оси 0х2. Величина a1 определяется из условия
а все остальные координаты остаются без измене- ния. При следующем уточнении точки минимума спуск производится вдоль линии, параллельной оси 0х2. Величина a1 определяется из условия
|
|
|
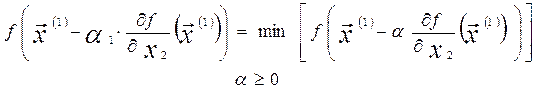 .
.
Затем определяется второе приближение точки минимума  а все остальные координаты остаются без изменения. Аналогичным способом спуск продолжается в направлении следующих координат. После этого спуск снова начинается в направлении пер- вой, второй и т. д. координаты. Процесс заканчивается при выполнении условия
а все остальные координаты остаются без изменения. Аналогичным способом спуск продолжается в направлении следующих координат. После этого спуск снова начинается в направлении пер- вой, второй и т. д. координаты. Процесс заканчивается при выполнении условия
||grad f( 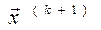 )|| < e.
)|| < e.
Пример. Найти минимум функции
f (x1, x2) = 2x1 - 3x2 + exp (x12 + x24).
Задачу решим методом покоординатного спуска. Возьмем e = 0, 001. В качестве начального выберем вектор  = (0; 0). Тогда
= (0; 0). Тогда




grad f = 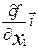 +
+ 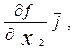 grad
grad 
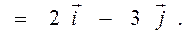
|| grad  || » 3, 60555.
|| » 3, 60555.
Составим функцию  которую нужно минимизировать по параметру a. Для минимизации этой функции применим метод дробления шага.
которую нужно минимизировать по параметру a. Для минимизации этой функции применим метод дробления шага.
|
|
|


