 |
41.Нормальное распределение.. 42. Метод золотого сечения
|
|
|
|
41. Нормальное распределение.
Нормальное распределение непрерывной случайной величины X имеет место, если r(плотность) распределения имеет вид:
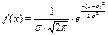, где a = M(x) (мат. ожидание), s = s(x) (ср. кв. отклонение)
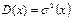
Нормальный закон распределения также называется законом Гаусса.
Можно заметить, что функция распределения F(x) является некоторой функцией 
. Эта функция 
имеет значения взаимосвязанные со значениями Лапласа.
Т. о. функция распределения для нормального распределения может быть вычислена с помощью формулы Лапласа.
Свойства:
1. Функция Лапласа является нечетной Ф(-x) = -Ф(x).
Значения функции Лапласа на 
: 
Частным случаем нормального распределения, имеющие большие приложения, являются стандартные распределения.
a=0, s=1.
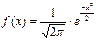
Вероятность попадания нормального распределения случайной величины x в заданный интервал [a; b] определяется формулой:
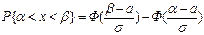
Плотность вероятности (Зелёная линия соответствует стандартному нормальному распределению)
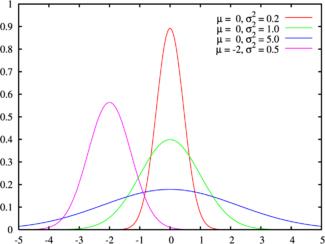
Функция распределения
42. Метод золотого сечения
Метод предназначен для определения минимума унимодальной функции одного переменного. Функция f(x) называется унимодальной в интервале [a, b], если в этом интервале существует единственная точка х*, в которой она принимает экстремальное значение. В дальнейшем будем считать, что х* — точка минимума.
Строится последовательность вложенных интервалов [a, b], [a1, b1], [a2, b2],..., [an, bn],... таким образом, чтобы х*Î [an, bn] при любом n и (bn - an)®0 при n ® ¥. Алгоритм построения этих интервалов cледующий. В интервале [a, b] выбираются две различные точки a < x1 < x2 < b и находятся значения f(x) в этих точках. Если f (x1) < f (x2), то за интервал [a1, b1] принимается [a, x2], а в противном случае [x1, b]. Затем процесс построения интервалов повторяется.
|
|
|
Золотым сечением отрезка называется такое деление отрезка на два, при котором отношение длины всего отрезка к длине большей части равно отношению длины большей части к длине меньшей части. Таких точек в отрезке две. Если в качестве точек x1 и x2 взять точки золотого сечения отрезка, то метод приближенного определения минимума функции будет называться методом золотого сечения.
Обозначим длину интервала [a, b] через l. Тогда будем считать, что tl — длина большей части отрезка при делении его по методу золотого сечения. Тогда для определения t можно составить пропорцию: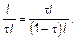 
Из этого соотношения следует, что t2 + t —
— 1 = 0. Решая квадратное уравнение и учитывая, что t > 0, найдем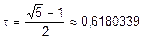 
.
Легко проверить, что если точки х1 и х2 являются точками золотого сечения отрезка [a, b], то точка х1 является одной из точек золотого сечения отрезка [a, x2], а точка х2 — отрезка [x1, b]. Таким образом при втором и следующих шагах алгоритма значение функции нужно будет вычислять только один раз.
Из приведенного алгоритма видно, что b1 - a1 = t(b - a),..., bn - an = tn(b - a). После выполнения n итераций за приближенное значение принимается величина xприбл. = (an + bn)/2. Если значение х* нужно найти с точностью e, то условием прекращения итераций является следующее неравенство:
bn - an £ 2e.
При использовании данного метода сначала нужно определить интервал [a, b], в котором находится минимум функции. Это производится путем построения графика функции y = f(x). Если интервал [a, b] будет определен неверно, то программа в качестве приближенного значения минимума выдаст величину, находящуюся вблизи одной из границ интервала [a, b]. В этом случае нужно изменить значения a и b и снова решать задачу.
|
|
|
