 |
36.Формула полной вероятности.
|
|
|
|
36. Формула полной вероятности.
Пусть А может наступить при условии появления одного из не совместных событий В1, В2, …, Вn, которые образуют полную группу. В1, В2, …, Вn – гипотезы, т. к. заранее не известно какое из них произойдёт совместно с А.
Тогда вероятность появления А.
Р(А)=Р(В1)*РВ1(А)+Р(В2)*РВ2(А) – формула полной вероятности
(События А1, А2, …, Аn попарно не совмест, если любые два из них несовм.
А1, А2, …, Аn –образуют полную группу, если они попарно не совместимы и проходит только 1)
37. Формула Бейеса.
Условная вероятность гипотезы Вi в предположении, что событие А уже имеет место, определяется по формуле Бейеса
 .
.
Словами:
Пусть имеется полная группа несовместных гипотез Вi с известными вероятностями их наступления P(Вi). Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны. Требуется определить какие вероятности имеют гипотезы относительно события А, т. е. условные вероятности Вi.
Теорема Бейеса: Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.
(Теорема умножения вероятностей.
Вероятность совместного появления двух событий = произведению вероятности одного из них на условную вероятность другого, вычислить предположения, что 1 событие уже наступило.
Р(АВ)=Р(А)*РА(В))
38. Формула Бернулли.
Схема испытания должна быть удовлетворена следующим условиям:
Число испытаний конечно – n
В результате каждого испытания может быть 2-а исхода: 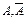
Если вероятность события 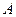 в отдельном взятом испытании
в отдельном взятом испытании  то
то 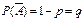
|
|
|
Вероятность 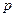 и
и 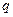 не меняется от испытания к испытанию. Вероятность того, что событие
не меняется от испытания к испытанию. Вероятность того, что событие 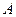 наступит ровно m раз в n- испытаниях, удовлетворяет схеме испытания Бернулли, вычисляемое по формуле Бернулли:
наступит ровно m раз в n- испытаниях, удовлетворяет схеме испытания Бернулли, вычисляемое по формуле Бернулли: 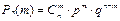 , m=0, 1, 2, .. , n
, m=0, 1, 2, .. , n
Следствие:
Вероятность того, что в n-испытаниях удовлетворяет схеме испытания Бернулли, событие 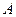 натупит:
натупит:
Менее m-раз: 
Более m-раз: 
Хотя бы 1 раз: 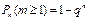
Вероятность того, что событие 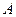 наступит в в n-испытаниях, такое число раз, которое заключено в приделах от m1 до m2:
наступит в в n-испытаниях, такое число раз, которое заключено в приделах от m1 до m2:  Обозначим m0- наивероятнейшее число наступления события
Обозначим m0- наивероятнейшее число наступления события 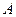 в n-испытаниях:
в n-испытаниях: 
Полиноминальное распределение
Пусть проводится n-испытаний. В результате каждого испытания могут произойти события 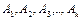 с вероятностью:
с вероятностью:  ,
, 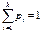 . Вероятность того, что в n-испытаний, событие
. Вероятность того, что в n-испытаний, событие  появится m1 раз,
появится m1 раз, 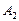 появится m2 и т. д.
появится m2 и т. д.
(m1+ m2+ …. + mk = n). Задается формулой полиноминального распределения: 
Замечание: Схема Испытания Бернулли является частным случаем полиноминального распределения, если k=2
39. Функция распределения, плотность распределения и их свойства. Связь между ними.
Закон распределения НСВ (непрерывной случайной величины) можно задать с помощью функций:
Функция распределения F(x)
Функция плотности распределения вероятностей f(x)
Кумулятивная функция распределения (или просто функция распределения) в теории вероятностей однозначно задаёт распределение случайной величины или случайного вектора.
Функция распределения любой случайной величины обладает следующими свойствами:
· F(x) определена на всей числовой прямой R;
· F(x) не убывает, т. е. если x1< =x2, то F(x1)< =F(x2);
· F(-∞ )=0, F(+∞ )=1, т. е. 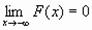 и
и  ;
;
·  F(x) непрерывна справа, т. е.
F(x) непрерывна справа, т. е.
Плотность вероятности — один из способов задания вероятностной меры на евклидовом пространстве Rn. (Вероятность (вероятностная мера) — мера достоверности случайного события. Оценкой вероятности события может служить частота его наступления в длительной серии независимых повторений случайного эксперимента. )
|
|
|
Функцией плотности распределения вероятностей НСВ называется производная ее функции распределения.
Свойства f(x)
f(x) 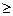 0
0

p(a  X
X  b)=
b)= 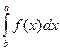
f(  )=0
)=0
F(x)= 
График функции плотности распределения вероятности f(x) называется кривой распределения.
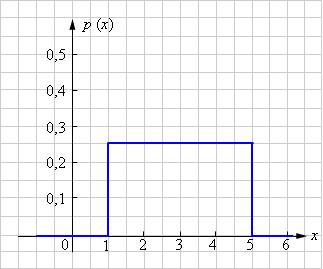 Плотность вероятности постоянного распределения
Плотность вероятности постоянного распределения
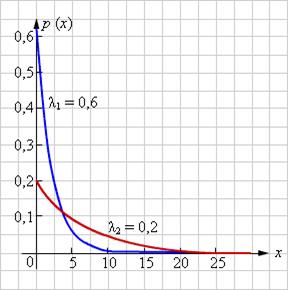
 Плотность вероятности экспоненциального распределения
Плотность вероятности экспоненциального распределения
 Плотность вероятности нормального распределения
Плотность вероятности нормального распределения
На основе ряда распределения можно получить функцию распределения дискретной случайной величины X. Эта функция выражается следующей формулой:
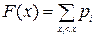
Формулу можно записать в следующем виде, наглядно иллюстрирующем непрерывность слева функции распределения:
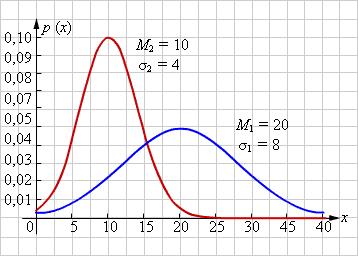
График функции распределения дискретной случайной величины обычно представляет собой ступенчатую линию (рис. 2. 1).
Функция распределения непрерывной случайной величины X представляется в виде интеграла
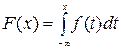 (*)
(*)
График функции распределения 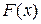 непрерывной случайной величины представляет собой непрерывную кривую (рис. 2. 2).
непрерывной случайной величины представляет собой непрерывную кривую (рис. 2. 2).

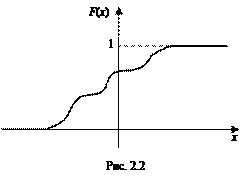
40. Числовые характеристики случайных величин.
Закон распределения плотностью описывает СВ. При решении некоторых задач не нужно знать полное описание СВ. Достаточно знать только отдельные ее числовые характеристики.
Важнейшие характеристики СВ
- Математическое ожидание СВ (МО)
- Дисперсия СВ
- Среднее квадратическое отклонение СВ
МО (среднее значение) ДСВ называется сумма произведений всех ее возможных значений на соответствующие вероятности.
M(X)= 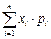
МО НСВ Х с плотностью распределения вероятностей f(x) называется число находимое по формуле. M(Х)= 
1. М(С)=С, С=const
2. М(С*x)=C*М(С)
3. М(x_+y)= М(x)_+ М(y)
M(x)=a
Дисперсией (рассеивание значений вокруг CB вокруг среднего значения) СВ х называется МО квадрата отклонения случайной величины от ее мат. ожидания.
D(x)=M(x-a)2 (1)
Используя свойства МО ф-ла (1), можно преобразовать к виду более удобному для вычислений
D(x)=M(x)2 _ (a)2
Запишем ф-лы (1) и (2) для дискретной CB x:
1. D(x)= ∑ (xi-a)2*pi (1i)
D(x)= ∑ xi2*pi - a2 (2i)
2. для непрерывной CB x:
D(x)= ∫ (x-a)2*d(x)dx (1ii)
|
|
|
D(x)= ∫ x2*f(x)dx-a2 (2ii)
Свойства дисперсии:
- D(С)=0
- D(С*x)= c2 * D(x)
- D(x_+y)= D(x)+ D (y)
- D(x+c)= D(x)
среднее квадратическое отклонение CB Х называется корень квадратный из дисперсии этой CB Х;
δ (х)=√ D(x)
Начальный и центральный моменты
Начальным моментом порядка K CB X называется МО величины xk=M(xk)*vk
Замечание: Если К=1, то нач. момент первого порядка v1=M(x)
К=2, то нач. момент первого порядка v2=M(x2)
а)для ДСВ vk =∑ xik * pi
б)для НСВ vk =∫ xik *f(x)dx- ak
Центральным моментом порядка K CB X называется МО величины (x-M(xk))
Мk=[(x-M(x))k]
Мk=М[(x-M(x))k]
Возьмем К=1, М=1, тогда
К=1, М1=М[(x-M(x))]=0
K=2, М2=М[(x-M(x))2]*D(xk)
Замечание:
а) для ДСВ Мk =∑ (xi –а)* pi
б) для НСВ Мk =∫ (x-а)k *f(x)dx
коэффициентом ассиметрии (скошенности) CB X наз-ся число А, равное отношению центрального момента к кубу среднего квадратического отклонения А = m3/q3(x)
коэффициентом эксцесса (островершинности) наз-ся число
Е = m4/q4(x) - 3
Модой ДСВ X (М0(х)) наз-ся наиболее вероятное значение CB X
Модой НСВ Х (М0(х)) с плотностью f(x) наз-ся значение CB X, при котором функция f(x) достигает максимума.
Медианой CB X (МL(х))наз-ся такое значение CB X (xp), для которого одинаково вероятно, что CB X примет значение < xp или > xp
P{x < xp }= P{x > xp }=½
|
|
|


