 |
34. Основные понятия о разрешимых и неразрешимых проблемах. Алгоритмы и разрешимость.
|
|
|
|
34. Основные понятия о разрешимых и неразрешимых проблемах. Алгоритмы и разрешимость.
Алгоритм - точное предписание, которое задает вычислительный процесс ( алгоритмический), начинающийся с некоторого исходного данного (из совокупности возможных для данного алгоритма исходных данных) и направленный на получение полностью определяемого этим исходным алгоритмом результата.
Свойства алгоритма:
1)массовость - применимость к классу задач
2)дискретность – четкое разбиение на отдельные этапы (шаги)
3)детерминированность - четкие правила перехода от одного этапа к другому
4)конечность
Неразрешимые алгоритмические проблемы встречаются:
- в алгебре (проблема тождества для полугрупп и групп( в 1947 году независимо Марковым и Постом); группы с неразрешимой проблемой тождества - в 1952 году П. С. Новиковым;
- в топологии (проблема гомеоморфии, неразрешимость важного класса случаев 1958 г. Марков);
- в теории чисел (проблема разрешимости диофантовых уравнений- 1970 Матиясевичем) и т. д.
Рассмотрим основные методы вычисления задач.
Тезис Чёрча — Тьюринга и алгоритмически неразрешимые массовые проблемы
Тьюринг высказал предположение, что любой алгоритм может быть представлен эквивалентной машиной Тьюринга, что открыло возможности для строгого доказательства алгоритмической неразрешимости различных массовых проблем (то есть проблем о нахождении единого метода решения некоторого класса задач, условия которых могут варьироваться в известных пределах). Простейшим примером явл. проблема применимости алгоритма (проблемой остановки): требуется найти общий метод, который позволял бы для произвольной машины Тьюринга (заданной посредством своей программы) и произвольного начального состояния ленты этой машины определить, завершится ли работа машины за конечное число шагов, или же будет продолжаться неограниченно долго.
|
|
|
Устройство машины Тьюринга: бесконечная в обе стороны лента (или несколько бесконечных лент), разделённая на ячейки, и управляющее устройство, способное находиться в одном из множества состояний (число которых конечно и точно задано).
Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки ленты символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех, на которых записаны входные данные.
Управляющее устройство работает согласно правилам перехода. Каждое правило предписывает машине, в зависимости от текущего состояния и текущего символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Терминальное состояние - означает конец работы, остановку алгоритма.
Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует правило, и недетерминированной в противном случае.
Разрешимая задача – это задача, для которой может быть построена детерминированная машина Тьюринга.
Нормальные алгоритмы Маркова предназначенными для применения к словам в различных алфавитах. Состоит из двух частей: определения алфавита алгоритма и определения его схемы. Схемой нормального алгоритма называется конечный упорядоченный набор т. н. формул подстановки, каждая из которых может быть простой или заключительной. Простыми формулами подстановки называются слова вида L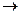 
D, где L и D — два произвольных слова в алфавите алгоритма (называемые, соответственно, левой и правой частями формулы подстановки). Аналогично, заключительными формулами подстановки называются слова вида L 
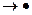D, где L и D — два произвольных слова в алфавите алгоритма. При этом предполагается, что вспомогательные буквы и не принадлежат алфавиту алгоритма (в противном случае на исполняемую ими роль разделителя левой и правой частей следует избрать другие две буквы).
|
|
|
Любой нормальный алгоритм эквивалентен некоторой машине Тьюринга, и наоборот — любая машина Тьюринга эквивалентна некоторому нормальному алгоритму. Вариант тезиса Чёрча — Тьюринга, сформулированный применительно к нормальным алгоритмам, принято называть «принципом нормализации».
Машина Поста. состоит из каретки (или считывающей и записывающей головки) и разбитой на секции бесконечной в обе стороны ленты. Каждая секция ленты может быть либо пустой — 0, либо помеченной меткой 1. За один шаг каретка может сдвинуться на одну позицию влево или вправо, считать, поставить или уничтожить символ в том месте, где она стоит. Работа МП определяется программой, состоящей из конечного числа строк. Всего команд шесть: N. → J(сдвиг вправо); N. ← J (сдвиг влево); N. 1 J (запись метки); N. 0 J(удаление метки); N. ? J1, J0 (условный переход по метке); N. Stop(остановка), где N. — номер строки, J — строка на которую переходит управление далее.
Для работы машины нужно задать программу и ее начальное состояние (т. е. состояние ленты и позицию каретки). После запуска возможны варианты:
· работа может закончиться невыполнимой командой (стирание несуществующей метки или запись в помеченное поле);
· работа может закончиться командой Stop;
· работа никогда не закончится.
|
|
|
