 |
48.Упрощение игр.. 49.Игра 2 на 2.
|
|
|
|
48. Упрощение игр.
Если платежная матрица игры не содержит седловой точки, то задача определения оптимальной смешанной стратегии тем сложнее, чем больше размерность матрицы. Поэтому для игр с платежными матрицами большой размерности отыскание решения можно упростить, если уменьшить их размерность путем вычерчивания дублирующих изведомо невыгодных стратегий, а также замены некоторых групп чистых стратегий смешанными
Если в матрице A=|| aij || игры все элементы строки(столбца) равны соответствующим элементам другой строки(столбца), то соответствующие строкам(столбцам) стратегии называются дублирующими.
Если в матрице A=|| aij || игры все элементы некоторой строки определяют стратегию xi игрока I не больше соответсвующих элементов другой строки, то стратегия xi называется заведомо невыгодной.
Если в матрице A=|| aij || игры все элементы некоторого столбца, определяющие стратегию yi игрока II не меньше соответствующих элементов другого столбца, то стратегия yi называется заведомо невыгодной.
| 1 2 4 3 1 | x1
A= | 0 2 3 2 1 | x2
| 1 2 4 3 1 | x3
| 4 3 1 0 1 | x4
y1 y2 y3 y4 y5
стратегия x3 дублирует стратегию x1, поэтому любую из них можно вычеркнуть.
Если сравнить x1 и x2, то можно заметить, что все элементы x2 не превышают соответствующих элементов x1. Значит стратегия x2 для нас, желающих выиграть заведомо невыгодна. Вычеркивая x3 и x2 приведем матрицу к более простому виду.
| 1 2 4 3 |
A= | 4 3 1 0 |
Для второго игрока стратегия y3 заведомо невыгодна. Вычеркивая ее получим
| 1 2 3 |
A= | 4 3 0 |
49. Игра 2 на 2.
|
|
|
В игре нет седловой точки, то обе стратегии игроков являются активными. Если 2-ой игрок применяет стратегию B1, то выигрыш первого игрока определяется из уравнения
a11 p1 +a21 p2 = t если 2 применяет B2, то выигрыш 1 a12 p1 +a22 p2 = t, т. к. p1+p2=1, то получим систему решений S1* = (p1*, p2*) аналогично для второго игрока
| a11 a12 | A1
A= | a21 a22 | A2
B1 B2

В системе координат на оси абсцисс отложим от начала координат отрезок длинной равной единице.
Левый конец отрезка соответствует стратегии A1, а правый (x = 1) – стратегии A2. Все промежуточные точки отрезка будут изображать смешанные стратегии A1 игрока. Длина отрезка SA A2 равна вероятности p1 стратегии A1. Длина SA A2 равна p1 стратегии A2. Через A1 и A2 проведем два перпендикуляра к оси абсцисс – ось I-I и ось II-II. На I-I будем откладывать выигрыш при стратегии A1, а на II-II – при A2. Если игрок 2 применит стратегию B1, то при A1 выигрыш равен a11, а при A2 равен a21. Отложим эти точки на осях I-I и II-II и обозначим их B1. , что соответствует одноименной стратегии 2-го игрока. Любой смешанной стратегии SA=(p1*p2) соответствует выигрыш, величина которого равна абсциссе точки М на прямой B1B2. Эту прямую будем называть стратегией B1. Аналогично можно построить стратегию B2. Задача состоит в определении оптимальной стратегии S(со*)A, при которой наш минимальный выигрыш обращался бы в максимум. Построим нижнюю границу выигрыши при стратегиях B1, B2, т. е. ломанную B1MB2. На этой ломанной будет лежать минимальный выигрыш A при любой смешанной стратегии. В точке М имеем максимальную цену игры t.
Пример
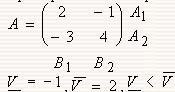

50. Игры 2 на n и m на 2.
В играх порядка 2 x m первый игрок имеет две стратегии, а второй – m стратегий. Платежная матрица имеет вид:
| a11 a12 … a1m |
A= | a21 a22 … a2m |
Причем у нее нет седловых точек.
Необходимо найти такие смешанные стратегии x=S1=(p1*p2) и S2=q1, …, qm и цену игры gamma, которые удовлетворяют соотношениям
|
|
|
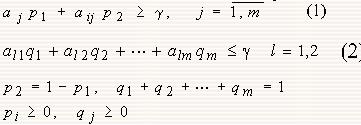
Что означают неравенства (1) и (2). Пусть игрок 1 применяет свою оптимальную стратегию S1* а его противник применяет чистую стратегию yj. Т. к. это цена игры gamma, то она определяет нижний придел выигрыша при любых стратегиях второго игрока, в том числе смешанных. Аналогично можно объяснить неравенство (2) – верхний предел проигрыша 2-го игрока. Не доказывая, отметим, что любая конечная игра m x n имеет решение, в котором число активных стратегий каждого игрока не превосходит min(m, n). Следовательно, у игры 2 x m или n x 2 всегда имеется решение, содержащее не более двух активных стратегий у каждого из игроков. Если найти эти активные стратегии игроков, то игра 2 x m или n x 2 превращается в игру 2x2.
Введем обозначение для левой части неравенств (1)
Mj(p1) = a1j*p1 + a2j *p2 = a1j*p1 + a2j(1-p1)=(a1j-a2j)*p1+a2j j=1, m, где Mj(p1) – средний выигрыш первого игрока при условии, что он применяет свою смешанную стратегию, а второй – свою j чистую стратегию. Каждому значению j=1, m соответствует прямая линия прямоугольной системы координат.
Цель второго игрока минимизировать выигрыш первого за счет своих альтернатив. Поэтому 2 игрок должен определить такие j, которые обеспечивают min Mj(p1) = M(p1), где M(p1) – нижняя граница множества ограничений (показана жирной линий).

Цель первого игрока максимизировать свой выигрыш за счет выбора p1, т. е. вычислить max M(p1)=gamma.
В результате определяется оптимальная стратегия первого игрока S1*=(p1*, 1-p1*) и пара альтернативных стратегий 2 игрока, которые при пересечение образуют точку M0. В нашем случае это y1 и y5. В результате мы свели задачу размерности 2 x m, к задаче 2 x 2 с платежной матрицей
| a11 a15 |
A= | a21 a25 |
Решая полученную игру найдем S1*=(p1*, p2*) и S1*=(q1*, q2*)
|
|
|


