 |
51.Марковский процесс с дискретными состояниями и дискретным временем
|
|
|
|
51. Марковский процесс с дискретными состояниями и дискретным временем
Случайный процесс называется процессом с дискретным временем, если переходы системы S из состояния в состояние возможны только в строго определенные моменты времени t1, t2, …. В промежутки времени между этими моментами система сохраняет свое состояние.
Процесс, происходящий в системе, можно представить как последовательность событий, например: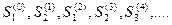 
Такая случайная последовательность событий называется марковской цепью.
Мы будем описывать марковскую цепь с помощью так называемых вероятностей состояний. Пусть после k-ого шага система S может быть в одном из состояний S1, S2, …, Sn, т. е. осуществится одно из полной группы несовместных событий: 
.
Обозначим вероятности этих событий:
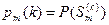
( короче: вероятность того, что после k-го шага система перейдёт в m-е состояние равна вероятности m-го события на k-м шаге )
Будем называть вероятности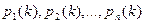 
вероятностями состояний. Найдем эти вероятности для любого k.
Марковская цепь называется однородной, если переходные вероятности не зависят от номера шага. В противном случае марковская цепь называется неоднородной.
Обозначим pij вероятность перехода системы S за один шаг из состояния Si в состояние Sj. Эти вероятности можно записать как условные вероятности pij.
Из вероятностей pij можно составить матрицу
,
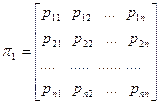которая называется матрицей перехода за один шаг. Сумма элементов каждой строки равна единице.
Обозначим pij(k) вероятность перехода системы S из состояния Si в состояние Sj за k шагов. Обозначим через pk матрицу перехода через k шагов
Согласно между матрицами перехода с различными индексами существует соотношение pk =pl pk-l (0< l< k). В частности, при k=2 находим, что 
при k=3 
и вообще при любом k 
|
|
|
Теорема Маркова. Если при некотором S> 0 все элементы матрицы 
положительны, то существуют такие постоянные числа pj (j=1, 2, 3, …, n) что независимо от индекса i имеют место равенства
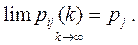
Величины pj называются финальными вероятностями системы S.
52. Марковский процесс с дискретными состояниями и непрерывным временем.
Имеется система S, которая в каждый момент времени может находиться в одном из состояний S1, S2, …, Sn. Переход системы из одного состояния в другое может осуществляться в любой момент времени. Такой процесс называется непрерывной цепью Маркова.
Обозначим pi(t) – вероятность того, что в момент времени t система S будет находиться в состоянии Si (i=1, 2, …, n). Для любого момента времени
.
Поставим задачу – определить для любого t вероятность состояний: p1(t), p2(t), …, pn(t). Будем считать, что известны плотности вероятностей перехода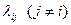 
. Пусть 
- вероятность перехода системы S из состояния Si в состояние Sj за время 
. Тогда
Тогда с точностью до бесконечно малых высших порядков
Если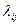 
не зависят от t, Марковский процесс называется однородным, если зависят – то неоднородным. Вероятности 
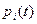удовлетворяют следующей системе дифференциальных уравнений:
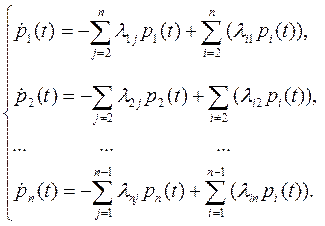
Эти уравнения для вероятностей состояний называются уравнениями Колмогорова. Для однозначного решения системы должны быть заданы начальные значения: p1(0), p2(0), …, pn(0), причем
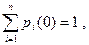
Предположим, что
где pi финальные вероятности. Чтобы их найти в системе положим 
. Тогда будем иметь следующую систему линейных алгебраических уравнений
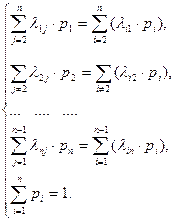. (7)
Здесь n+1 уравнение с n неизвестными. Поэтому одно из однородных уравнений можно отбросить.
|
|
|
