 |
53.Система массового обслуживания с отказами.
|
|
|
|
53. Система массового обслуживания с отказами.
В таких системах заявка, поступившая в момент, когда все каналы заняты, немедленно получает отказ, покидает систему и в дальнейшем процессе обслуживания не участвует.
Пусть имеется n канальная система массового обслуживания с отказами. Рассмотрим ее как физическую систему Х с конечным множеством состояний:
x0 – свободны все каналы,
x1 – занят ровно один канал,
……………………………..
xn – заняты все n каналов.
Требуется определить вероятности состояний системы 
(k=0, 1, 2, …, n) для любого момента времени t. Задачу решить при следующих допущениях:
1). Поток заявок – простейший с плотностью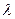 
;
2). Время обслуживания Тоб - показательное с параметром 
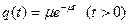
Процесс, протекающий в системе, будет Марковским.
Вероятности 
удовлетворяют следующим уравнениям Эрланга:
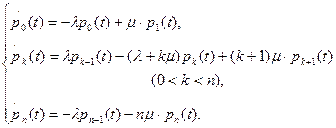
Для любого момента времени должно выполняться условие
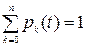
Вероятность характеризует среднюю загрузку системы и ее изменение с течением времени.
Величина 
называется относительной пропускной способностью системы. Для данного момента t это есть отношение среднего числа обслуженных за единицу времени заявок к среднему числу поданных.
54. Система массового обслуживания с ограничением по длине очереди.
(Система массового обслуживания смешанного типа)
Рассмотрим смешанную систему массового обслуживания Х с n каналами при следующих условиях. На вход системы поступает простейший поток заявок с плотностью 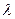. Время обслуживания одной заявки Тоб - показательное с параметром 
. Заявка, заставшая все каналы занятыми, становится в очередь и ожидает обслуживания при условии, что длина очереди меньше m. Если же число заявок в очереди равна m (больше m оно быть не может), то последняя прибывшая заявка в очередь не становится и покидает систему не обслуженной.
|
|
|
Заявку будем называть « связанной с системой », если она либо находится в состоянии обслуживания, либо ожидает очереди. Возможные состояния будут
x0 – ни один канал не занят,
xk – занято ровно k каналов (1 
x n),
xn+s – заняты все n каналов. s заявок стоят в очереди. (1 ≤ s ≤ m).
Число заявок s, стоящих в очереди, не может быть больше m. Соответственно, число описывающих ее дифференциальных уравнений равно n+m+1. Они имеют вид:
(2)
 |
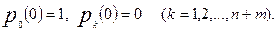Начальными условиями являются:
Вероятность того, что заявка покинет систему необслуженной, равна pn+m. Относительная пропускная способность системы определяется формулой
.
55. Исчисление высказываний
Напомним, что тавтологией мы называли пропозициональную формулу, истинную при всех значениях переменных. Оказывается, что все тавтологии можно получить из некоторого набора " аксиом" с помощью " правил вывода", которые имеют чисто синтаксический характер и никак не апеллируют к смыслу формулы, ее истинности и т. д. Эту задачу решает так называемое исчисление высказываний.
Одним из возможных вариантов (Гильбертовской) аксиоматизации логики высказываний является следующая система аксиом (Каковы бы ни были формулы 
, следующие формулы называют аксиомами исчисления высказываний):
;
;
;
;
;
;
;
;
;
;
.
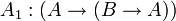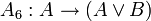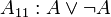вместе с единственным правилом:
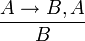(Modus ponens)
Теорема корректности исчисления высказываний утверждает, что все перечисленные выше аксиомы являются тавтологиями, а с помощью правила modus ponens из истинных высказываний можно получить только истинные. Доказательство этой теоремы тривиально и сводится к непосредственной проверке. Куда более интересен тот факт, что все остальные тавтологии можно получить из аксиом с помощью правила вывода — это так называемая теорема полноты логики высказываний.
|
|
|
Несложно проверить, что все аксиомы — тавтологии. Для примера проделаем это для самой длинной аксиомы (точнее, схемы аксиом) — для второй. В каком случае формула
(где — некоторые формулы) могла бы быть ложной? Для этого посылка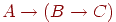 
должна быть истинной, а заключение 
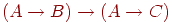— ложным. Чтобы заключение было ложным, формула 
должна быть истинной, а формула 
— ложной. Последнее означает, что 
истинна, а 
ложна. Таким образом, мы знаем, что , 
и 
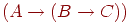истинны. Отсюда следует, что 
и 
истинны, и потому истинна — противоречие. Значит, наша формула не бывает ложной.
Корректность правила MP также очевидна: если формулы и всегда истинны, то по определению импликации формула также всегда истинна. Таким образом, все формулы, входящие в выводы (все теоремы) являются тавтологиями.
Теорема (О корректности ИВ). Всякая теорема исчисления высказываний есть тавтология.
Теорема (О полноте ИВ). Всякая тавтология есть теорема исчисления высказываний.
Теорема (корректность исчисления высказываний, вторая форма). Всякое совместное множество формул непротиворечиво.
Теорема (полнота исчисления высказываний, вторая форма). Всякое непротиворечивое множество совместно.
Теорема (теорема компактности для исчисления высказываний). Пусть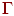 
— множество формул, всякое конечное подмножество которого совместно. Тогда и все множество 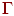совместно.
Теорема 22 (лемма Кенига). Любое бесконечное дерево имеет бесконечную ветвь.
Говоря о бесконечности дерева, мы имеем в виду, что соответствующее множество бесконечно. Отсюда следует, что оно содержит слова сколь угодно большой длины.
Обычно утверждение леммы Кенига формулируют так: если колония бактерий, возникшая из одной бактерии, никогда не вымирает полностью, то существует бесконечная последовательность бактерий, каждая следующая из которых получается при делении предыдущей.
|
|
|
