57.Логика предикатов первого порядка

Логика первого порядка (исчисление предикатов) — формальное исчисление, допускающее высказывания относительно переменных, фиксированных функций, и предикатов. Расширяет логику высказываний. В свою очередь является частным случаем логики высшего порядка.

Определение (логики высшего порядка). Пусть М – непустое множество. Тогда n-местным предикатом, заданным на М, называется выражение, содержащее n переменных и обращающееся в высказывание при замене этих переменных элементами множества М.

Рассмотрим примеры. Пусть М есть множество натуральных чисел N. Тогда выражения «x – простое число», «x – четное число», «x – больше 10» являются одноместными предикатами. При подстановке вместо x натуральных чисел получаются высказывания: «2 – простое число», «6 – простое число», «3 – четное число», «5 больше 10» и т. д. Выражения «x больше y», «x делит y нацело», «x плюс y равно 10» являются двухместными предикатами. (Конечно, последнее выражение можно было записать и так: «x+y=10»). Примеры трехместных предикатов, заданных на множестве натуральных чисел: число z лежит между «x и y», «x плюс y равно z», «|x-y|£ z».

Будем считать, что высказывание – нульместный предикат, то есть предикат, в котором нет переменных для замены.

Предикат с заменяемыми переменными x₁, …, x_n будет обычно обозначаться заглавной латинской буквой. После которой в скобках указаны эти переменные. Например, P(x₁, x₂), Q(x₂, x₃), R(x₁). Среди переменных в скобках могут быть и фиктивные.

Определение. Предикат W(x₁, …, x_n) называется конъюнкцией предикатов U(x₁, …, x_n) и V(x₁, …, x_n), заданных на множестве М, если для любых а₁, …, а_n из М высказывание W(а₁, …, а_n) есть конъюнкция высказываний U(а₁, …, а_n) и V(а₁, …, а_n).

Легко по аналогии привести определения и других упомянутых выше операций.

В логике предикатов первого порядка вводятся и две новые операции: квантором общности и квантором существования. Эти операции рассмотрим вначале на примерах. Пусть дано выражение «существует х такой, что x+y=10». На множестве натуральных чисел это предложение определяет одноместный предикат P(y), так Р(2) и Р(9) – истинные высказывания, Р(11) – ложное. Если обозначить предикат «x+y=10» через S(x, y) (а это предикат двухместный), то P(y) можно записать так: «существует х такой, что S(x, y)». В этом случае говорят, что предикат P(y) получен из предиката S(x, y) навешиванием квантора существования на x и пишут P(y)=($x)S(x, y). Рассмотрим другой пример. Выражение «для всех х справедливо, что y³ -х²» определяет на множестве целых чисел одноместный предикат Q(y). Если предикат «y³ -х²» обозначить через T(x, y), то Q(y) можно записать так: «для всех x справедливо T(x, y)». В таком случае говорят, что предикат Q(y) получен из предиката T(x, y) навешиванием квантора общности на х и пишут Q(y)=(" x)T(x, y).

Определение. Пусть P(x₁, …, x_n) – предикат, заданный на множестве M, y – переменная. Тогда выражение «для всякого y выполняется P(x₁, …, x_n)» – предикат, полученный из P навешиванием квантора общности на переменную y, а выражение «существует y такой, что выполняется P(x₁, …, x_n)» – предикат, полученный из P навешиванием квантора существования на переменную y.

Язык логики первого порядка строится на основе сигнатуры, состоящей из множества функциональных символов 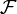и множества предикатных символов 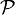. С каждым функциональным и предикатным символом связана арность, то есть число возможных аргументов. Допускаются как функциональные так и предикатные символы арности 0. Первые иногда выделяют в отдельное множество констант. Кроме того используются следующие дополнительные символы

• Символы переменных (обычно x, y, z, x₁, y₁, z₁, x₂, y₂, z₂, и т. д. ),
• Пропозициональные связки: 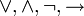, (конъюнкция, дизъюнкция, отрицание, импликация и эквиваленция)
• Кванторы: всеобщности 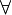и существования ,
• Служебные символы: скобки и запятая.

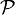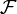Перечисленные символы вместе с символами из и образуют Алфавит логики первого порядка. Более сложные конструкции определяются индуктивно:

• Терм есть символ переменной, либо имеет вид , где f — функциональный символ арности n, а 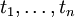— термы.
• Атом имеет вид , где p — предикатный символ арности n, а 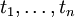— термы.
• Формула — это либо атом, либо одна из следующих конструкций: 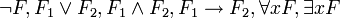, где F, F₁, F₂ — формулы, а x — переменная.

Переменная x называется связанной в формуле F, если F имеет вид 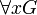либо 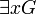, или же представима в одной из форм , причем x уже связанна в H, F₁ и F₂. Если x не связанна в F, ее называют свободной в F. Формулу без свободных переменных называют замкнутой формулой, или предложением. Теорией первого порядка называют любое множество предложений.

Логика первого порядка обладает рядом полезных свойств, которые делают ее очень привлекательной в качестве основного инструмента формализации математики. Главными из них являются полнота (это означает, что для любой формулы выводима либо она сама, либо ее отрицание) и непротиворечивость (ни одна формула не может быть выведена одновременно со своим отрицанием). При этом если непротиворечивость более или менее очевидна, то полнота — нетривиальный результат полученный Гёделем в 1930 году (теорема Гёделя о полноте). По сути теорема Гёделя устанавливает фундаментальную эквивалентность понятий доказуемости и общезначимости.

Логика первого порядка обладает свойством компактности: если некоторое множество формул не выполнимо, то невыполнимо также некоторое его конечное подмножество.

Являясь формализованым аналогом обычной логики, логика первого порядка дает возможность строго рассуждать об истинности и ложности утверждений и об их взаимосвязи, в частности, о логическом следовании одного утверждения из другого, или, например, об их эквивалентности. Рассмотрим классический пример формализации утверждений естественного языка в логике первого порядка.

Возьмем рассуждение «Каждый человек смертен. Конфуций — человек. Следовательно, Конфуций смертен». Обозначим «x есть человек» через ЧЕЛОВЕК (x) и «x смертен» через СМЕРТЕН (x). Тогда утверждение «каждый человек смертен» может быть представлено формулой: 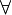x( ЧЕЛОВЕК (x) → СМЕРТЕН (x)) утверждение «Конфуций — человек» формулой ЧЕЛОВЕК ( Конфуций ), и «Конфуций смертен» формулой СМЕРТЕН ( Конфуций ). Утверждение в целом теперь может быть записано формулой

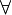x( ЧЕЛОВЕК (x) → СМЕРТЕН (x)) ЧЕЛОВЕК ( Конфуций ) → СМЕРТЕН ( Конфуций )