7.3. Автокатализ, динамика популяций

Пример 3. Рассмотрим прямую автокаталитическую реакцию - самовоспроизводство вещества Х:

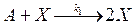
Кинетическое уравнение в. этом случае также линейное:

                                                  .                                   (7. 12)

Его решение:

                                      .                             (7. 13)

Об этом же свидетельствует рассмотрение данной системы с помощью потенциала:

                                                                                                (7. 14)         

В дальнейшем мы будем рассматривать нелинейные системы.

Пример 4. Рассмотрим реакцию примера 3, но в замкнутом объёме - это означает, что хотя компонент А постепенно переходит в компонент Х, их суммарное количество остаётся неизменным, т. е С_А + С_х = С₁ = const. Тогда концентрация компонента А будет равна С_А = С₁ - С_х, и кинетическое уравнение примет виде:

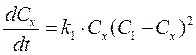                                                                               (7. 15)       

Это уравнение, как мы видим, уже нелинейно, так как искомая концентрация входит в него во второй степени. Стационарных состояний также два: первое Сх= С₁, второе Сх=0. Решение уравнения можно получить в явном виде, если перейти к новым переменным  х = С_х/С₁ £ 1 и t= tk₁c₁, тогда:

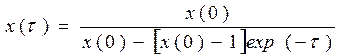                                          (7. 16)

Исследование данного случая с помощью потенциала состоит в следующем. Потенциал имеет вид:

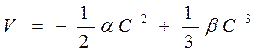                                        ,                  (7. 17) 

где a и b всегда положительны, т. к. представляет собой комбинацию положительных по определению величин k₁, k_-1, С_А, С₁. Графическое изображение потенциала на рис. 7. 3 показывает, что при любых изменениях параметров a и b форма потенциальной кривой остаётся неизменной, т. е. на ней всегда есть один минимум, отвечающий устойчивому стационарному состоянию, и один максимум, соответствующий неустойчивому стационарному состоянию - неустойчивым является стационарное состояние при нулевой концентрации компонента Х, так как здесь находится вершина холма:

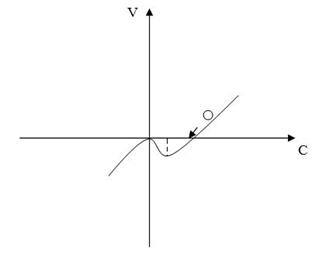
Рис. 7. 3. Общий вид потенциала для нелинейных автокаталитических реакций.

Пример 5. Рассмотрим автокатализ вместе с обратной реакцией (тоже нелинейная система):

                                                                 A + X ↔ 2X                                                               

Соответствующее кинетическое уравнение имеет вид:

                                                                         (7. 18)

аналогичный предыдущему случаю. Стационарных состояний также два -  и С_х = 0. Решение можно получить в том же виде, что и в предыдущем примере, если положить х = С_х/С₂ и t = tк₁С_А. Таким образом, анализ этой системы с помощью потенциала полностью аналогичен  примеру 4.

Пример 6. Рассмотрим динамику популяций, т. е закономерность изменения числа особей животных или растений данного вида при заданных внешних природных условиях. Пусть число особей равно N, и данная популяция возрастает по закону dN/dt^. = RN, т. е чем больше особей, тем быстрее они размножаются. Показатель роста R в общем случае зависит от числа особей: например, при постоянных запасах пищи в окружающей среде R будет уменьшаться с ростом N, поскольку пищи на каждого становится меньше. Закон, по которому меняется R, обычно описывается уравнением типа

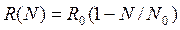                                           ,                                (7. 19)        

где R₀ и N₀ - константы. Тогда модель развития популяции запишется следующим образом:

                                                                                  (7. 20)

Это уравнение называется законом Ферхлюста-Перла. Уравнение полностью совпадает с кинетическим уравнением реакций из примеров 4 и 5, если х = N/N₀ и t = Rt - соответственно, все выводы, полученные нами для рассмотренных в указанных примерах химических реакций, можно перенести на динамику популяций в модели Ферхлюста-Перла. Отсюда можно сделать важный вывод: одна и та же динамическая модель может описывать поведение самых различных по своей природе систем.