 |
Динамические уравнения процессов с одной переменной.
|
|
|
|
Динамические уравнения процессов с одной переменной.
Рассмотрим несколько простых неравновесных процессов из механики и химии, на примере которых можно сделать некоторые общие выводы относительно динамики их развития.
Рассмотрим систему, в которой частица массой m ускоряется под действием силы F0
, (7. 2)
где q - координата. Силу F0 можно представить с помощью силы трения, которая
пропорциональна скорости, и включает в себя движущую силу:
(7. 3)
Тогда уравнение движения приводится к виду:
, (7. 4)
причём сила F(q) во многих случаях оказывается зависимой от координаты. Последнее уравнение - это динамическая модель движения частицы с учётом трения. Исследуем поведение этой модели во времени. Если m мало, а постоянная трения g велика, то можно пренебречь первым членом в уравнении движения по сравнению со вторым - это случай так называемого передемпфированного ангармонического движения. Если ввести здесь новый масштаб времени t = gt, то уравнение движения перепишется в следующем виде:
, 
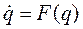, (7. 5)
Уравнения такого вида встречаются во многих дисциплинах - например, в химии при описании реакции А + В ® С, где скорость изменения концентрации вещества С определяется системой:
, 
, (7. 6)
|
|
|
где СА, СВ - концентрации компонентов А и В, k - константа скорости реакции.
В механике аналогично получим для гармонического осциллятора:
, 
. (7. 7)
Поэтому принимаем это уравнение в качестве основной модели для изучения поведения систем с одной переменной. Дальнейшее исследование поведение этой модели во времени может быть осуществлено тремя способами: решение самих уравнений модели, исследование поведения потенциальной функции модели и анализа поведения модели вблизи стационарного состояний. Решение уравнений является предпочтительным, но это не всегда возможно, тогда для исследования поведения модели используют её потенциальную функцию (потенциал). Системы, которые позволяют построить потенциал, называются градиентными. Если же система не градиентная, то используют третий путь исследования.
7. 2. Эволюция систем – метод потенциала
В данном разделе мы будем рассматривать только градиентные системы. Будем считать, что модель градиентная, и проанализируем её с помощью потенциала, для чего введём понятие потенциала – функции V(q):
, 
(7. 8)
В механике потенциал - это работа перемещения тела в поле силы F, взятая с обратным знаком. Понятие потенциала пригодится нам не только в механике, при этом следует учитывать, что его физическая трактовка не всегда будет столь наглядной, как в механике. Используем вначале понятие потенциала для анализа линейных механической и химической систем, а затем перейдём к нелинейным моделям.
Пример 1. Проанализируем с помощью потенциала состояние равновесия линейной механической системы - гармонического осциллятора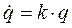 
. В соответствии с определением, потенциал в данном случае запишется следующим образом 
.
|
|
|
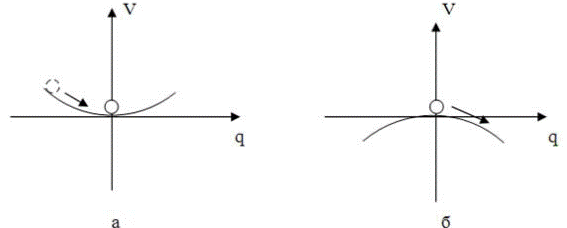
Рис. 7. 1. Механический потенциал гармонического осциллятора: а – k > 0; б - k < 0
Кривая потенциала представляет собой параболу, которая при k > 0 находится в положительной полуплоскости, а при к< 0 - в отрицательной, что показано на рис. 7. 1. При k > 0 реализуется устойчивое состояние равновесия - система-шарик скатывается на дно оврага и остаётся там неограниченно долго. При k < 0 состояние равновесия неустойчиво - шарик скатывается с вершины горы и уходит на бесконечность. При k = 0 происходит переход от устойчивого равновесия к неустойчивому (или наоборот).
Графически зависимость равновесного значения координаты qe от константы k показана на рис. 7. 2. При k > 0 устойчивому равновесию соответствует нулевое значение координаты qe = 0 (на рисунке в правой полуплоскости нулевое значение qe выделено двумя сплошными линиями вблизи оси абсцисс). При k < 0 равновесие неустойчивое (qe по-прежнему равно нулю, но чтобы показать, что равновесие неустойчивое, на рисунке в левой полуплоскости оно выделено двумя пунктирными линиями):
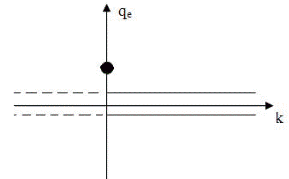
Рис. 7. 2. Диаграмма зависимости равновесных значений координаты от постоянного параметра k.
Пример 2. Проанализируем протекание реакции разложения и производства компонента X (линейная система):
A ↔ X
Тогда скорость изменения концентрации компонента Х - dCx/dt можно определить из кинетического уравнения:
(7. 9)
где СА, Сх - концентрации веществ А и Х соответственно (в дальнейшем нижний индекс при концентрации будет указывать, о каком веществе идёт речь), Ф - приток компонента Х в систему (химическая система открыта), k1 и k-1 – константы скоростей прямой и обратной реакций. Если Ф постоянен, то стационарное состояние находим, приравняв dCx/dt к нулю. Обозначив значение концентрации, соответствующее стационарному состоянию, через С0 и решив стационарное кинетическое уравнение, получим:
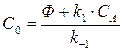(7. 10)
|
|
|
Для исходного уравнения легко получить общее решение, которое будет выглядеть следующим образом:
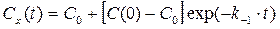, (7. 11)
где Сх(0) - концентрация компонента Х в начальный момент времени.
Как и для гармонического осциллятора, для анализа данной реакции можно построить потенциал. Так как приведённое уравнение аналогично уравнению гармоничного осциллятора, то потенциал в этом случае будет иметь тот же вид – его отличие лишь в том, что, поскольку k-1 всегда положительно, то случай, соответствующий рис. 7. 1б, не реализуется, а значит, стационарное состояние С0 всегда будет устойчивым. Таким образом, исследование линейной системы химической реакции 
с помощью потенциала подтверждает вывод термодинамики линейных процессов: стационарное состояние в системе единственное и устойчивое.
|
|
|
