7.4. Автокатализ с ветвлением, бифуркации – неравновесные фазовые переходы

Пример 7. Рассмотрим автокаталитическую реакцию с ветвлением, то есть такая реакция имеет две стадии:

1) A + X ↔ 2X;                                                      

2) .                                                  

Таким образом, суммарная реакция представляет собой превращение исходного вещества А в конечный продукт В: А ®  В, а приток вещества Х отсутствует. Кинетическое уравнение в этом случае имеет вид:

                                                                 (7. 21)

Не решая уравнения, проанализируем систему методом потенциала - н будет, как и в примере 5, содержать квадратичный и кубический члены:

                                           (7. 22)

При анализе этого потенциала, в отличие от всех ранее рассмотренных примеров, обнаруживаются два возможных пути протекания процесса. При С_А > k₂/k₁ форма потенциала будет такой, как это показано на рис. 7. 4а: на кривой два экстремума - минимум, отвечающий устойчивому стационарному состоянию при С₁= (k₁С_А-k₂)/k_-1, и максимум - неустойчивое стационарное состояние при С₂=0:

Рис. 7. 4. Потенциал для реакции автокатализа с ветвлением: а - , б - , в - .

При С_А < k₂/k₁ кривая потенциала рис. 7. 4б сдвинута влево так, что минимум - устойчивое стационарное состояние - расположен теперь при С₂=0, а максимум находится  в области отрицательных концентраций, т. е не имеет физического смысла.

Переход от одного пути к другому происходит при критической концентрации С_А^кр = k₂/k₁, когда максимум и минимум сливаются в нуле в одну точку перегиба на рис. 7. 4в. Концентрация С_А является критической в том смысле, что по разные стороны от неё кинетическое уравнение системы имеет отличающиеся друг от друга решения: вместо устойчивого стационарного состояния при С = С₂ слева от критической точки при С_А > C_A^кр появляется устойчивое состояние при С = С₁, а состояние С₂ становится неустойчивым - такая критическая точка на языке математики носит название бифуркационной, а особенность разветвления решения при переходе через критическое значение параметра - бифуркацией . Для наглядного изображения возможных состояний системы и их взаимных переходов построим зависимость стационарной концентрации х от С_А, которая называется бифуркационной диаграммой (рис. 7. 5):

Рис. 7. 5. Зависимость стационарной концентрации от параметра  (автокатализ с ветвлением): в точке С_А^кр прямая, соответствующая устойчивому стационарному состоянию, которая до этого совпадала с осью абсцисс, скачком меняет наклон - это означает, что устойчивому стационарному состоянию при
С_А > С_А^кр соответствует концентрация С_х ¹ 0. Неустойчивое стационарное состояние показано на рисунке пунктиром.

Таким образом, на основе проведённого анализа можно сделать качественные выводы относительно поведения решения модели - зависимости С_х от времени: если С_А меньше критического, то концентрация Х будет падать от начального значения до нуля, как показано выще на рисунке а, а при С_А > С_А^кр концентрация Х возрастает от начального значения до значения, соответствующего устойчивому стационарному состоянию. В точке С_А^кр, т. е. при переходе через критическое значение параметра, характер поведения системы (путь протекания реакции) меняется скачком - налицо неравновесный фазовый переход. Следовательно, бифуркация решения динамического уравнения модели соответствует неравновесному переходу в системе.

Пример 8. Рассмотрим одну из реакций металлургического производства, которая ведёт себя аналогично системе в примере 7 - такой реакцией является восстановление твёрдого вюстита газообразным оксидом углерода в присутствии твёрдого углерода (в виде кокса или угля):

                              .

Есть также реакция газификации углерода, которая приводит к увеличению содержания СО:

                                                    .                                                        

Если реакция газификации протекает быстро (не лимитирует процесс), то эту химическую систему можно представить следующим образом:

                                     .                                         

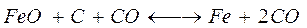Учтём дополнительно, что система открыта, т. е. газообразный СО выносится из реакционной зоны со скоростью, пропорциональной его концентрации (пусть коэффициент пропорциональности равен k₂). Тогда общая схема процесса запишется в виде:

                                                             .                                                                 

При записи кинетического уравнения этого процесса учтём также, что скорость восстановительной стадии будет зависеть не только от концентрации газообразного СО (которую обозначим как С), но и от размеров реакционной поверхности твёрдых веществ в системе вюстит-углерод, которую обозначим как S_эфф. Тогда скорость изменения концентрации СО будет равна:

                      .         (7. 23)

Полученное уравнение полностью повторяет кинетическое уравнение из примера 7, здесь здесь роль С_А играет S_эфф: при S_эфф < k₂/k₁ реакция затухает (устойчивым является стационарное состояние при нулевой концентрации), при S_эфф > k₂/k₁ реакция течёт в стационарном режиме, а неравновесный переход происходит при S_эфф = k₂/k₁, т. е. при определённых размерах реакционных поверхностей вюстита и углерода, которые находятся в твёрдом состоянии.