7.5. Ангармонический осциллятор – нарушение временной симметрии

7. 5. Ангармонический осциллятор – нарушение временной симметрии

Пример 9. Разберём модель ангармонического осциллятора, которая описывается уравнением:

                                                                                     (7. 24)       

Определим потенциал, при этом будем считать, что всегда k₁ > 0.:

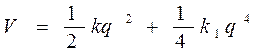                                                                (7. 25)

Здесь возможны два случая поведения системы:

k > 0, тогда потенциал - это парабола в положительной полуплоскости, и состояние q = 0 будет состоянием устойчивого равновесия (рис. 7. 7а).

k < 0, тогда потенциал имеет вид, показанный на рис. 7. 7б, т. е. в системе при q₁ и q₂ появляются два равноценных состояния устойчивого равновесия, а при q=0 (вершина холма) - неустойчивое равновесие:

Рис. 7. 6. Потенциал для ангармонического осциллятора: а - k > 0, б - k < 0.

Найти q₁ и q₂ можно, приравняв dq/dt нулю и решив полученное алгебраическое уравнение:

                                                 .                            (7. 26)

Если построить зависимость равновесной координаты q_e от k (бифуркационную диаграмму), то она будет иметь вид «вилки», показанный на рис. 7. 7: единственное в правой полуплоскости равновесное значение, равное нулю, при k = 0 раздваивается, и в левой полуплоскости имеются две ветви q_e, расходящиеся с ростом k. Разветвление решения, происходящее в бифуркационной точке при k = 0, можно проиллюстрировать схемой, которая называется бифуркационной диаграммой:

Рис. 7. 7. Зависимость равновесного значения переменной для ангармонического осциллятора от параметра k.

Что же происходит с системой при бифуркации? По мере приближения к нулю с положительной стороны «склон» холма (см. рис. 7. 6а) становится всё более пологим, и шарик всё медленнее скатывается в ямку. В точке k = 0 на рисунке имеет место нарушение симметрии в системе, т. е. шарик скатывается в одно из равновесных состояний, причём симметрия нарушается не только в пространстве, но и во времени: шарик скатывается в одно из равновесных состояний необратимо. Нарушение временной симметрии происходит и в системе примера 7: при  С_А < С_А^кр стационарное состояние соответствует нулевой концентрации, и реакция не идёт - это означает полную временную симметрию, а при С_А > С_А^кр стационарное состояние существует при определённой концентрации, и реакция идёт в определенном направлении - симметрия отсутствует. Приведенные примеры 7 и 8 показывают, что нарушение симметрии одной фазы и рождение симметрии другой фазы в точке перехода роднит неравновесные (кинетические) фазовые переходы с равновесными.

 

7. 6. Временная эволюция систем – анализ динамической функции

Проведём изучение устойчивости динамических моделей систем с одной переменной - динамическое уравнение таких систем имеет вид:

                                                              = F(q)                                                 (7. 27)    

Пусть система, описываемая данным уравнением, не градиентная, поэтому при её исследовании будем анализировать характер устойчивости вблизи особых точек. Допустим, что графическое изображение функции F(q) в координатах F-q имеет вид, представленный на рис. 7. 8а. Чтоб определить значения q^(k), отвечающие стационарным состояниям, нужно решить уравнение F(q) = 0 - корнями такого уравнения являются q₀ = q^(k) при k = 1, 2…n:

                

Рис. 7. 8. Графическое изображение системы с одной переменной.

Для анализа устойчивости стационарных состояний дадим системе малое возмущение dq:

                                                q=q₀+ dq® dq= q-q₀.                                   (7. 28)

Разложим F(q) в ряд Тейлора вблизи точки q₀^(k):

                                                (7. 29)

Так как F(q₀) = 0, то в линейном приближении предыдущее уравнение можно переписать в виде:

                                                      ,                                       (7. 30)

где . Решением уравнения будет:

                                                          dq(t)= dq(0) e^pt                                       (7. 31)

Возможны две траектории движения системы вблизи особой точки:

- р < 0, тогда при t ® ¥, то есть стационарное состояние устойчиво;

- p > 0, тогда 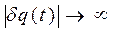 при t ® ¥, то есть стационарное состояние неустойчиво.

Применим полученное решение к анализу ситуации, показанной на рис. 7. 8а. В точке q⁽¹⁾ p < 0 ( вспомним, что р = F^¢ (q₀) - так как наклон кривой в точке отрицателен, то отрицательна и производная), значит, стационарное состояние при q⁽¹⁾ устойчиво. Далее понятно, что поскольку в точке q⁽²⁾ p > 0, то. стационарное состояние при q⁽²⁾ неустойчиво. Сложнее обстоит дело с точкой q⁽³⁾, в которой р = 0 - в этом случае для изучения устойчивости придётся взять второй член разложения функции F(q), при этом получится уравнение:

                                     ,                       (7. 32)

Его решением будет:

                                      .                           (7. 33)       

Если dq(0) < 0, то система со временем возвращается в стационарное состояние при q⁽³⁾, а если dq(0) > 0, то она со временем от него уходит – значит, состояние при q⁽³⁾ неустойчивое.

Теперь, зная всё о стационарных состояниях заданной функции F(q), можно нарисовать фазовый портрет системы в фазовом пространстве, которое в случае одной переменной представляет собой ось q на рис. 7. 8б. Таким образом, можно заключить, что при исследовании стационарных состояний систем с одной переменной возможны следующие случаи:

F¢ (q₀^(k)) < 0 – стационарное состояние устойчиво,

F¢ (q₀^(k)) > 0 – стационарное состояние неустойчиво,

F¢ (q₀^(k)) = 0 –стационарное состояние неустойчиво.

Мы изучали устойчивость только особых точек q₀ - во всех практически важных случаях этого оказывается достаточно, так как нас обычно интересует поведение системы не во всем фазовом пространстве, а в какой-то очень ограниченной его части. Поэтому и в дальнейшем, для большего числа переменных мы сосредоточим внимание только на асимптотической устойчивости состояний.

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: