8. Нелинейная термодинамика –динамические модели процессов с двумя переменными

8. НЕЛИНЕЙНАЯ ТЕРМОДИНАМИКА –ДИНАМИЧЕСКИЕ МОДЕЛИ ПРОЦЕССОВ С ДВУМЯ ПЕРЕМЕННЫМИ

 

8. 1. Точечные конечные состояния, классификация, фазовые портреты, эволюция систем

Запишем уравнение модели для системы с двумя переменными:

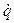                                                      _{1, 2} = F_{1, 2} (q₁, q₂).                                              (8. 1)

Действуя так же, как в предыдущем разделе, определим особые точки, решив стационарные уравнения:

                                                                 F₁(q₁, q₂)=0;                                                              

                                                            F₂(q₁, q₂)=0.                                                (8. 2)       

Отсюда получим стационарные решения q_{1, 2}^(s). Придадим системе возмущения по обоим переменным dq₁ и dq₂ :

                                                                                            

                                                                            (8. 3)      

 

Подставив dq₁, dq₂ в дифференциальные уравнения для F_{1, 2}, разложим функции F_{1, 2} в ряд вблизи исследуемой особой точки q_{1, 2}^(S), тогда в линейном приближении получим:

                                                                                          

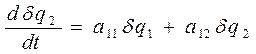
                                    ,                           (8. 4)

причём │ q_{1, 2(s).}

Будем искать решение полученной системы линейных обыкновенных дифференциальных уравнений в известном виде:

                                         ;                                             

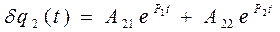                               ,                        (8. 5)       

 

где А_ik - постоянные интегрирования, которые зависят от начальных значений  dq_{1, 2} (0). Для определения р_{1, 2} запишем характеристическое уравнение системы дифференциальных уравнений (8. 4), подставив  (8. 5) в (8. 4):

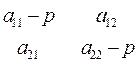                                        = 0                                          (8. 6)

 

Раскрывая определитель, получим:

        .            (8. 7)

Это уравнение является квадратными относительно р, то есть оно имеет два решения р₁ и р₂. Исследуем всевозможные сочетания корней р₁, р₂ - их всего шесть:

· р₁, р₂ - действительные отрицательные числа, тогда возмущения со временем «рассасываются» (показатели экспонент отрицательны); особая точка является устойчивым узлом - траектории вблизи устойчивого узла и зависимость от времени приведены на рис. 8. 1.

Рис. 8. 1. Траектория вблизи устойчивого узла (а) и поведение системы (б).

· р₁, р₂ - действительные положительные числа, при этом возмущения растут неограниченно; особая точка - неустойчивый узел, показанный на рис. 8. 2.

Рис. 8. 2. Траектория вблизи неустойчивого узла (а) и поведение системы (б).

· р₁, р₂ - действительные числа, имеющие разные знаки (одна из экспонент растёт, другая убывает); особая точка – седло, и она неустойчива (рис. 8. 3).

 

Рис. 8. 3. Траектория вблизи седла (а) и поведение системы (б).

· р₁, р₂ - комплексные числа с положительной действительной частью; особая точка - неустойчивый фокус; траектория вблизи особой точки и поведение системы показаны на рис. 8. 4.

     q₁

 

 

                                          

                                                       q₂                                                   t

                         а                                                     б

Рис. 8. 4. Траектория вблизи неустойчивого фокуса (а) и поведение системы (б).

· р₁, р₂ - комплексные числа с отрицательной действительной частью; особая точка - устойчивый фокус - показана на рис. 8. 5.

                                       

                                       

 

 

 

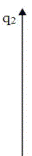
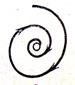
а                                                     б

Рис. 8. 5. Траектория вблизи устойчивого фокуса (а) и поведение системы (б).

· р₁, р₂ - числа чисто мнимые, тогда решение выражается тригонометрическими функциями, показанными на рис. 8. 6; особая точка – центр, который обладает устойчивостью, так как dq_{1, 2} со временем не растут, Поведение системы вблизи центра - типичный пример маргинальной (безразличной) устойчивости.

Рис. 8. 6. Траектория вблизи центра( а) и поведение системы при маргинальной устойчивости (б).

Шести видам фазовых траекторий вблизи особых точек соответствуют шесть типов поведения системы вблизи стационарного состояния. Вспомним, что система с одной переменной имела всего два возможных типа поведения.

Пример. Проанализируем на устойчивость металлургическую систему, уже рассмотренную нами как пример неравновесных переходов - восстановление вюстита оксидом углерода СО в присутствии твёрдого углерода, только теперь выберем такие условия, при которых восстановительная реакция сильно смещена вправо:

                                                         FeO+CO→ Fe+CO₂ ,                                                        

а реакция газификации протекает обратимо:

                                                     .                                                         

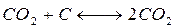Это возможно, например, в том случае, если концентрация (или активная поверхность) твёрдого углерода достаточно велика; кроме того, система открыта, т. е. газы СО и СО₂ могут свободно выходить из реакционной зоны, причём тем быстрее, чем больше их концентрация:

                                                                                                                                     

                                                                                                                                 

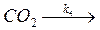
Будем следить за изменением концентраций обоих газов, при этом концентрацию СО обозначим x, СО₂ - y. Тогда кинетические уравнения (модель системы) можно записать в виде:

             

              ,           (8. 8)

где  (k₁ - константа скорости прямой реакции газификации, S_FeO - эффективная реакционная поверхность вюстита);
 (k₂ - константа скорости обратной реакции газификации, S_c - эффективная реакционная поверхность твердого углерода). Для анализа данной системы определим стационарные состояния, решив стационарные уравнения:

                                                  

                                              .                                (8. 9)                                           

Мы обнаружим, что стационарное состояние единственное 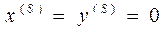. Исследуем поведение системы вблизи стационарного состояния, для чего придадим концентрациям малые возмущения δ х и δ y, подставим их в кинетическое уравнения и отбросим все члены, кроме линейных – тогда получим систему линейных дифференциальных уравнений. Найдём её коэффициенты :

                                                                                          

                                                 ;                                                     

                                                  ;                                                  

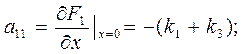
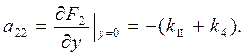                                                      (8. 10)      

 

Далее воспользуемся характеристическим уравнением, подставив в него полученные значения

                                         (8. 11)

где 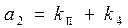. Решение характеристического уравнения таково:

                                    (8. 12)

Полученное решение свидетельствует, что его корни р₁ и р₂ всегда действительны (выражение в квадратных скобках всегда положительно) и меньше нуля р₁ < 0, р₂ < 0 ( так как второй член решения всегда меньше первого) - это значит, что стационарная точка есть устойчивый узел: концентрация СО и СО₂ со временем стремятся к нулю, причём реакция затухает – то есть становится ясно, что реальная восстановительная система, соответствующая данной модели, самопроизвольно функционировать не может. Для стационарного протекания восстановительной реакции схему опыта надо изменить (например, создать постоянный приток монооксида углерода).

Анализ устойчивости особых точек, проведённый для систем с двумя переменными, можно распространить на системы с произвольным количеством переменных (см. Приложение).

 

⇐ Предыдущая11121314151617181920Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: