9. Общие вопросы устойчивости нелинейных систем

9. ОБЩИЕ ВОПРОСЫ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ

Понятие устойчивости, которое мы прежде многократно упоминали, является центральным при исследовании сложных нелинейных систем. Мы называли стационарное состояние устойчивым, если при неизменных внешних условиях система находится в нём неограниченно долго. Зададимся теперь вопросом, по отношению к чему проявляется устойчивость системы? Мы уже говорили, что в реальных условиях существуют случайные неконтролируемые возмущения – флуктуации, и если система находится в устойчивом состоянии, то флуктуации, например, начальных условий не отразятся на дальнейшем поведении системы - она всё равно останется в этом состоянии. И наоборот, флуктуации, как бы они не были малы, помешают системе задержаться в неустойчивом состоянии - на вершине горы. Здесь мы говорим об устойчивости лишь по отношению к флуктуациям. Значит, для проведения исследования на устойчивость системы, находящейся в заданном стационарном или нестационарном состоянии, необходимо математически определить понятие устойчивости. Существует несколько видов устойчивости систем.

9. 1. Устойчивость по траектории

Рассмотрим некоторую траекторию u_j (t) как движение системы в фазовом пространстве. Эта траектория устойчива, если другие траектории, которые в начальный момент времени t = t₀ были рядом с траекторией u_j (t), не удаляются со временем (рис. 9. 1):

Рис. 9. 1. Поведение двух соседних траекторий движения системы в случае устойчивости по траектории.

Поясним это обстоятельство. Каждая траектория – это единственный путь (поведение) системы при заданных начальных условиях. Разные начальные условия дают разные траектории в фазовом пространстве. Если мы говорим, что траектории были рядом в начальный момент времени, то это значит, что мы изучаем поведение системы при близких начальных условиях. Из того, что траектории со временем не расходятся (остаются поблизости друг от друга) следует, что значения характеризующих систему переменных q_i, имеющие небольшое различие при близких начальных условиях, также незначительно отличаются друг от друга и во все последующие моменты времени - с математической точки зрения это означает, что в окрестности S заданнойтраектории u_j (t) в фазовом пространстве все соседние траектории, исходящие из этой окрестности, всегда остаются в этой окрестности. Тогда говорят, что траектория u_j (t) устойчива (см. рис. 9. 1). Если же нельзя найти такую окрестность, которую соседние траектории в любой последующий момент времени не покидали бы, то траектория u_j (t) неустойчива.

Можно сузить это определение. Пусть соседние траектории u_j(t) и v_j(t) обладают следующими свойствами:

                                  при t → ∞ ,                               (9. 1)

то есть соседние траектории асимптотически стремятся друг к другу. Устойчивость, соответствующая данному определению, называется асимптотической устойчивостью по траектории. Если же

                                 ∞ при t → ∞ ,                            (9. 2)

то мы имеем дело с асимптотически неустойчивой траекторией.

9. 2. Орбитальная устойчивость

Рассмотрим теперь траекторию движения системы с точки зрения её геометрической формы. Пусть дана траектория u₁ (t): если для заданного 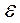 > 0 найдется такое η > 0, чтоточка R, движущаяся по траектории, близкой к u₁ (t) (т. е. по «соседней» траектории в смысле близости начальных условий), в момент t₀ находится от u₁ (t) на расстоянии не более η и при t > t₀ остается на расстоянии не большем 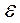, то u₁ (t) – орбитально устойчивая траектория. Это означает, что, если при небольшом изменении переменных q_i системы в начальный момент времени её траектория (орбита) существенно не меняет свою форму в фазовом пространстве, то имеет место орбитальная устойчивость (рис. 9. 2), при этом точки фазового пространства остаются близкими в разные моменты времени:

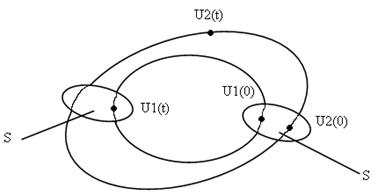
Рис. 9. 2. Движение систем при орбитальной устойчивости (соседние траектории).

Примеры: два самолета, вылетевшие примерно в одно и то же время, но с разными скоростями по одинаковому кольцевому маршруту, пролетают по орбитально устойчивой траектории для данной серии полетов несмотря на то, что расстояние между самолётами в процессе полёта всё время увеличивается. Или пусть имеется движение материальной точки, которое в полярных координатах выражается уравнениями:

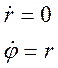                                                                                                                   (9. 3)

Это движения по окружностям такие, что, чем больше радиус окружности r, тем больше угловая скорость 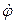  - это значит, две частицы, которые в начале движения были на соседних орбитах с близкими радиусами, со временем расходятся вследствие отличия их угловых скоростей – очевидно, устойчивости по траектории здесь нет, но форма орбиты не меняется при небольших изменениях начального значения r, а следовательно, орбитальная устойчивость здесь имеется.

Орбитальная устойчивость также может быть асимптотической в случае, если расстояние между движущейся по траектории точкой R, первоначально близкой к u₁ (t), и самой траекторией u₁ (t) стремится к нулю при      t → ∞ .

 

⇐ Предыдущая13141516171819202122Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: