9. 3. Структурная устойчивость. 10. Теория катастроф – взгляд со стороны. 10. 1. Катастрофы и анализ структурной устойчивости

9. 3. Структурная устойчивость

Пусть даны уравнения динамической модели системы:

                                                            q_j = F_j,                                                        (9. 4)

где функции F_j часто зависят не только от переменных q_j , но и от внешних параметров , которые называются управляющими параметрами. При фиксированных значениях управляющих параметров поведение системы, описываемое траекториями в фазовом пространстве, однозначно зависит от начальных условий – такая картина, изображающая поле траекторий в интересующей нас области фазового пространства для всех возможных начальных условий, называется фазовым портретом системы. Если при небольших изменениях управляющих параметров структура фазового портрета остаётся без изменений, то говорят, что система обладает структурной устойчивостью («грубая» системв). Наоборот, система является структурно неустойчивой (особенной), если при небольших изменениях хотя бы одного из параметров в фазовом портрете происходят структурные (топологические) изменения. Что это значит? Основные, качественные изменения фазового портрета происходят при изменении характера особых точек или/и циклов, то есть при ветвлении решений - при бифуркациях, которые соответствуют неравновесным фазовым переходам системы. Таким образом, следует отметить, что структурная устойчивость нарушается при неравновесных фазовых переходах, когда состояние системы становится чувствительным к флуктуациям внешних (управляющих) параметров.

10. ТЕОРИЯ КАТАСТРОФ – ВЗГЛЯД СО СТОРОНЫ

10. 1. Катастрофы и анализ структурной устойчивости

Запишем динамическую модель произвольной системы в общем виде

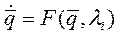                                                    ,                                         (10. 1)

где  - вектор состояния (внутренние параметры), 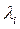 - управляющие (внешние) параметры. Исследуя поведение системы, мы прежде всего определяли стационарные состояния  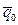и тем или иным способом анализировали, будет ли система оставаться в данном стационарном состоянии или покидает его, т. е. изучали устойчивость стационарных состояний. Кроме того, мы говорили, что при изменении одного или нескольких управляющих параметров прежнее стационарное состояние может терять устойчивость - это означало, что происходит неравновесный переход, то есть система переходит в другую фазу (образование или разрушение диссипативных структур, переход к турбулентности и т. д. ). С точки зрения динамической модели, это означает, что перестраивается фазовый портрет системы, то есть система теряет структурную устойчивость – происходит бифуркация: вспомним, например ангармонический осциллятор или соответствующие химические реакции. Можно рассмотреть и более сложные случаи, когда меняются сразу два или более управляющих параметра - тогда задачу надо исследовать в многомерном пространстве управляющих параметров системы одной переменной (внутреннего параметра), размерность которой равна сумме числа управляющих параметров и переменных (например, при двух параметрах вместо точки бифуркации появляется линия бифуркаций), поэтому задача определения структурной устойчивости в системах, содержащих несколько переменных и управляющих параметров, сильно усложняется и быстро теряет наглядность.

Исследование динамических моделей в пространстве как внутренних, так и внешних параметров является предметом теории катастроф. Катастрофами называются скачкообразные изменения (внезапный ответ системы) при плавном изменении внешних условий, причём ими могут быть как равновесные фазовые превращения, так и неравновесные (динамические) фазовые переходы. В теории катастроф исследуются только градиентные системы, общую модель которых можно схематически представить в виде следующих уравнений:

                                  ,                             (10. 2)

При этом стационарные (равновесные) состояния определяются условием:

                                                          .                                            (10. 3)

Французский математик Р. Тома доказал теорему, согласно которой для общего числа параметров (внутренних и управляющих) k  5 потенциальная функция системы путём гладкой замены переменных может быть приведена к некоторой канонической форме. Разберём два примера исследования нарушений структурной устойчивости в простых системах, потенциал которых уже приведен к канонической форме: