10.2. Катастрофа «складки»

Пример 1. Рассмотрим систему с одним управляющим параметром, потенциал которой можно выразить в форме:

                                           ,                                       (10. 4)

где a – единственный управляющий параметр. Такого типа потенциал мы уже рассматривали для случая нелинейных химических систем. Форма этого потенциала при изменении параметра a качественно меняется, что показано на рис. 10. 1:

Рис. 10. 1. Задача с одним управляющим параметром в теории катастроф - форма потенциала.

Найдём параметры катастрофы, т. е. скачкообразного изменения формы потенциала, и вид сответствующего бифуркационного множества, для чего требуется определить прежде геометрическое место точек стационарного состояния на плоскости параметров q – a: dV/dq = q² + a = 0. Полученное уравнение описывает геометрическое место особых (стационарных) бифуркационных точек (точек, соответствующих решению полученного уравнения): видно, что оно имеет решение только в отрицательной полуплоскости, а в правой (положительной) полуплоскости особых точек нет (см. рис. 10. 2). В точке a = 0 происходит переход от отсутствия решений сразу к двум решениям, которую поэтому называют двукратно-вырожденной. Из вида потенциала (рис. 10. 1) следует, что положение двукратно-вырожденной точки находят решением уравнения d²V/dq² = 0, откуда q = 0 и a = 0. Эта особая двукратно-вырожденная бифуркационная точка и представляет собой искомое бифуркационное множество в пространстве управляющего параметра a (рис. 10. 2б), при этом в системе имеется катастрофа складки, в соответствии с формой стационарных состояний в простанстве одного параметра a:

Рис. 10. 2. Катастрофа типа «складка»: а – геометрическое место особых (стационарных) точек, б – диаграмма решений и точка бифуркации.

10. 3. Катастрофа «сборки »

Пример 2. Рассмотрим задачу с двумя управляющими параметрами, при этом

потенциал системы может быть преведён к виду:

                              ,                           (10. 4)

где a и b – управляющие параметры. Построим стационарную поверхность в пространстве параметров  q – a – b , для чего решим стационарное уравнение:

                                           .                              (10. 5)

Внешний вид поверхности равновесия (стационарности), определяемый этим уравнением, показан на рис. 10. 3:

Рис. 10. 3. Катастрофа типа «сборки» в двухпараметрической задаче: а – поверхность равновесия в пространстве параметров; б – бифуркационное множество (сепаратриса) на плоскости a – b.

Предположим, что в системе присутствует катастрофа - проверим это, определив вид геометрического места двукратно-вырожденных особых точек в прастранстве параметров a – b, для чего решим соответствующее уравнение:

                                  .                   (10. 6)

Подставив полученное значение а в уравнение стационарной (равновесной) поверхности, получим b = 2q². Таким образом, система уравнений

                                                                  a = - 3q²

                                                b = 2q³                                                              (10. 7)

определяет положение бифуркационного множества на плоскости управляющих параметров a – b – в данном случае множество представляет собой линию, которая называется сепаратрисой, состоящую из двух симметрично расположенных ветвей, каждая из которых разделяет на плоскости параметров области с разным типом потенциала. Точка соединения ветвей сепаратрисы носит название трёхкратно-вырожденной особой точки, поскольку её положение определяется уравнением (как видно, она находится в начале координат):

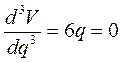                                                    ,                                       (10. 8)

откуда q = 0 и a = b = 0. Катастрофа канонической формы потенциала в данном примере, видимо, также из-за внешнего сходства поверхности равновесия с портновской сборкой носит название катастрофы сборки.

Итак, если система градиентная, то с помощью теории катастроф легко исследовать структурную устойчивость системы - найти точки, линии или поверхности бифуркационного множества, а значит, определить, где (при каких значениях управляющих параметров) расположена граница, разделяющая различные фазы (состояния) системы. Для этого прежде надо привести потенциал системы к каноническому виду и определить все n-кратно-вырожденные особые точки (n = 1, 2…k, где k – общее количество параметров системы).

Итак, что надо сделать, чтобы исследовать в общем случае поведение неравновесной нелинейной системы? Несмотря на многообразие неравновесных процессов и сложность реальных систем, предыдущее рассмотрение показало, что возможен некоторый единый подход, позволяющий в ряде случаев получить интересующие нас данные относительно поведения нелинейных систем - этот подход можно попытаться выразить в виде краткого алгоритма, один из возможных вариантов которого мы приводим ниже:

1. Необходимо построить динамическую модель исследуемой системы, то есть представить динамику системы в виде дифференциальных уравнений по возможности так, чтобы число независимых уравнений было не меньше числа независимых переменных (внутренних параметров).

2. Решая стационарные уравнения, нужно определить особые точки, которые соответствуют стационарным или равновесным состояниям.

3. Если модель описывается градиентной системой уравнений, можно исследовать устойчивость стационарных состояний по форме потенциала или путём линейного анализа устойчивости (можно использовать локальный критерий Гурвица, см. приложение 1); если полное число переменных не более пяти можно, воспользоваться методами теории катастроф, а для неградиентных систем следует использовать глобальный критерий Ляпунова (см. приложение).