Линейная зависимость (независимость) системы векторов.

ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ

РОССИЙСКОЙ ФЕДЕРАЦИИ

БАРНАУЛЬСКИЙ ФИЛИАЛ

 

 

Н.Т. Копылова

 

 

Математика

Конспект лекций

 

для студентов, обучающихся по направлению

38.03.02 «Менеджмент

 

Рассмотрен и одобрен

на заседании кафедры «Математика и информатика»

протокол № 1 от 28 августа 2015 года

 

 

Барнаул – 2015

 

Оглавление

Тема 1. Матрицы и определители. 3

Тема 2. Системы линейных уравнений. 14

Тема 3. Неотрицательные матрицы и модель Леонтьева. 21

Тема 4. Множества и прямое произведение. 25

Тема 5. Теория графов. 30

Тема 6. Теория пределов. 38

Тема 7. Дифференциальное исчисление функций одной переменной. 44

Тема 8. Интегральное исчисление функций одной переменной. 51

Тема 9. Дифференциальное исчисление функций нескольких переменных. 57

Тема 10. Ряды.. 62

Рекомендуемая литература. 68

 

Тема 1. Матрицы и определители

Арифметические векторы и линейные операции над ними

Определение 1. Арифметическим п - мерным вектором называется любая последовательность из п действительных чисел .

Краткая запись . Числа называются координатами вектора. Например, вектор имеет координаты 0, -2, 1, 5.

Геометрически можно изобразить только одномерные (направленные отрезки на прямой), двумерные (на плоскости), трёхмерные (в пространстве) арифметические векторы.

Определение 2. Два вектора и с одним и тем же числом координат , будем считать равными в том и только том случае, когда Равенство векторов обозначается обычным образом .

Определение 3. Суммой двух векторов называется вектор

.

Вектор 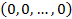называется нулевым и обозначается . Вектор называется противоположным вектору и обозначается .

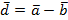
Свойства сложения векторов

1. .

2. .

3. .

4. .

Определение 4. Произведением вектора на число k называется вектор

.

Свойства умножения вектора на число

5. .

6.

7.

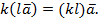
8.

Упражнение. Даны векторы . Найдите вектор

Определение 5. Множество всех п – мерных арифметических векторов, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее восьми свойствам, называется арифметическим п – мерным векторным пространством и обозначается .

Определение 6. Некоторое множество U образует линейное пространство, если для любых его элементов определена операция сложения 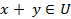и для каждого элемента и любого действительного числа определено произведение причём эти операции удовлетворяют свойствам 1-8 (см. выше).

Линейным пространством является, например, множество всех алгебраических многочленов степени, не превышающей натурального числа п.

 

Линейная зависимость (независимость) системы векторов.

Определение 7. Векторы называются линейно зависимыми, если существуют такие числа , не равные одновременно нулю, что

. (1)

Если равенство выполняется только при , то векторы называются линейно независимыми.

Пример. Система векторов линейно зависима, так как .

Определение 8. Векторы называются коллинеарными, если они параллельны одной прямой, т.е. или .

Утверждение. Система, содержащая два вектора , линейно зависима в том и только том случае, когда эти векторы коллинеарны.

Определение 9. Три вектора в R³, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными.

 

Определение 10. Линейное пространство R^п называется п - мерным, если в нём существует п линейно независимых векторов, а любые из (п + 1) векторов уже являются зависимыми. Размерность пространства – это максимальное число содержащихся в нём линейно независимых векторов. Число п называется размерностью пространства R^п и обозначают dim (R^п).

Определение 11. Система векторов из R^п называется базисом пространства в R^п, если:

1. эти векторы линейно независимы;

2. любой вектор из R^п является линейной комбинацией векторов данной системой.

Следовательно, базисом на плоскости будут любые два неколлинеарных вектора, а в пространстве – любые три некомпланарных вектора.

Теорема. Линейно независимая система векторов в R^п тогда и только тогда является базисом, когда их число равно п.

Теорема. Каждый вектор линейного пространства R можно представить (и при том единственным способом) в виде линейной комбинации векторов базиса.

Определение 12. Вектор единичной длины называется нормированным. Если , то вектор нормирован.

Примером базиса в R^п может служить лестничная система векторов

Если вектор произвольный вектор из R^п, то очевидное равенство

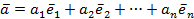
показывает, что есть линейная комбинация векторов .

 

 

12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: