 |
Тема 9. Дифференциальное исчисление функций нескольких переменных
|
|
|
|
Определение. Частным приращением функции 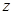 по переменной
по переменной 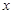 называется выражение
называется выражение 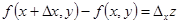 .
.
Аналогично определяется частное приращение функции 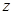 по переменной
по переменной  :
:
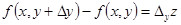 .
.
Определение. Частной производной функции двух переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при стремлении последнего к нулю (если этот предел существует).
Пусть 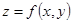 , тогда
, тогда
 ,
,
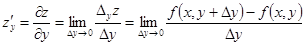 .
.
Определение. Пусть функция 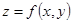 имеет частные производные
имеет частные производные 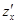 и
и 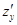 , которые также являются функциями двух переменных
, которые также являются функциями двух переменных 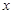 и
и  . Частные производные от этих функций называются частными производными второго порядка от функции
. Частные производные от этих функций называются частными производными второго порядка от функции 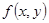 . Каждая производная первого порядка имеет две частные производные. Таким образом, мы получаем 4 частные производные второго порядка, которые обозначаются следующим образом:
. Каждая производная первого порядка имеет две частные производные. Таким образом, мы получаем 4 частные производные второго порядка, которые обозначаются следующим образом:
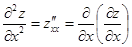 , ,
| 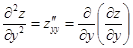 , ,
|
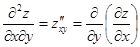 , ,
| 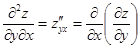 . .
|
Определение.  и
и  называются смешанными производными функции
называются смешанными производными функции 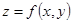 .
.
Пример. Найти частные производные первого порядка функции 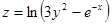 .
.
Решение. Частная производная функции двух переменных 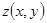 по переменной х обозначается
по переменной х обозначается 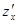 или
или 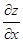 и вычисляется по правилам и формулам дифференцирования функции одной переменной при условии, что х – изменяется, а у – постоянная (const).
и вычисляется по правилам и формулам дифференцирования функции одной переменной при условии, что х – изменяется, а у – постоянная (const).

Слагаемое 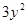 не зависит от переменной х, следовательно, по правилу
не зависит от переменной х, следовательно, по правилу  производная
производная
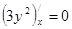 . Функция
. Функция 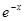 зависит от переменной х, применим для ее дифференцирования формулу
зависит от переменной х, применим для ее дифференцирования формулу 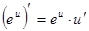 .
.
 .
.
Частная производная функции 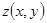 по переменной у обозначается
по переменной у обозначается 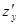 или
или  и вычисляется при условии, что у – изменяется, а х – const.
и вычисляется при условии, что у – изменяется, а х – const.


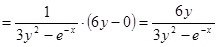 .
.
Определение. Точка  называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции 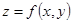 , если существует окрестность точки
, если существует окрестность точки 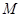 такая, что для всех точек
такая, что для всех точек  этой окрестности выполняется неравенство
этой окрестности выполняется неравенство
|
|
|
 ,
,
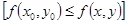 .
.
Теорема (необходимое условие экстремума). Пусть точка 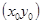 - есть точка экстремума дифференцируемой функции
- есть точка экстремума дифференцируемой функции 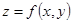 . Тогда частные производные
. Тогда частные производные 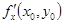 и
и 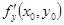 в этой точке равны нулю.
в этой точке равны нулю.
Теорема (достаточное условие экстремума). Пусть функция  :
:
а) определена в некоторой окрестности критической точки 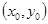 , в которой
, в которой
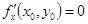 и
и 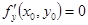 ,
,
б) имеет в этой точке непрерывные частные производные второго порядка
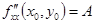 ,
,
 ,
,
 .
.
Тогда, если  , то в точке
, то в точке 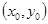 функция
функция 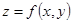 имеет экстремум, причем если
имеет экстремум, причем если 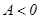 (или
(или 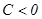 ) – максимум, если
) – максимум, если 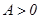 (или
(или 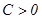 ) - минимум. В противном случае функция экстремума не имеет.
) - минимум. В противном случае функция экстремума не имеет.
Если 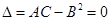 , то вопрос о наличии экстремума остается открытым.
, то вопрос о наличии экстремума остается открытым.
Пример. Исследовать на экстремум функцию  .
.
Решение. Найдем частные производные 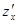 и
и 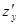 :
:
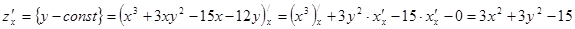 ;
;
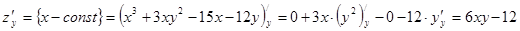 .
.
Запишем необходимые условия экстремума функции 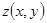 :
:

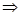
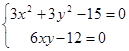
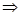
 .
.
Решим полученную систему уравнений. Для этого выразим из второго уравнения 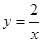 ,
, 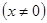 и подставим в первое
и подставим в первое  , упростим
, упростим 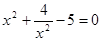
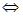
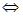
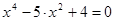 .
.
Обозначим 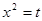 и решим полученное квадратное уравнение
и решим полученное квадратное уравнение 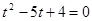 . Дискриминант
. Дискриминант 
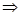
 ,
, 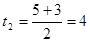 .
.
Из условия 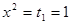 найдем
найдем 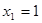 ,
, 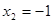 .
.
Из условия  найдем
найдем  ,
,  .
.
В соответствии с формулой 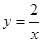 определим
определим 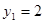 ,
,  ,
, 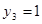 ,
, 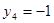 .
.
Таким образом, критическими точками заданной функции будут
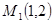 ,
, 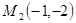 ,
, 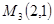 и
и  .
.
Для проверки достаточного условия экстремума найдем частные производные второго порядка: 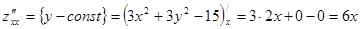 ;
;
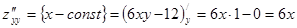 ;
;
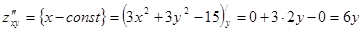 .
.
В каждой критической точке М вычислим значения этих производных 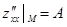 ,
, 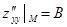 ,
,  и найдем определитель
и найдем определитель 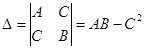 .
.
В точке 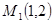 :
:  , следовательно, точка
, следовательно, точка 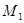 не является точкой экстремума функции
не является точкой экстремума функции 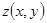 .
.
В точке 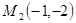 :
: 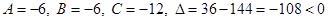 , следовательно, точка
, следовательно, точка 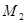 не является точкой экстремума функции
не является точкой экстремума функции 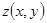 .
.
В точке 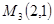 :
: 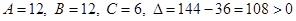 , следовательно, точка
, следовательно, точка 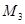 является точкой экстремума функции
является точкой экстремума функции 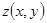 . При этом
. При этом 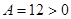 , значит, в точке
, значит, в точке 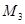 функция имеет минимум,
функция имеет минимум,  .
.
В точке  :
:  , следовательно, точка
, следовательно, точка  является точкой экстремума функции
является точкой экстремума функции 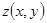 . При этом
. При этом 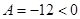 , значит, в точке
, значит, в точке  функция имеет максимум, значение которого составляет
функция имеет максимум, значение которого составляет
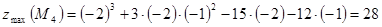 .
.
Пример. Имеются данные о затратах на обслуживание У (тыс. руб.) и сроке эксплуатации Х (лет) некоторого оборудования.
| Х | ||||
| У |
|
|
|
Пользуясь методом наименьших квадратов аппроксимировать данные линейной зависимостью  и определить с ее помощью приближенное значение затрат при сроке эксплуатации
и определить с ее помощью приближенное значение затрат при сроке эксплуатации 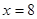 лет. Вычислить сумму квадратов отклонений найденной прямой от исходных точек. (Расчет коэффициентов a и b выполнить с точностью 2 знака после запятой.)
лет. Вычислить сумму квадратов отклонений найденной прямой от исходных точек. (Расчет коэффициентов a и b выполнить с точностью 2 знака после запятой.)
Решение.
Для определения коэффициентов линейной зависимости составим систему нормальных уравнений:
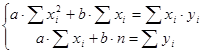 .
.
Вычисление необходимых сумм проведем в таблице:

| 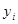
| 
| 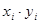
| |
| сумма |
Запишем систему 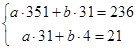 и решим ее по формулам Крамера.
и решим ее по формулам Крамера.
 , система имеет единственное решение.
, система имеет единственное решение.
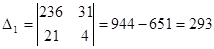
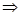
 ;
;
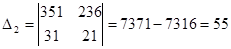
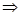
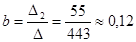 .
.
Таким образом, требуемая линейная зависимость построена: 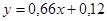 .
.
Определим с ее помощью приближенное значение затрат у при сроке эксплуатации 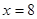 лет:
лет:  (тыс. руб.).
(тыс. руб.).
Для вычисления суммы квадратов отклонений найденной прямой от исходных точек дополним расчетную таблицу столбцами 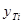 ,
,  и
и 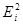 . Теоретические значения
. Теоретические значения 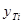 найдем с помощью полученной формулы
найдем с помощью полученной формулы 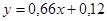 для каждого заданного значения
для каждого заданного значения  . Отклонения
. Отклонения  рассчитаем по формуле
рассчитаем по формуле 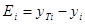 . Затем определим квадраты отклонений и их сумму.
. Затем определим квадраты отклонений и их сумму.

| 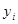
| 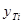
| 
| 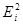
| |
| 0,78 | -0,22 | 0,0484 | |||
| 3,42 | 0,42 | 0,1764 | |||
| 6,72 | -0,28 | 0,0784 | |||
| 10,02 | 0,02 | 0,0004 | |||
| сумма | 0,3036 |
Сумма квадратов отклонений найденной прямой от исходных точек найдена:  .
.
Тема 10. Ряды
Числовые ряды
Определение. Числовым рядом называется бесконечная последовательность чисел  соединенных знаком сложения:
соединенных знаком сложения:
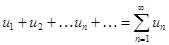 , (10.1)
, (10.1)
где 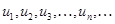 называются членами ряда,
называются членами ряда,
а 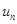 - общим или
- общим или  -м членом ряда,
-м членом ряда,  - натуральные числа.
- натуральные числа.
Определение. Сумма первых  членов ряда
членов ряда 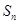 называется
называется  -й частичной суммой ряда.
-й частичной суммой ряда.
Определение. Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е.
 . (10.2)
. (10.2)
Число 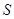 называется суммой ряда, поэтому можно записать
называется суммой ряда, поэтому можно записать
 . (10.3)
. (10.3)
Определение. Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.
|
|
|


