 |
Различные критерии продуктивности модели Леонтьева
|
|
|
|
Определение. Матрица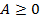 
называется продуктивной, если для любого вектора 
существует решение 
уравнения (3.4).
В этом случае и модель Леонтьева, определяемая матрицей А, тоже называется продуктивной. Другими словами, модель продуктивна, если любое коечное потребление 
можно обеспечить при подходящем выловом выпуске 
.
Уравнение (3.4) можно переписать в виде
.
Если обратная матрица 
существует, то отсюда следует
.
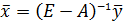Первый критерий продуктивности. Матрица 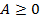продуктивна тогда и только тогда, когда матрица существует и неотрицательна.
Второй критерий продуктивности. Неотрицательная квадратная матрица А продуктивна тогда и только тогда, когда её число Фробениуса меньше единицы.
Пример. Показать продуктивность матрицы
Решение. Сумма элементов каждого столбца меньше единицы. Согласно теореме 2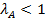 
. Значит, А – продуктивна.
Третий критерий продуктивности. Неотрицательная матрица А продуктивна тогда и только тогда, когда сходится бесконечный ряд
Лемма. Если бесконечный ряд (из матриц) сходится, то его сумма есть матрица .
Тема 4. Множества и прямое произведение
Понятие множества принадлежит к числу первичных неопределяемых понятий математики. Можно сказать, что множество – это любая определённая совокупность объектов. Объекты, из которых составлено множество, называются его элементами. Элементы множества различны и отличимы друг от друга.
Пример. Множество страниц в конспекте. Множество натуральных чисел N.
Если объект х является элементом множества М, говорят, что х принадлежит М. Обозначение: 
. В противном случае говорят, что х не принадлежит М. Обозначение: 
.
Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать различными способами:
|
|
|
Перечислением элементов: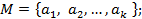 
Характеристическим свойством (предикатом): 
Порождающей процедурой): 
.
Множество, не содержащее элементов, называется пустым. Обозначение: 
.
Обычно в конкретных рассуждениях элементы всех множеств берутся из некоторого одного, достаточно широкого множества U (своего для каждого случая), которое называется универсальным множеством (или универсумом).
Определение. Характеристической функцией множества А называется функция принадлежности элементов U множеству А
Множества совпадают тогда и только тогда, когда совпадают их характеристические функции.
Множество А содержится в множестве В (множество В включает множество А), если каждый элемент А есть элемент В
.
В этом случае А называют подмножеством В. Если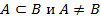 
, то А называется собственным подмножеством В. Иначе – несобственным 
.
Например, множество натуральных чисел N является подмножеством множества целых чисел Z, а последнее в свою очередь является подмножеством множества рациональных чисел Q, то есть N ⊂ Z и Z ⊂ Q, или, короче, N ⊂ Z ⊂ Q.
Для заданного множества A обозначим через 2 A множество всех его подмножеств.
Пример. Пусть A ={ a, b, c }. Тогда множество 2 A состоит из следующих элементов:
{∅}, { a }, { b }, { c }, { a, b }, { a, c }, { b, c }, { a, b, c }.
Далее будет показано, что если множество A конечно и содержит n элементов, то это множество имеет 2 n подмножеств, то есть |2 A |=2| A |.
Два подмножества равны, если они являются подмножествами друг друга.
Мощность множества М обозначается как 
Для конечных множеств мощность – это число элементов. Если 
, то множества А и В называются равномощными (эквивалентными).
Множество называется счётным, если оно эквивалентно множеству натуральных чисел N.
Схема свёртывания
В общем случае множество можно определять по так называемой схеме свёртывания.
|
|
|
При заданном характеристическом свойстве F и заданном классе элементов K множество A определяется как множество, которое содержит все элементы из K, обладающие свойством F. Для определения по схеме свертывания используется следующая запись:
A = { x | x обладает свойством F }.
Применяя сокращение F (x) для обозначения того, что элемент x обладает свойством F, будем писать A = { x | F (x)}.
Класс K может быть указан явно; в этом случае используется запись
A = { x ∈ K | F (x)}.
Множество четных чисел P можно определить как
P = { x | x – четное целое число},
или как
P = { x ∈ Z | x четно},
где через Z обозначено множество целых чисел.
Парадокс Рассела
Рассмотрим множество всех множеств, не содержащих себя в качестве элемента:
.
Если множество 
существует, то мы должны иметь возможность ответить на следующий вопрос: 
Пусть 
, тогда 
. Пусть , тогда . Получается неустранимое логическое противоречие, которое известно как парадокс Рассела.
Операции над множествами
1.Объединение
= 
.
2.Пересечение
= 
.
3.Разность
= 
.
4.Симметрическая разность
.
.
.
5.Дополнение
Диаграммы Эйлера-Венна
Законы алгебры множеств
Пусть задан универсум U. Тогда для любых множеств 
выполняются следующие свойства.
1. Идемпотентность:
2. Коммутативность:
3. Ассоциативность:
4. Дистрибутивность:
5. Поглощение:
6. Свойства нуля:
7. Свойства единицы:
8. Инволютивность:
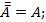
9. Законы де Моргана:
10. Свойства дополнения:
11. Выражение для разности:
.
Убедиться в справедливости перечисленных свойств можно путем несложной непосредственной проверки.
Пример. Проверим первый из законов де Моргана. Покажем сначала, что 
. Предположим, что 
. Тогда x ∉ A ∩ B, так что x не принадлежит хотя бы одному из множеств A и B. Таким образом, x ∉ A или x ∉ B, то есть 
или 
. Это означает, что 
. Мы показали, что произвольный элемент множества 
является элементом множества 
. Следовательно, 
Обратное включение 
доказывается аналогично. Достаточно повторить все шаги предыдущего рассуждения в обратном порядке.
|
|
|
