 |
Формула включений-выключений
|
|
|
|
Теорема. Для любых конечных множеств А и В справедливо равенство

Доказательство. Обозначим  . Тогда
. Тогда

Теорема. Пусть  есть подмножество некоторого конечного множества А. Тогда
есть подмножество некоторого конечного множества А. Тогда

Теорема. Пусть  есть подмножество некоторого конечного множества А. Тогда
есть подмножество некоторого конечного множества А. Тогда


Задача (управдом).
Юрий провёл социальный опрос жителей своего подъезда и выяснил, что 25 из них играют в шахматы, 30 были в Архангельске, 28 летали на самолете. Среди летавших на самолете 18 играют в шахматы и 17 были в Архангельске. 16 жителей играют в шахматы и были в Архангельске, среди них 15 еще и летали на самолете. От управдома Юрий узнал, что всего в подъезде живет 45 человек. Не врет ли управдом?
Решение
Управдом врет. Формула включений и исключений для людей, которые не были в Архангельске, не играют в шахматы, и не летали на самолете дает
45-25-30-28+16+18+17-15= - 2 <0.
Ответ: Управдом врет.
Кортежи и прямое произведение множеств
Определение. Пусть даны множества  Кортежем длины n, составленным из элементов этих множеств, называется конечная последовательность
Кортежем длины n, составленным из элементов этих множеств, называется конечная последовательность  где для всех
где для всех  имеем
имеем 
Элемент  называется k- ой координатой или k- й компонента кортежа.
называется k- ой координатой или k- й компонента кортежа.
Два кортежа равны в том и только случае, когда они имеют одинаковую длину, причём их координаты, стоящие на местах с одинаковыми номерами, равны, т.е. кортежи  и
и  равны только в том случае, когда
равны только в том случае, когда  , причём
, причём  для всех
для всех  .
.
Определение. Прямым (декартовым) произведением множеств 

называется множество всех упорядоченных наборов  где
где 

Рис. Геометрическая интерпретация декартового произведения С = А 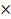 В.
В.
Тема 5. Теория графов
Основные понятия теории графов
Графом G (V, E) называется конечное непустое множество вершин V и конечное множество ребер E. Каждое ребро связывает пару вершин. Если ребро e соединяет вершины v1 и v2, то говорят, что ребро e и вершины v1 и v2 инцидентны.
|
|
|
Два ребра, связывающие одну и ту же пару вершин v1 и v2, называются кратными. Ребро, связывающее вершину саму с собой, называется петлей. Степенью вершины графа называется число ребер графа, инцидентных этой вершине (петли считаются дважды). Степень вершины v обозначается d (v). Вершина степени 0 называется изолированной, вершина степени 1 – висячей. Вершина графа называется четной, если ее степень четна, и нечетной, если нечетна.
Поскольку ребро, соединяющее вершины v1 и v2, добавляет по единице в степени ребер d (v1) и d (v2), справедливо соотношение:
 ,
,
где m – количество ребер графа.
Граф называется полным, если каждые две различные его вершины соединены одним и только одним ребром.
Матрицей смежности графа G (V, E) называется квадратная матрица А (G) n- го порядка (n – число вершин) с элементами:

Если в графе нет петель, то на главной диагонали матрицы смежности стоят нули. Если же в графе нет кратных ребер, то все элементы матрицы равны либо нулю, либо единице.
Матрицей инцидентности графа G (V, E) называется матрица В (G) размера n x m (n – число вершин, m – число ребер) с элементами:

Пример 1. Для графа, изображенного на рис. 1, построить матрицы смежности и инцидентности.
Р е ш е н и е. Начнем с построения матрицы смежности А (G).У данного графа пять вершин, следовательно, матрица смежности будет иметь размер 5 х 5. Поскольку у графа есть петля и она находится в первой вершине, то на главной диагонали элемент матрицы  = 1,а все остальные
= 1,а все остальные  = 0.
= 0.
Ребро  соединяет первую и вторую вершины. Других ребер, соединяющих эти же вершины нет, следовательно,
соединяет первую и вторую вершины. Других ребер, соединяющих эти же вершины нет, следовательно,  . Аналогично,
. Аналогично, 
Рёбра  и
и  соединяют четвёртую и пятую вершины и являются кратными, поэтому
соединяют четвёртую и пятую вершины и являются кратными, поэтому  . Все остальные
. Все остальные  равны нулю.
равны нулю.
Таким образом, матрица смежности имеет вид:
|
|
|
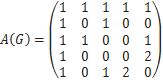
 |




 1 3
1 3



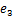




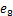



 4
4
 5
5
Рис.1.
Теперь построим матрицу инцидентности В (G). Так как у графа пять вершин и девять ребер, матрица В (G) есть матрица размера 5x 9.
Первое ребро – это петля в первой вершине, поэтому в первом столбце, который соответствует первому ребру, только один элемент b 11 = 1, а все остальные равны нулю.
Второе ребро соединяет первую и вторую вершины, следовательно, b12 = b22 = 1, а все остальные элементы второго столбца равны нулю.
Рассуждая аналогично, получаем матрицу инцидентности:
 .
.
Ориентированные графы
Направленные ребра графа, т.е. ребра, для которых определены вершины, из которых они выходят, и вершины, в которые они входят, называются дугами. Если все ребра графа направлены, то он называется ориентированным графом, или орграфом.
Матрицей смежности ориентированного графа G (V, E) называется квадратная матрица А (G) n- го порядка (n – число вершин) с элементами:

Матрицей инцидентности ориентированного графа G (V, E) называется матрица В (G) размера n x m (n – число вершин, m – число ребер) с элементами:

Пример 2. Построить орграфы по матрицам смежности и инцидентности:
 ,
,

| -1 | |||||||
| -1 | -1 | ||||||
| -1 | -1 | ||||||
| -1 | -1 | ||||||
| -1 |
Р е ш е н и е. 1. Данная матрица смежности – квадратная матрица пятого порядка, следовательно, у рассматриваемого графа пять вершин. Первая и четвертая строки смежной матрицы нулевые, т.е. из первой и четвертой вершин не выходит ни одной дуги. Во второй строке два элемента отличны от нуля, причем a 21 = 2, a 25 = 1, следовательно, из второй вершины выходят три дуги: две в первую вершину и одна в пятую (рисунок 2).




















 1 2 2 e5 3
1 2 2 e5 3
e1 e2



 e6 1 e3 e7
e6 1 e3 e7










 5 3 e4
5 3 e4
 |

 4 5 e8 4
4 5 e8 4
 |
Рисунок 2 Рисунок 3
В третьей и пятой строках по три единицы: a 32 = a 34 = a 35 = 1и a 51= a 53 = a 54 = 1, т.е. из третьей и пятой вершин выходят по три дуги: из третьей – во вторую, четвертую и пятую вершины, а из пятой – в первую, третью и четвертую.
2. Матрица инцидентности имеет размерность 5 х 8, т.е. у искомого графа пять вершин и восемь дуг. В первом столбце a 11 = 1, a 21 = –1, следовательно, первое ребро выходит из первой вершины и входит во вторую. Второе ребро выходит из первой вершины и входит в третью и т.д. Искомый граф представлен на рисунке 3.
|
|
|
Операции над графами
Граф G1 (V 1, E 1), вершины и ребра которого являются вершинами и ребрами графа G (V, E), т.е. V 1  V, E 1
V, E 1  E, называется подграфом графа G. Граф называется полным, если каждые две различные вершины соединены одним и только одним ребром. Подграф G2 (V 2, E 2), графа G (V, E), являющийся полным графом, называется кликой. Максимальная клика – это клика с максимально возможным числом вершин среди всех существующих клик графа.
E, называется подграфом графа G. Граф называется полным, если каждые две различные вершины соединены одним и только одним ребром. Подграф G2 (V 2, E 2), графа G (V, E), являющийся полным графом, называется кликой. Максимальная клика – это клика с максимально возможным числом вершин среди всех существующих клик графа.
У графа, изображенного на рис. 1, существует несколько клик, например, G1 (V1, E1), где V1 ={1; 2; 3}, E1 ={ e 2; e 3; e 6), или G2 (V2, E2, где V2 ={1; 4; 5}, E2 ={ e 4; e5; e 8). Однако клики с четырьмя вершинами в этом графе нет, поскольку для ее существования необходимо, чтобы было четыре вершины со степенью три (без учета кратных ребер), а в данном графе таких вершин только три: первая, третья и четвертая.
Дополнением графа G (V, E) называется граф  , множество вершин которого совпадает с множеством вершин исходного графа, а множество ребер является дополнением множества E, т.е.
, множество вершин которого совпадает с множеством вершин исходного графа, а множество ребер является дополнением множества E, т.е.  .
.
Объединением графов, G1 (V1, E1) и G2 (V2, E2), таких, что  и
и  , называется граф
, называется граф  , множеством вершин которого является множество
, множеством вершин которого является множество  , а множеством ребер – множество
, а множеством ребер – множество  .
.
Пересечением графов G1 (V1, E1) и G2 (V2, E2), называется граф  ,множеством вершин которого является множество
,множеством вершин которого является множество  , а множеством ребер – множество
, а множеством ребер – множество  .
.
Маршруты, цепи и циклы
Маршрутом в графе называется чередующаяся последовательность вершин и ребер  , в которой два любых соседних элемента инцидентны. Если
, в которой два любых соседних элемента инцидентны. Если  , то маршрут называется замкнутым, а если
, то маршрут называется замкнутым, а если  , то открытым.
, то открытым.
Длиной маршрута считается число ребер, которые он содержит. Маршрут называется цепью, если каждое ребро встречается в нем не более одного раза. Цепь, в которой все вершины различны, называется простой цепью. Замкнутая цепь называется циклом, а простая замкнутая цепь – простым циклом. Если есть цепь, соединяющая две вершины  и
и  , то есть и простая цепь, соединяющая эти вершины. Две вершины называются связными, если существует связывающая их простая сеть; в противном случае вершины называются несвязными. Граф называется связным, если каждые две его вершины связные; в противном случае – несвязным.
, то есть и простая цепь, соединяющая эти вершины. Две вершины называются связными, если существует связывающая их простая сеть; в противном случае вершины называются несвязными. Граф называется связным, если каждые две его вершины связные; в противном случае – несвязным.
|
|
|
Деревья и их свойства
Неориентированный граф называется деревом, если он является связным и не имеет циклов. Основные свойства деревьев:
• любые две вершины дерева можно соединить ровно одной простой цепью;
• если дерево G содержит хотя бы одно ребро, то на нем найдется висячая вершина;
• число ребер дерева G на единицу меньше числа его вершин.
Справедливо и обратное утверждение: если у связного графа число ребер на единицу меньше числа вершин, то такой граф является деревом.
Дерево T (V, E1), множество вершин которого совпадает с множеством вершин графа G (V, E), а ребра являются ребрами графа G (E1  E), называется остовным (покрывающим) деревом графа G. Иными словами, остовное дерево графа G – это его подграф, содержащий все вершины и являющийся деревом. Если n – число вершин, а m – число ребер графа G, то любое его остовное дерево имеет n вершин и (n – 1) ребер. Таким образом, остовное дерево получается отбрасыванием (m – n + 1) ребер графа G. Число γ = m – n + 1 называется цикломатическим числом графа G.
E), называется остовным (покрывающим) деревом графа G. Иными словами, остовное дерево графа G – это его подграф, содержащий все вершины и являющийся деревом. Если n – число вершин, а m – число ребер графа G, то любое его остовное дерево имеет n вершин и (n – 1) ребер. Таким образом, остовное дерево получается отбрасыванием (m – n + 1) ребер графа G. Число γ = m – n + 1 называется цикломатическим числом графа G.
Если каждому ребру графа приписано некоторое положительное число, называемое его весом, или стоимостью, то граф называется нагруженным. Стоимостью нагруженного графа считается суммарная стоимость всех его ребер. Многие задачи, связанные с построением экономичных систем сообщения или информационных систем, приводят к задаче поиска остовного дерева минимальной стоимости.
|
|
|


