 |
Тема 7. Дифференциальное исчисление функций одной переменной
|
|
|
|
7.1. Производная функции
Определение. Производной функции  называется предел отношения приращения функции
называется предел отношения приращения функции  к приращению аргумента (независимой переменной)
к приращению аргумента (независимой переменной) 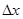 при стремлении последнего к нулю (если этот предел существует):
при стремлении последнего к нулю (если этот предел существует):
 .
.
Обозначают:  .
.
Уравнение касательной к кривой  в точке
в точке 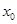 примет вид:
примет вид:
 .
.
Правила дифференцирования. Производные элементарных функций
1. Производная постоянной равна нулю, т.е.  .
.
2. Производная аргумента равна 1, т.е.  .
.
3. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, т.е.
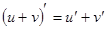 .
.
4. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е.
 .
.
Следствие 1. Постоянный множитель можно вынести за знак производной
 .
.
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений каждого из сомножителей на все остальные:
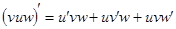 .
.
5. Производная частного двух дифференцируемых функций может быть найдена по формуле:
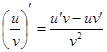 при
при  .
.
Производные элементарных функций
1)  ,
, 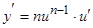 .
.
2)  ,
, 

 .
.
3)  ,
, 

 .
.
4) 
 .
.
5) 
 .
.
6) 
 .
.
7)  ,
, 
Пример. Найти производную функции  .
.
Решение.
Первой применим формулу  . Получим
. Получим
 =
= 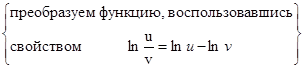 =
=
 {по формулам
{по формулам  и
и 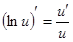 }=
}=

{ применим формулы 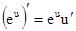 и
и  }
} 
={преобразуем выражение} 
7.2. Приложения производной
Правило Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.
Итак, если имеется неопределенность вида  или
или 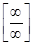 , то
, то
|
|
|
 .
.
Пример. Вычислить предел  .
.
Решение. При  множитель
множитель  является бесконечно большой функцией, а множитель
является бесконечно большой функцией, а множитель  - бесконечно малой. Таким образом, имеем нестандартную неопределенность «
- бесконечно малой. Таким образом, имеем нестандартную неопределенность « ».
».
 = «
= « » =
» =
Преобразуем эту нестандартную неопределенность к стандартному виду (виду дроби):
=  = «
= « » =
» =
Для раскрытия полученной стандартной неопределенности « » используем правило Лопиталя.
» используем правило Лопиталя.
=  =
=  = «
= « » =
» =
Используем правило Лопиталя во второй раз:
=  =
=  = «
= « » = 0.
» = 0.
Пример. Найти уравнение касательной к кривой 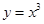 в точке
в точке  . Написать уравнение прямой, проходящей через точку
. Написать уравнение прямой, проходящей через точку  параллельно к этой касательной.
параллельно к этой касательной.
Решение. Уравнение касательной к графику функции  имеет вид
имеет вид  , где
, где  - координаты точки касания,
- координаты точки касания,  - угловой коэффициент касательной.
- угловой коэффициент касательной.
Найдем координаты точки касания: по условию  , тогда
, тогда 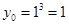 .
.
Найдем угловой коэффициент прямой:  ,
, 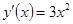 ,
,  .
.
Запишем уравнение касательной  или
или 
Искомая прямая проходит параллельно найденной касательной, следовательно, их угловые коэффициенты связаны соотношением  . Воспользуемся уравнением прямой с угловым коэффициентом, проходящей через точку
. Воспользуемся уравнением прямой с угловым коэффициентом, проходящей через точку  :
:  . Уравнение искомой прямой имеет вид
. Уравнение искомой прямой имеет вид  или
или  .
.
Таким образом, уравнение касательной  ; уравнение искомой прямой
; уравнение искомой прямой  .
.
Теорема (достаточное условие возрастания функции). Если производная дифференцируемой функции положительна внутри некоторого промежутка  , то она возрастает на этом промежутке.
, то она возрастает на этом промежутке.
Теорема (достаточное условие убывания функции). Если производная дифференцируемой функции отрицательна внутри некоторого промежутка  , то она убывает на этом промежутке.
, то она убывает на этом промежутке.
Необходимое условие экстремума. Для того, чтобы функция  имела экстремум в точке
имела экстремум в точке 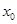 , необходимо, чтобы ее производная в этой точке равнялась нулю (
, необходимо, чтобы ее производная в этой точке равнялась нулю ( ) или не существовала.
) или не существовала.
Замечание. Это условие не является достаточным, т.е. производная в точке 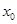 может обращаться в нуль или не существовать, а функция не будет иметь экстремум в этой точке.
может обращаться в нуль или не существовать, а функция не будет иметь экстремум в этой точке.
|
|
|
Теорема (первое достаточное условие экстремума). Если при переходе через точку 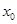 производная дифференцируемой функции
производная дифференцируемой функции  меняет свой знак с плюса на минус, то точка
меняет свой знак с плюса на минус, то точка 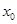 есть точка максимума функции, а если с минуса на плюс, то точка минимума.
есть точка максимума функции, а если с минуса на плюс, то точка минимума.
Теорема (второе достаточное условие экстремума). Если первая производная 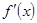 дважды дифференцируемой функции равна нулю в некоторой точке
дважды дифференцируемой функции равна нулю в некоторой точке 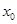 , а вторая производная в этой точке
, а вторая производная в этой точке  положительна, то
положительна, то 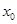 есть точка минимума функции
есть точка минимума функции  , если же
, если же  отрицательна, то
отрицательна, то 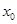 - точка максимума.
- точка максимума.
Пример. Исследовать на экстремум функцию  и найти интервалы монотонности.
и найти интервалы монотонности.
Решение.
1˚. Область определения функции  . Производная функции
. Производная функции  .
.
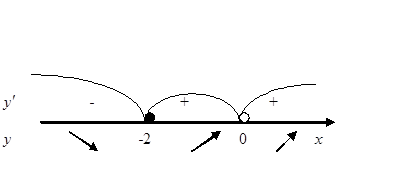 2˚. Приравнивая производную к нулю, находим критическую точку функции
2˚. Приравнивая производную к нулю, находим критическую точку функции  . Точка
. Точка  , в которой производная не существует, является точкой разрыва функции.
, в которой производная не существует, является точкой разрыва функции.
3˚. Покажем критическую точку и область определения функции на числовой прямой. Для определения знака производной в полученных интервалах выберем, например,  и найдем
и найдем
 ,
,  .
.
Следовательно, при всех  функция убывает, а на интервалах
функция убывает, а на интервалах  и
и  функция возрастает. Согласно достаточному условию
функция возрастает. Согласно достаточному условию  – точка минимума данной функции.
– точка минимума данной функции.
4˚. Находим 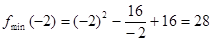 .
.
Пример. Найти асимптоты графика функции  .
.
Решение.
1˚. Область определения  . Найдем пределы функции при
. Найдем пределы функции при  .
.
 , отсюда следует, что прямая
, отсюда следует, что прямая  является вертикальной асимптотой.
является вертикальной асимптотой.
2˚. Исследуем поведение функции на бесконечности:
 .
.
Следовательно, прямая  является горизонтальной асимптотой.
является горизонтальной асимптотой.
3˚. Найдем наклонную асимптоту: 
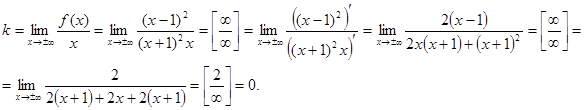 . Таким образом, наклонных асимптот не существует.
. Таким образом, наклонных асимптот не существует.
Пример. Провести полное исследование функции  и построить ее график.
и построить ее график.
Решение. 1˚. Область определения  , т.е.
, т.е.  .
.
2˚. Выполняется условие  , следовательно, функция четная и ее график симметричен относительно оси ординат.
, следовательно, функция четная и ее график симметричен относительно оси ординат.
3˚.Нули функции (точки пересечения с осями координат): 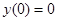 . То есть точка пересечения одна
. То есть точка пересечения одна  .
.
4˚. Вертикальные асимптоты cледует искать в точках разрыва функции  . Рассмотрим односторонние пределы функции
. Рассмотрим односторонние пределы функции
 и
и  , т.к. пределы бесконечны, то прямая
, т.к. пределы бесконечны, то прямая 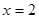 есть вертикальная асимптота. В силу симметрии графика прямая
есть вертикальная асимптота. В силу симметрии графика прямая  также вертикальная асимптота.
также вертикальная асимптота.
5˚. Рассмотрим поведение функции при  .
.
Вычислим  , отсюда следует, что горизонтальных асимптот нет, нужно искать наклонные асимптоты
, отсюда следует, что горизонтальных асимптот нет, нужно искать наклонные асимптоты  :
:
|
|
|
 .
.
Наклонной асимптоты также нет.
6˚. Экстремумы и интервалы монотонности.
Найдем 
 при
при 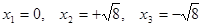 - критические точки и
- критические точки и  - точки разрыва функции.
- точки разрыва функции.
Из рисунка 4 видно, что точки  являются точками минимума и
являются точками минимума и  , а точка
, а точка 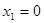 – точка максимума и
– точка максимума и  .
.
На интервалах  функция убывает, а на интервалах
функция убывает, а на интервалах  – возрастает.
– возрастает.
7˚. По результатам исследования построим график. График изображен на рисунке.

7.3. Дифференциал функции
Определение. Дифференциалом функции называется главная, линейная относительно 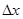 часть приращения функции, равная произведению производной на приращение независимой переменной:
часть приращения функции, равная произведению производной на приращение независимой переменной:
 .
.
Определение. Дифференциал независимой переменной 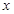 равен приращению этой переменной
равен приращению этой переменной

Тогда формулу для дифференциала функции можно записать в виде:

Приближенные вычисления с помощью дифференциала.
 ,
,
 .
.
 .
.
Пример. Вычислить приближенно 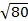
Решение. В нашем случае 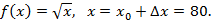
Надо так подобрать  (
( должно быть близко к
должно быть близко к 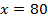 ), чтобы
), чтобы  извлекался точно. Очевидно, что
извлекался точно. Очевидно, что  Тогда
Тогда
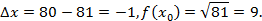
Чтобы применить формулу, вычислим производную

и найдём значение производной в точке 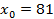 :
:

Тогда получим:

|
|
|


