 |
Предел числовой последовательности и функции
|
|
|
|
Число 
называется пределом функции 
при 
, если для любого, сколь угодно малого положительного числа 
, найдется такое положительное число 
(зависящее от 
), что для всех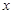 
таких что 
, верно неравенство
.
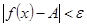Обозначают: 
или 
при .
Число называется пределом функции в точке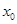 
, если для любого, сколь угодно малого положительного числа , найдется такое положительное число 
(зависящее от ), что для всех 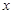, не равных 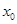и удовлетворяющих условию 
, выполняется неравенство .
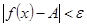Обозначают: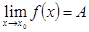 
или при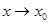 
.
Функция 
называется бесконечно малой величиной при 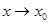или при , если ее предел равен нулю:
.
Функция называется бесконечно большой при 
, если ее предел равен бесконечности:
.
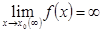Теорема о связи между бесконечно малыми и бесконечно большими величинами.
Если функция есть бесконечно малая величина при 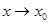(), то функция 
является бесконечно большой при 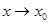(). И, наоборот.
Первым замечательным пределом называется
Вторым замечательным пределом называется предел числовой последовательности 
:
, где 
Если рассмотреть функцию 
, то при функция имеет также предел, равный числу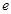 
: 
.
Если существуют 
и 
, то имеют место теоремы о пределах:
1) 
.
2) 
.
3) 
, 
.
4) Если 
, 
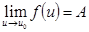, то предел сложной функции 
.
При вычислении пределов часто возникают выражения вида 
, 
, 
, 
, 
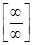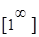. Такая ситуация называется неопределённостью, а поиск предела в этой ситуации – раскрытие неопределённостей.
Задача о непрерывном зачислении процентов
Первоначальный вклад в банк составил 
денежных единиц. Банк выплачивает р % годовых. Необходимо найти размер вклада 
через t лет.
При использовании простых процентов размер вклада ежегодно будет увеличиваться на одну и ту же величину
|
|
|
, т.е.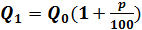 
, 
,…, 
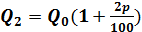При использовании сложных процентов размер вклада ежегодно будет увеличиваться в одно и то же число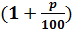 
раз, т.е.
, 
,…, 
.
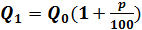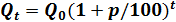Если начислять проценты не один раз в году, а п раз, то при этом же ежегодном приросте р % процент начисления за 1/ п часть года составит р %/ п, а размер вклада за t лет при пt начислениях составит
.
Будем полагать, что проценты по вкладу начисляются каждое полугодие (п = 2), ежеквартально (п = 4), ежемесячно (п = 12), каждый день (п = 365), каждый час (п = 8760) и т.д., непрерывно (п 
). Тогда размер вклада за t лет составит
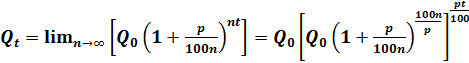
или с учётом второго замечательного предела при 
.
Формула выражает показательный (экспоненциальный) закон роста (при р >0) или убывания (при р <0). Она может быть использована при непрерывном начислении процентов.
Пример. Вычислить предел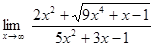 
.
Решение.
=
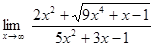Установим тип неопределенности: при 
числитель и знаменатель дроби являются бесконечно большими функциями. Следовательно, имеем неопределенность «
».
= «» =
Для раскрытия неопределенности выделим за скобки старшие степени переменной х как в числителе, так и в знаменателе дроби.
= 
= 
=
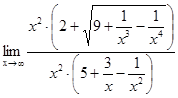Сократим множители 
. Слагаемые 
при являются бесконечно малыми функциями. Таким образом, получим:
.
Пример. Вычислить предел 
.
Решение.
=
Неопределенность «» образована показательными функциями. Для ее раскрытия выделим за скобки наибольшие слагаемые в числителе и знаменателе дроби.
= 
=
Сократим множители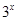 
. Слагаемые 
, 
при являются бесконечно малыми функциями. Таким образом, получим:
= 
= 3.
Пример. Вычислить предел 
.
Решение.
=
Рассмотрим структуру выражения: при 
предел основания степени равен 1, а показатель является бесконечно большой функцией. Таким образом, имеем неопределенность вида «
».
= «» =
Для раскрытия этой неопределенности следует применить формулу 2-го замечательного предела: 
.
а) Выделим в основании степени слагаемое, равное 1:
|
|
|
.
Отметим, что при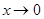 
дробь 
является бесконечно малой функцией.
= 
=
б) Для применения к полученному выражению формулы 2-го замечательного предела необходимо, чтобы показателем степени была бесконечно большая функция 
. С этой целью выполним преобразования:
= 
=
в) Согласно формуле 2-го замечательного предела 
.
Показатель степен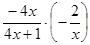и 
при имеет предел:
= 
= 
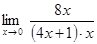= 8.
По теореме о пределе сложной функции получим:
= 
.
Непрерывность функции
Функция 
называется непрерывной в точке 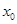, если она удовлетворяет следующим условиям:
1) определена в точке 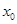, т.е. существует 
;
2) имеет конечные односторонние пределы функции при 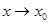слева и справа;
3) эти пределы равны значению функции в точке 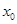, т.е.
.
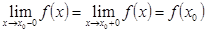Точкой разрыва функции называется точка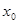 
, в которой не выполняется по крайней мере одно из условий непрерывности.
Причем:
точка 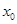- точка разрыва I рода, если существуют конечные односторонние пределы функции, неравные друг другу:
;
точка 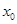- точка разрыва II рода, если хотя бы один из односторонних пределов функции 
или 
равен бесконечности или не существует.
|
|
|
