 |
Критерий невырожденности квадратной матрицы
|
|
|
|
Определение. Квадратная матрица А называется невырожденной, если её строки линейно независимы, и вырожденной в противном случае.
Условие невырожденности квадратной матрицы А порядка п, как нетрудно видеть, равносильно тому, что ранг матрицы А равен п.
Теорема. Для любой невырожденной матрицы А существует обратная матрица 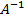 .
.
Теорема. Квадратная матрица А невырождена тогда и только тогда, когда её определитель 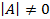 .
.
Нахождение ранга матрицы
Ранг матрицы  находят либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор
находят либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор  k -го порядка матрицы
k -го порядка матрицы  , отличный от нуля, то требуют вычисления лишь миноры (k +1)-го порядка, окаймляющие минор
, отличный от нуля, то требуют вычисления лишь миноры (k +1)-го порядка, окаймляющие минор  , т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен
, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен  .
.
3. Критерий существования ненулевых решений однородной системы линейных алгебраических уравнений с n неизвестными, состоящей из n уравнений
Для того, чтобы однородная система  линейных уравнений с
линейных уравнений с  неизвестными (матрица системы A – квадратная) имела нетривиальное решение, необходимо и достаточно, чтобы определитель матрицы этой системы был равен нулю:
неизвестными (матрица системы A – квадратная) имела нетривиальное решение, необходимо и достаточно, чтобы определитель матрицы этой системы был равен нулю: 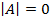 .
.
Нахождение обратной матрицы
Теорема. Если 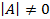 , то матрица
, то матрица
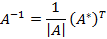
является обратной для А, где матрица  называется присоединённой для А.
называется присоединённой для А.
Пример. Проверить, что матрица
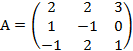
является невырожденной, и найти 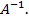
Решение. 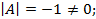



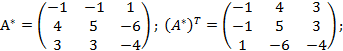
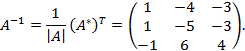
Простейшие матричные уравнения
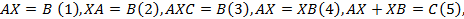
где  – матрицы таких размеров, что все используемые операции возможны, а левые и правые части этих матричных уравнений представляют собой матрицы одинаковых размеров.
– матрицы таких размеров, что все используемые операции возможны, а левые и правые части этих матричных уравнений представляют собой матрицы одинаковых размеров.
|
|
|
Решение уравнений (1)-(3) возможно с помощью обратных матриц в случае невырожденности матриц при Х. В общем случае матрицу Х записывают поэлементно и проводят указанные в уравнении действия над матрицами. В результате получают систему линейных уравнений. Решив систему, находят элементы матрицы Х.
Тема 2. Системы линейных уравнений
Системой 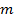 линейных алгебраических уравнений с
линейных алгебраических уравнений с  неизвестными называется система уравнений вида
неизвестными называется система уравнений вида
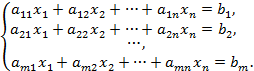
Здесь числа  (
( ;
;  ) называются коэффициентами системы;
) называются коэффициентами системы; 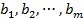 – свободными членами;
– свободными членами; 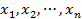 – неизвестными.
– неизвестными.
Матричная запись системы
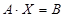 , где
, где
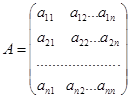
| - матрица коэффициентов при переменных, | |

| - матрица-столбец переменных, | |
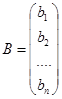
| - матрица столбец свободных членов. | |
Решением системы называется упорядоченная совокупность  чисел
чисел 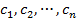 такая, что после замены неизвестных
такая, что после замены неизвестных 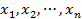 соответственно числами
соответственно числами 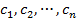 каждое уравнение системы превращается в верное числовое равенство.
каждое уравнение системы превращается в верное числовое равенство.
Система называется совместной, если она имеет хотя бы одно решение.
Если система не имеет ни одного решения, то она называется несовместной.
Совместная система называется определенной, если она имеет единственное решение.
Если же у системы есть хотя бы два различных решения, то она называется неопределенной.
Система называется однородной, если все свободные члены равны нулю. В противном случае, систему называют неоднородной.
Системы линейных уравнений называются эквивалентными, если множество их решений совпадает, то есть любое решение одной системы одновременно является решением другой, и наоборот. Вопрос о разрешимости системы линейных уравнений в общем виде рассматривается в следующей теореме.
Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.
Для совместных систем линейных уравнений верны следующие теоремы.
|
|
|
1. Если ранг матрицы совместной системы равен числу переменных, т.е.  , то система имеет единственное решение.
, то система имеет единственное решение.
2. Если ранг матрицы совместной системы меньше числа переменных, т.е. 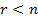 , то система неопределённая и имеет бесконечное множество решений.
, то система неопределённая и имеет бесконечное множество решений.
Пусть 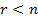 ;
; 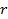 перменных
перменных  называют основными или базисными, если определитель матрицы из коэффициентов при них (т.е. базисный минор) отличен от нуля. Остальные
называют основными или базисными, если определитель матрицы из коэффициентов при них (т.е. базисный минор) отличен от нуля. Остальные  называются неосновными или свободными.
называются неосновными или свободными.
Решение системы, в котором все  неосновных переменных равны нулю, называются базисным.
неосновных переменных равны нулю, называются базисным.
Т.к. каждому разбиению переменных на основные и неосновные соответствует одно базисное решение, а число способов разбиения не превосходит числа сочетаний, то и базисных решений имеется не более  . Таким образом, совместная система т линейных уравнений с п переменными (т < n) имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее
. Таким образом, совместная система т линейных уравнений с п переменными (т < n) имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее  , где
, где 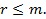
Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений даёт систему, эквивалентную исходной. Опираясь на эти свойства, исходную систему уравнений можно преобразовать к виду:

Здесь неизвестные  , называются базисными переменными, остальные неизвестные
, называются базисными переменными, остальные неизвестные  – свободными переменными.
– свободными переменными.
Сами равенства, выражающие базисные переменные через свободные, называются общим решением системы. Решение системы, получающееся при задании конкретных значений свободных переменных, называется частным решением системы.
Может случиться так, что все неизвестные 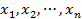 окажутся базисными переменными, тогда система уравнений будет иметь единственное решение:
окажутся базисными переменными, тогда система уравнений будет иметь единственное решение:
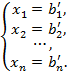
При  решение системы трех уравнений
решение системы трех уравнений

имеет наглядный геометрический смысл. Каждое из трех этих уравнений определяет плоскость. Геометрическое место точек пересечения плоскостей является решением этих уравнений. Если существует только одна точка пересечения плоскостей, то система является определенной, она имеет единственное решение. Если все три плоскости пересекаются вдоль прямой, то система имеет бесконечное множество решений, она является неопределенной. Если две (или все три) плоскости параллельны, то система не имеет ни одного решения, она является несовместной.
|
|
|

Рис.1 Система трех линейных уравнений от трёх переменных определяет набор
плоскостей. Точка пересечения плоскостей является решением этих уравнений.
Пример. Методом Гаусса решить систему линейных уравнений:

Решение. Следуя Гауссу, будем проводить преобразования не самих уравнений, а свободных членов и коэффициентов системы:

Первую строку умножим на  и результат сложения полученной строки с второй строкой поместим на место второй строки. Первую строку умножим на
и результат сложения полученной строки с второй строкой поместим на место второй строки. Первую строку умножим на  и результат сложения полученной строки с третьей строкой поместим на место третьей строки. Получим:
и результат сложения полученной строки с третьей строкой поместим на место третьей строки. Получим:
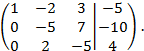
Вторую строку, умноженную на 2, сложим с третьей строкой, умноженной на 5. Результат сложения поместим на место третьей строки. Получим:

Третью строку поделим на 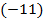 и результат деления оставим на этом же месте. Затем третью строку, умноженную на
и результат деления оставим на этом же месте. Затем третью строку, умноженную на 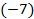 , сложим с второй строкой и результат сложения поместим на место второй строки. После этого третью строку, умноженную на
, сложим с второй строкой и результат сложения поместим на место второй строки. После этого третью строку, умноженную на 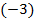 , сложим с первой строкой и результат сложения поместим на место первой строки. Получим:
, сложим с первой строкой и результат сложения поместим на место первой строки. Получим:
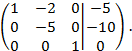
Вторую строку поделим на  и результат деления оставим на этом же месте. Затем вторую строку, умноженную на
и результат деления оставим на этом же месте. Затем вторую строку, умноженную на 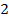 , сложим с первой строкой и результат сложения поместим на место первой строки. Получим новую совокупность свободных членов и коэффициентов системы:
, сложим с первой строкой и результат сложения поместим на место первой строки. Получим новую совокупность свободных членов и коэффициентов системы:

соответствующую следующей системе уравнений:

Отсюда следует, что 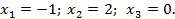
Проверка: Найденные значения 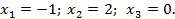 подставим в левую часть исходной системы уравнений:
подставим в левую часть исходной системы уравнений:
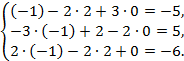
Полученные значения сравним со значениями в правых частях исходной системы уравнений. Совпадение указывает на правильность полученного решения.
Ответ: Система линейных уравнений

имеет решение: 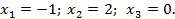
Пример. Методом Гаусса решить систему трех уравнений с четырьмя неизвестными:
|
|
|

Решение. Следуя Гауссу, будем проводить преобразования не самих уравнений, а свободных членов и коэффициентов системы:
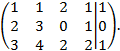
Первую строку умножим на  , затем результат сложения полученной строки со второй строкой поместим на место второй строки. Первую строку умножим на
, затем результат сложения полученной строки со второй строкой поместим на место второй строки. Первую строку умножим на 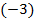 и результат сложения полученной строки с третьей строкой поместим на место третьей строки. Получим:
и результат сложения полученной строки с третьей строкой поместим на место третьей строки. Получим:
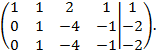
Две последних строки оказались одинаковыми. Это означает, что с помощью элементарных преобразований исходную систему уравнений удалось преобразовать к виду:

в котором третье и второе уравнение одинаковы. Следовательно, имеет смысл проводить преобразования свободных членов и коэффициентов первого и второго уравнений:
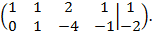
Вторую строку умножим на 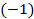 , затем результат сложения полученной строки с первой строкой поместим на место первой строки. Получим:
, затем результат сложения полученной строки с первой строкой поместим на место первой строки. Получим:
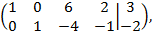
что соответствует системе следующих уравнений:
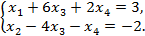
Отсюда следует, что 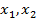 являются базисными переменными. Представим их через
являются базисными переменными. Представим их через  :
:

Остальные неизвестные  являются свободными переменными. Таким образом, система исходных уравнений имеет бесконечное множество решений:
являются свободными переменными. Таким образом, система исходных уравнений имеет бесконечное множество решений:
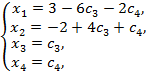
где  и
и  могут принимать любые значения из интервала
могут принимать любые значения из интервала  .
.
Проверка: Найденные значения подставим в левую часть исходной системы уравнений:

Полученные значения сравним со значениями в правых частях исходной системы уравнений. Совпадение указывает на правильность полученного решения.
Ответ: Система линейных уравнений

имеет бесконечное множество решений:
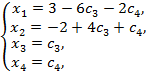
где  и
и  могут принимать любые значения из интервала
могут принимать любые значения из интервала  .
.
Пример. Методом Гаусса решить систему четырех уравнений с пятью неизвестными:

Решение. Следуя Гауссу, будем проводить преобразования не самих уравнений, а свободных членов и коэффициентов системы:
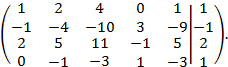
Первую строку сложим со второй строкой, результат сложения поместим на место второй строки. Первую строку умножим на  и результат сложения полученной строки с третьей строкой поместим на место третьей строки. Получим:
и результат сложения полученной строки с третьей строкой поместим на место третьей строки. Получим:

Результат сложения третьей строки с четвертой строкой поместим на место четвертой строки. Получим:
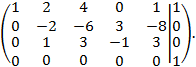
Обратим внимание на четвертую строку, значения в которой позволяют представить последнее уравнение системы в виде:
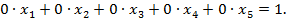
Заметим, что это равенство не выполняется ни при каких значениях переменных, поскольку 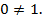 Следовательно, система исходных уравнений не имеет решений.
Следовательно, система исходных уравнений не имеет решений.
Ответ: Система линейных уравнений

не имеет решений.
|
|
|


