 |
Нахождение обратной матрицы с помощью элементарных преобразований.
|
|
|
|
Пусть А – невырожденная матрица (понятие невырожденности появится позже). Припишем к ней (например, справа) единичную матрицу Е. Далее с помощью элементарных преобразований над строками «сдвоенной матрицы (А│E) приводим А («левую половину») к единичной матрице Е. Тогда на месте первоначально приписанной матрицы Е окажется матрица А-1.
Заметим, что из самого способа нахождения матрицы А-1 легко следует, что матрица, обратная для А-1, есть А. Действительно, проделав преобразования, переводящие А в Е, в обратном порядке, из матрицы Е получим А, а из А-1 матрицу Е. это означает, что А есть обратная матрица для А-1, т.е. А-1А = Е.
Пример. Для матрицы
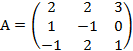
Найти обратную матрицу А-1.
Решение. Составим матрицу
.
С помощью элементарных преобразований приведём её левую «половину» А к матрице Е:
 | |||||||
 | |||||||
 | |||||||
 | |||||||
 | |||
 | |||
Правее вертикальной черты получилась обратная матрица А-1:
Способ решения уравнения АХ = В
Пусть А – невырожденная матрица. Приведём её с помощьюэлементарных преобразований над строками к единичной матрице Е. Если затем те же самые преобразования применить к строкам матрицы В, то получим искомую матрицу Х.
Заметим, что нет необходимости специально запоминать преобразования, совершенные над А, чтобы проделать их над В. Вместо этого можно приписать к А (например, справа) матрицу В
(А|В)
и выполнять преобразования сразу над «сдвоенной» матрицей. После того как левая половина приведётся к Е, правая приведётся к искомой матрице Х.
Пример. Решить уравнение
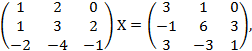
где Х – неизвестная матрица 
.
Решение. Имеем
|
|
|
Правее вериткальной черты получилась искомая матрица
Определители и их свойства
Непосредственное вычисление определителей второго и третьего порядка. Формула разложения определителя по строкам и столбцам.
Каждой квадратной матрице 
по некоторому закону может быть поставлено в соотвествие число 
, называемое определителем матрицы А или просто определителем п-го порядка. Обозначают: 
1) Определителем матицы 1-го порядка 
, называется элемент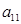 
.
2) Определителем матрицы 2-го порядка называется число, вычисляемое по формуле:
.
Пример. Вычислить определитель матрицы 
.
Решение.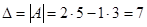 
.
3) Определителем матрицы 3-го порядка называется число, вычисляемое по формуле:
Данная формула получила название правила треугольников.
 |
Пример. Вычислить определитель 
.
Решение. 
.
4) Определитель квадратной матрицы 
-го порядка (определитель -го порядка).
Определение 21. Минором 
элемента 
матрицы -го порядка называется определитель матрицы 
-го порядка, полученной из матрицы 
вычеркиванием 
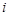-й строки и 
-го столбца.
Определение 22. Алгебраическим дополнением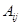 
элемента матрицы -го порядка называется минор, взятый со знаком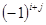 
:
.
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
(разложение по элементам 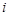-й строки; 
).
(разложение по элементам -го столбца; 
).
Свойства определителей
1. Если какая-либо строка (столбца) матрицы состоит из одних нулей, то ее определитель равен 0.
2. Если все элементы какой-либо строки (столбца) матрицы умножить на число 
,то ее определитель умножится на это число .
Замечание. За знак определителя можно выносить общий множитель любой строки (столбца) в отличие от матрицы, за знак которой можно выносить общий множитель всех элементов.
3. При транспонировании матрицы ее определитель не изменяется: 
.
|
|
|
4. При перестановки двух строк(столбцов) матрицы ее определитель меняет знак на противоположный.
5. Если матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.
6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
7. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0.
8. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
9. Сумма произведений произвольных чисел 
на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки(столбца) на числа 
10. Определитель произведения двух квадратных матриц равен произведению их определителей: 
– матрицы п –го порядка.
Применение определителей
|
|
|
