 |
Тема 8. Интегральное исчисление функций одной переменной
|
|
|
|
Неопределённый интеграл
Определение. Функция 
называется первообразной функцией для функции 
на промежутке 
, если в каждой точке этого промежутка 
.
Определение. Совокупность всех первообразных функции на промежутке называется неопределенным интегралом от функции и обозначается 
, где
- знак интеграла,
- подынтегральная функция,
- подынтегральное выражение.
Таким образом:
,
где - некоторая первообразная для , 
произвольная постоянная.
Свойства неопределенного интеграла
1) Производная от неопределенного интеграла равна подынтегральной функции, т.е.
.
2) Дифференциал неопределенного интеграла равен подинтегральному выражению, т.е.
d dx.
3) Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.
.
4) Постоянный множитель можно выносить за знак интеграла, т.е.
.
5) Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.
.
Некоторые табличные интегралы
 ,
|  ,
|
 ,
|  ,
|
| 
|
 .
| 
|
| 
|
 ,
|  .
|
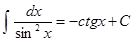 +c,
|  +c,
|
1) Метод замены переменной (метод подстановки).
Пусть заданный интеграл не может быть непосредственно преобразован к табличному интегралу. Введем новую переменную 
: 
. Тогда 
, 
,
.
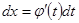Теорема. Пусть некоторая первообразная для функции . Тогда если вместо аргумента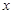 
подынтегральной функции и первообразной подставить выражение 
, то это приведет к появлению дополнительного множителя 
перед первообразной: 
, где 
и 
- некоторые числа, 
.
2) Метод интегрирования по частям.
Пусть 
и 
- дифференцируемые функции. Тогда 
Интегрируя левую и правую часть, имеем
|
|
|
, или
.
Полученная формула называется формулой интегрирования по частям для неопределенного интеграла.
Пример 1. Вычислить интеграл 
.
Решение. 
.
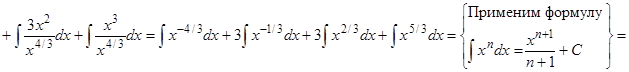
Пример 2. Вычислить интеграл 
.
Решение.
.
Пример 3. Вычислить интеграл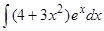 
.
Решение.
.
8.2. Определенный интеграл
Определение. Определенным интегралом от функции 
на отрезке 
называется предел интегральной суммы при 
, т.е.
.
- нижний предел,
- верхний предел,
- подынтегральная функция,
- подынтегральное выражение.
Геометрический смысл определенного интеграла
Пусть на отрезке задана неотрицательная функция . Тогда площадь 
криволинейной трапеции, ограниченной кривой , прямыми 
, 
и осью абсцисс 
(рис.10.2) численно равна определенному интегралу от функции на .
|
|
Свойства определенного интеграла
1) Постоянный множитель можно выносить за знак интеграла:
.
2) Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций:
.
3) При перестановке пределов интегрирования знак определенного интеграла меняется на противоположный:
.
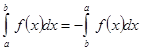4) Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей:
.
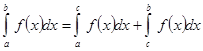5) Если на отрезке , где 
, 
, то и
,
т.е. обе части неравенства можно почленно интегрировать.
Теорема. Пусть функция непрерывна на отрезке и - любая первообразная для на . Тогда определенный интеграл от функции на отрезке равен приращению первообразной на этом отрезке, т.е.
.
Теорема. Пусть функция 
имеет непрерывную производную на отрезке 
при условии 
и 
, а данная функция непрерывна в каждой точке 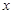вида , где 
. Тогда справедливо следующее равенство
-
Формула замены переменной в определенном интеграле.
Пример. Вычислить определенный интеграл 
.
Решение.
.
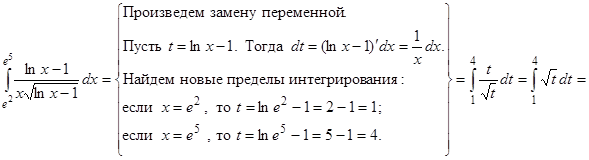
Пример. Вычислить площадь фигуры, ограниченной линиями:
|
|
|
Решение. Для построения фигуры найдем точку пересечения линий 
:
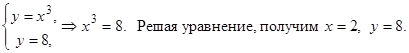
Данная фигура ограничена двумя линиями 
(сверху), 
(снизу) и двумя вертикальными прямыми 
и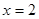 
. Следовательно, согласно формуле 
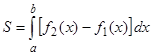, имеем
.
Вычислить определенный интеграл 
.
Решение.
= 
.
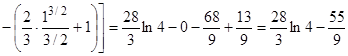Несобственный интеграл
Определение. Несобственным интегралом с бесконечным верхним пределом 
от непрерывной функции на полуинтервале 
называется предел интеграла 
при стремящемся к 
:
.
Если этот предел существует, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.
Аналогично определяется несобственный интеграл от непрерывной функции с бесконечным нижним пределом интегрирования, а именно
.
Несобственный интеграл с двумя бесконечными пределами интегрирования обозначается символом
, где 
.
Пример. Вычислить несобственный интеграл 
.
Решение.
.
|
|
|
