 |
Необходимый признак сходимости
|
|
|
|
Теорема. Если ряд сходится, то предел его общего члена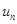 
при 
равен нулю
.
Достаточные признаки сходимости ряда с положительными членами
1) I - й признак сравнения.
Пусть даны два ряда с положительными членами: 
(1) и 
(2), причем члены 1-го ряда не превосходят членов 2-горяда, т.е. при любом 
.
Тогда а) если сходится ряд (2), то сходится и ряд (1),
б) если расходится ряд (1), то расходится и ряд (2).
Отметим «эталонные» ряды, часто используемые для сравнения:
а) геометрический ряд 
- сходится при 
, расходится при 
,
б) гармонический ряд 
- расходится,
в) обобщенный гармонический ряд
сходится при 
, расходится при 
.
2) II - й признак сравнения.
Есл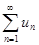и 
и 
- ряды с положительными членами и существует конечный предел отношения их общих членов 
, то ряды одновременно сходятся, либо расходятся.
3) Признак Даламбера.
Пусть для ряда 
с положительными членами существует предел отношения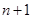 
члена к -му члену: 
.
Тогда, если 
, то ряд сходится, если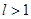 
, то ряд расходится, если 
, то вопрос о сходимости ряда остается открытым.
Интегральный признак сходимости.
Пусть дан ряд , члены которого положительны и не возрастают, т.е. 
, а функция 
, определенная при 
, непрерывная и не возрастающая и 
.
Тогда для сходимости ряда необходимо и достаточно, чтобы сходился несобственный интеграл 
.
Определение. Под знакочередующимся рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны:
, где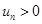 
.
Теорема (признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине 
и предел его общего члена при равен нулю, т.е. , то ряд сходится, а его сумма не превосходит первого члена: 
.
|
|
|
Следствие. Погрешность при приближенном вычислении суммы сходящегося знакочередующегося ряда, удовлетворяющего условиям признака Лейбница, по абсолютной величине не превышает абсолютной величины первого отброшенного члена.
Знакопеременные ряды
Определение. Под знакопеременным рядом 
понимается ряд, в котором любой член может быть как положительным, так и отрицательным.
Теорема (достаточный признак сходимости знакопеременного ряда). Если ряд, составленный из абсолютных величин членов знакопеременного ряда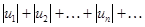 
сходится, то сходится и исходный ряд.
Определение. Ряд называется абсолютно сходящимся, если ряд, составленный из абсолютных величин его членов, сходится.
Определение. Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Пример. Исследовать сходимость числового ряда 
.
Решение. Проверим выполнение признака Коши.
,
так как предел меньше 1, то ряд сходится.
Пример. Исследовать сходимость числового ряда 
.
Решение. Проверим выполнение признака Даламбера.
, то по признаку Даламбера ряд сходится.
Заметим, что 
Пример. Исследовать сходимость числового ряда 
. В случае сходимости ряда установить ее характер (абсолютная или условная).
Решение. Проверим признак Лейбница. Вычислим члены ряда по абсолютной величине 
Они убывают, начиная с третьего. Вычислим предел общего члена, применив правило Лопиталя
.
Таким образом, ряд сходится по признаку Лейбница. Ряд 
, составленный из абсолютных величин данного ряда, расходится, так как его можно сравнить с расходящимся гармоническим рядом 
, применив предельный признак сравнения
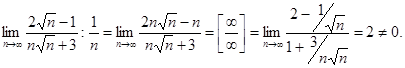
10.2 Степенные ряды
Определение. Ряды, членами которых являются функции, называются функциональными, в частности, если членами ряда являются степенные функции, то такие ряды называются степенными:
|
|
|
(10.4)
где числа 
- коэффициенты ряда.
Определение. Совокупность тех значений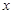 
, при которых степенной ряд (10.4) сходится, называется областью сходимости степенного ряда.
Теорема Абеля. 1) Если степенной ряд сходится при значении 
(отличном от нуля), то он сходится и, притом абсолютно, при всех значениях 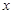таких, что 
.
2) Если степенной ряд расходится при 
, то он расходится при значениях 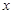таких, что 
.
Следствие. Из теоремы Абеля следует, что существует такое число 
, что при 
ряд сходится, а при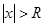 
- расходится.
| Число  получило название радиуса сходимости, а интервал  - интервал сходимости степенного ряда (рис. 14.1).
На концах отрезка  ряд может как сходиться, так и расходиться.
|
радиус сходимости
. (10.5)
разложение функции в ряд Маклорена:
, (10.6)
где 
.
Так же как и для числовых рядов сумму ряда Маклорена можно представить в виде
,
где 
- n-я частичная сумма ряда, 
- -й остаток ряда.
Теорема. а) Для того, чтобы ряд Маклорена сходился к функции , необходимо и достаточно, чтобы при остаток ряда стремился к нулю, т.е.
для всех значений 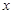из интервала .
б) Если функция разложена в ряд Маклорена, то это разложение единственное.
|
|
|
