 |
Задачи и упражнения для самостоятельного решения
|
|
|
|
1. Приведите к линейному виду уравнение Аррениуса 
, где k и Т – переменные величины.
2. Линеаризуйте уравнение для расчета константы диссоциации слабого электролита 
, где K дис (константа диссоциации) и λ0 (эквивалентная электрическая проводимость при бесконечном разбавлении) – величины постоянные.
3. Приведите к линейному виду следующее уравнение
,
если Kс >>1; σ и с – переменные величины.
Нахождение производных и интегрирование
Операции нахождения производных и интегрирования используются во многих разделах курса физической и коллоидной химии. Это связано с тем, что многие законы имеют наиболее простой вид в форме дифференциальных уравнений, которые содержат производные. Для получения соответствующих алгебраических уравнений дифференциальные уравнения интегрируются. Методы нахождения производной в курсе физической и коллоидной химии применяются для расчета зависимости константы равновесия реакции от температуры (уравнения изобары и изохоры), расчета скорости химической реакции и в других случаях.
Нахождение производной можно проводить разными способами: а) по графику; б) по таблице; в) аналитически по формуле.
Для нахождения производной функции в некоторой точке графическим методом строим график этой функции по экспериментальным данным (рис.38) и проводим касательную к кривой в заданной точке.
Рис. 38. Геометрический смысл производной
Выберем две произвольные точки (1 и 2), на этой касательной, которые должны находится на возможно большем расстоянии друг от друга для повышения точности расчета, и определим их координаты. Далее рассчитываем производную по формуле (21):
 ,
| (21) |
.
|
|
|
Нахождение производной по табличным данным заключается в том, что расчеты проводит непосредственно по таблице, используя формулу (21), без построения графика (см. Пример решения задачи 3).
Аналитический метод нахождения производных основан применении основных формул дифференциального исчисления (Приложение, таблица 3).
Методы интегрирования широко применяются в курсе физической и коллоидной химии для решения дифференциальных уравнений. Например, в термодинамике они используются для определения зависимости энтальпии химической реакции от изменения теплоемкости в процессе протекания химической реакции. В химической кинетике – для вывода уравнений позволяющих рассчитывать концентрации веществ, участвующих в реакции от времени, например, зависимость количества сахарозы, которое инвертировалось к моменту времени t и в других случаях.
Примеры решения задач
1. Рассчитайте изменение энтальпии 1 моля кристаллического магния в процессе его нагревания от 315 до 465 К по формуле 
с учетом зависимости мольной теплоемкости от температуры: 
.
Решение:
2. Зависимость константы равновесия реакции от температуры выражается уравнением:
Найдите производную d ln Kр / dT.
Решение:
Для перехода от десятичного логарифма к натуральному, умножим обе части уравнения на 2,303:
Применяя формулы для нахождения производных, получим:
3. Рассчитайте скорость химической реакции и постройте график зависимости скорости от времени по таблице, используя формулу 
, где υ – скорость химической реакции, ммоль/(л×с), c –концентрация, t – время:
| № | ||||||
| t, с | ||||||
| с, ммоль/л | 19,8 | 14,7 | 11,0 | 9,15 | 7,72 | 5,88 |
Решение:
Рассчитаем скорость химической реакции (уравнение(21)):
,
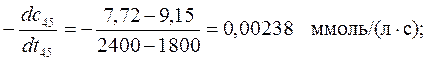
Для построения графика зависимости скорости химической реакции от времени рассчитываем среднее время как полусумму времени двух соседних точек, так как наклон касательной совпадает с наклоном секущей в средней точке:
|
|
|
Для построения графика внесем полученные результаты в таблицу.
| № | υ ·103, ммоль/(л×с) | t ср, с |
| 8,5 | ||
| 6,1 | ||
| 3,15 | ||
| 2,38 | ||
| 1,53 |
Строим график зависимости «υ – t» (рис. 39).
Рис. 39.Зависимость скорости реакции от времени
|
|
|
