Перепишем это уравнение в виде

, (6.22)

где c_w - коэффициент консолидации;

(6.23)

Уравнение (6.22) и есть уравнение фильтрационной консолидации грунтов для плоской задачи. Его решение с учетом начального порового давления (при t = 0) и граничных условий задачи позволяет определить поровое давление и как функцию координат и времени. Тотальные напряжения находятся из решения соответствующей задачи без учета консолидации, их эффективные части определяются с учетом равенства (6.1), а соответствующие им деформации — равенствами (6.17) или (6.18). В конечном счете, с помощью зависимостей Коши (3.17) могут быть вычислены перемещения точек массива и, в частности, осадки поверхности основания. Очевидно, перемещения и осадки будут не только функциями координат, но и времени даже в тех случаях, когда приложенные к основанию внешние нагрузки остаются постоянными. Ясно также, что перемещения и осадки будут нарастать в процессе консолидации с затухающей скоростью и стремиться к своим конечным значениям при t → ∞

 

6.4. Задачи о сосредоточенной силе и водопроницаемых полосовых нагрузках

Аналитическое решение плоской задачи фильтрационной консолидации, т.е. решение уравнения (6.22) с учетом начальных (t = 0) и граничных (z = 0) условий, представляет большие трудности. Необходимый для этого математический аппарат выходит за рамки курса высшей математики, который изучается в строительных вузах. Поэтому здесь приведем решения плоских задач без вывода. Фундаментальное значение имеет задача определения порового давления в водонасыщенном однородном основании, к поверхности которого в момент времени t = 0 приложена равномерная сосредоточенная сила Р, остающаяся далее постоянной. Граничные условия этой задачи совпадают с задачей Фламана. Следовательно, согласно п. 6.2, начальное распределение порового давления должно быть равно распределению среднего напряжения в задаче Фламана для консолидирующегося основания. Поскольку в задаче Фламана = 0, то в соответствии с формулами (6.21) в момент t = 0 имеем

(6.24)

где

Решение поставленной задачи для любого момента времени имеет вид:

(6.25)

При λ = 1, что соответствует v = 0,5, решение было получено В.Т. Короткиным в 1951 г. Введенный коэффициент λ < 1 уточняет решение В.Г. Короткина и улучшает соответствие теории экспериментам.

Для того, чтобы наглядно охарактеризовать распределение порового давления в основании в соответствии с решением В.Г. Короткина (5.34) при λ = 1, на рис. 6.6 в правой половине основания представлены эпюры изменения u от силы Р, численно равной числу π. Эпюры построены в двух горизонтальных и одном вертикальном сечениях на моменты времени t, определенные равенствами = 0; 1 и 4 м2. Как видно, в горизонтальных сечениях u имеет максимальное значение в точках оси и асимптотически стремится к нулю при | x | → ∞.

 

Рисунок 6.6. - Распределение порового давления в плоской задаче о погонной

нагрузки на основание

 

В вертикальном сечении при t > 0 поровое давление равно нулю на поверхности основания, затем нарастает до некоторого максимального значения, а далее асимптотически убывает до нуля при z → ∞.

Переходя к полосовым нагрузкам, отметим, что при определении порового давления в процессе фильтрационной консолидации основания важную роль играют граничные условия поверхности основания по водопроницаемости. В этом смысле полосовые нагрузки можно подразделить на водопроницаемые и водонепроницаемые. В первом случае водопроницаемость поверхности основания принимается везде одинаковой, в том числе и в пределах полосы загружения. Во втором случае водопроницаемость поверхности основания сохраняется только за пределами полосы загружения.

Решение консолидационной задачи от полосовой водопроницаемой нагрузки может быть получено с помощью решения В.Г. Короткина. Для этого поступим аналогично тому, как в разд. 4 с помощью формулы Фламана определялось напряженное состояние основания от полосовых нагрузок, но ради краткости ограничимся случаем равномерного давления p ₀. Итак, предположим, что в момент времени t = 0 к поверхности основания приложено равномерное полосовое давление интенсивностью p ₀, которое в дальнейшем остается постоянным. На расстоянии ξ в этой полосе выделим элементарную полосу шириной dξ. Действие сплошной нагрузки в пределах полосы заменим сосредоточенной силой dP = p₀dξ. Расстояние от этой силы до произвольной точки М в основании определяется координатой z и разностью х - ξ. Используя формулу (6.25), определим бесконечно малую величину порового давления от силы dР в точке М:

Полную величину порового давления, очевидно, получим интегрированием этого выражения по ширине полосы загружения:

(6.26)

Этот интеграл не выражается в аналитическом виде. Но при необходимости его можно вычислить приближенно, заменив интегрирование суммированием. На рис. 6.7 показаны линии равных значений порового давления в долях от приложенного давления, определенные численным методом. Заметим, что ось х в этой и в других задачах с водопроницаемыми полосовыми нагрузками является линией нулевых значений порового давления в любой момент времени.

 

 

Рисунок 6.7. - Линии равных значений порового давления под водопроницаемой

полосовой нагрузкой

 

Очевидно, что с помощью формулы (6.25) и численного метода интегрирования можно определять поровое давление от водопроницаемых полосовых нагрузок при любом сколь угодно сложном законе давления. Этим же методом можно решать задачи и в тех случаях, когда полосовая нагрузка растет во времени по заданному закону. На рис. 6.8 показаны линии равных поровых давлений в основании под водонепроницаемой полосовой нагрузкой в некоторый момент времени, получение которых рассмотрено подробней в п. 7.2.

 

Рисунок 6.8. - Линии равных поровых давлений в основании под водонепроницаемой

полосовой нагрузкой

 

6.5. Расчет осадки в процессе фильтрационной консолидации с использованием метода послойного суммирования

 

Согласно нормам проектирования оснований и фундаментов осадку фундамента считают равной вертикальному перемещению центра его подошвы, т.е. вертикальному перемещению начала координат на рис. 6.9.

 

 

Рисунок 6.9. - К расчету осадок в процессе фильтрационной консолидации

 

При этом расчет осадки выполняют методом послойного суммирования. Поскольку суммирование практически не может быть неограниченным, то осадку подсчитывают до глубины Н_c, которую называют глубиной сжимаемой толщи основания. Предполагается, что вследствие быстрого затухания напряжений в основании по мере удаления от места приложения давления осадка остальной толщи основания мала и ею можно пренебречь. Глубину сжимаемой толщи определяют из условия , где символом обозначено напряжение в природном напряженном состоянии основания. Определение величины Н_c проще всего выполнять графоаналитическим методом, как показано на рис. 6.9.

Поскольку ось Oz является линией симметрии задачи, то в ее точках σ_z = σ_1, σ_x=σ₃, τ_zx = 0. Следовательно, согласно формулам (4.) в точках оси Oz

(6.27)

Значения угла видимости β и его синуса в точках оси z выражается формулами

(6.28)

С учетом этого формулы (6.8) принимают вид:

(6.29)

Линейные относительные деформации ε_z на оси Oz в процессе фильтрационной консолидации определяются вторым из выражений закона Гука. Подставляя в него зависимости (6.16) получим:

(6.30)

Если на оси z выделить элементарный отрезок dz, то абсолютная линейная деформация определяется равенством . Следовательно, осадка точки О в соответствии с принятым допущением определяется интегралом

(6.31)

Разделим сжимаемую толщу на n отрезков размером . В точках деления имеем координату где i = 0,1,..., n.

Обозначим:

(6.32)

где u_i — поровое давление в точках деления оси z в момент t.

Согласно (6.26) в точках деления оси z:

(6.33)

И здесь интегрирование заменим суммированием. Для этого разобьем ширину полосы загружения на полоски шириной . В точках деления , где j = 0,1, …, m.

Обозначим:

(6.34)

В результате согласно формуле трапеций вместо (6.12) имеем:

(6.35)

В конечном счете интеграл (6.31) также будем вычислять по формуле трапеций:

(6.36)

Приведенные формулы позволяют определить протекание осадки основания во времени. Характер зависимости s _i, показан на рис. 6.10. При t > ∞ и u → ∞ и осадка стремится к ее предельному значению s. Указанные расчеты целесообразно выполнять с помощью ЭВМ.

 

 

Рисунок 6.10. - Зависимость осадки консолидирующегося грунта от времени

 

Для произвольных граничных и начальных условий задачи теории фильтрационной консолидации решаются численными методами: методом конечных разностей или методом конечных элементов.

7. Применение численных методов в задачах механики грунтов

7.1. Метод численного интегрирования канонической системы уравнений ТПРГ

 

В общем случае, как отмечалось выше, задачи ТПРГ решаются численным методом интегрирования системы канонических уравнений (5.16):

, ,

.

Напомним, что s - приведенное среднее напряжение, a - угол между осью Oz и направлением первого главного напряжения s₁ (рис. 5.4):

, .

Численный метод позволяет в ходе решения задачи строить конечно-разностную сетку линий скольжения и определять параметры предельного напряженного состояния грунта в узлах сетки. Таким образом, при использовании численного метода вместо непрерывного поля предельных напряжений мы получаем точечное поле. Точность решения той или иной задачи численным методом в определенной степени зависит от выбранной густоты сетки линии скольжения. Для «ручного» счета численный метод слишком трудоемок, но с помощью ЭВМ расчет может выполняться с высокой точностью.

Пусть точка M находится на пересечении двух характеристик 1-го и 2-го семейств (рис. 7.1), и в ближайших к точке M узлах 1 и 2 конечно-разностной сетки, принадлежащих соответствующим характеристикам, известны все параметры канонической системы уравнений - соответственно x ₁, z ₁, a₁, s₁ и x ₂, z ₂, a₂, s₂ (здесь s₁ и s₂ - не главные напряжения (!), а значения среднего приведенного напряжения s в соответствующих точках). Определим величины x, z, a, s в точке M. Следуя известным правилам численного интегрирования, запишем каноническую систему уравнений (5.16), заменив дифференциалы конечными разностями [36]:

, , , .

(7.1)

Кроме дифференциалов искомых функций в выражения (5.16) входят значения функций a и s, которые в (5.17) представлены как 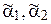и . Это означает, что на характеристике 1-го семейства значения и находятся в интервале [a, a₁] и [s, s₁] соответственно, а и на характеристике 2-го семейства - в интервале [a, a₂] и [s, s₂]. Для этих величин в процессе вычислений нужно применять осреднения, как показано ниже.

 

 

 

Рисунок 7.1. - К численному интегрированию канонической системы уравнений ТПРГ

 

Искомые параметры канонической системы в точке M вычисляются с помощью итераций на каждом шаге интегрирования, по следующим рекуррентным формулам, получаемым из (7.1) (номерами дана последовательность расчета):

	1.	, ,
	2.	, , , ,
	3.	, .

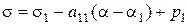На первой итерации принимается

,

на следующих итерациях:

.

Практика вычислений показывает, что, как правило, бывает достаточно трех итераций.

При решении задач ТПРГ сталкиваются с тремя возможными схемами численного решения - тремя краевыми задачами. Схемы интегрирования в пределах краевых задач показаны на рис. 7.2, а, б, в.

Ход решения для первой и второй краевых задач (рис. 5.6, а, б) во многом совпадает: на каждом шаге интегрирования мы имеем значения параметров напряженного состояния в узлах 1 и 2, и по формулам (7.2) определяем эти искомые параметры - x, z, a, s - в неизвестной точке M. Отличие состоит в задании граничных условий для этих краевых задач. Для I краевой задачи должна быть задана некоторая линия (граница), не являющаяся характеристикой (!), на которой в каждой точке определены x, z, a, s (рис. 7.2, а). Обратим внимание на то, что каждая из точек может быть и точкой 1, и точкой 2 в зависимости от того, характеристика какого семейства из нее выходит. Для II краевой задачи должны быть заданы две характеристики разных семейств, причем во всех точках каждой из них известны все параметры напряженного состояния (рис. 7.2, б).

 

 

Рисунок 7.2. - Краевые задачи и последовательность интегрирования: (а) - первая краевая задача, (б) - вторая краевая задача, (в) - третья краевая задача

 

 

Ход построения сетки характеристик несколько отличается в III краевой задаче (рис. 7.2, в). Здесь задана характеристика, в точках которой известны все параметры, и некоторая линия (граница), в точках которой заданы только два из четырех параметров предельного напряженного состояния. Для простоты положим, что, как показано на рис. 7.2, в, линия скольжения 1-го семейства подходит к границе, не являющейся характеристикой, где в каждой точке задано только два из четырех параметров, например, , . Тогда при определении точек, принадлежащих указанной границе, расчет ведется с учетом этих равенств по формулам

	1.	,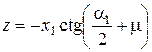
	2.	.

Остальные точки в зоне III краевой задаче рассчитываются по формулам (7.2).

Рассмотрим частный случай II краевой задачи, когда какая-либо линия скольжения, например 1-го семейства, стянута в одну точку A (рис. 7.3). Такие точки называют особыми. Специфика численных решений в этом случае (для схемы на рис. 7.3) заключается в том, что в особой точке для указанной линии скольжения . Следовательно в дифференциальном уравнении вдоль этой линии скольжения будем иметь , а связь параметров a и s дается интегрированием этого уравнения:

 

 

 

Рисунок 7.3. - Вторая краевая задача с особой точкой

 

Каждая характеристика 2 семейства, выходящая из особой точки A определяется своей парой значений и . Величины и отвечают граничной линии второго семейства, параметры которой как правило известны. Далее зона радиального веера раскрывается до пределов, определенных содержанием конкретной задачи. Внутренние точки конечно-разностной сетки линий скольжения находятся с помощью общей системы (7.1) по изложенной выше методике.

Обращаясь к зоне радиального веера в задаче Прандтля, отметим, что на граничной линии () имеем следующие значения переменных и :

Далее следует численное решение в зоне радиального веера , причем в особой точке справедливо соотношение:

 

В данном случае зона радиального веера раскрывается до линии скольжения . Положение этой линии определяется равенством в точке . В численном решении положение этой линии находится подбором.

В задаче о равноустойчивом контуре склона особенность решения заключается в том, что очертание контура заранее неизвестно, оно определится лишь в результате решения.

Определим условия на свободном от нагрузки контуре. Во-первых, среднее приведенное напряжение в любой точке контура определится согласно (5.24):

.

(7.6)

Во-вторых, дифференциальное уравнение контура очевидно выражается формулой:

Пусть в некоторой известной точке контура имеем и . Из этой точки выходит линия скольжения второго семейства, на которой из предыдущего решения будет известна некоторая точка 1. Тогда точка пересечения линии скольжения первого семейства с контуром определится системой:

, , ,

(7.9)

Решение системы осуществляется в следующем порядке:

	1.	, ,	(7.10)
	2.	; ,
	3.	.

На первой итерации принимается , на последующих - .

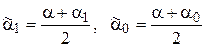Вычисление точек, принадлежащих области ACO, но не лежащих на контуре AO ведется по формулам (7.2).

 

7.2. Решение задач теории фильтрационной консолидации методом конечных разностей

Одним из наиболее общих методов интегрирования дифференциального уравнения фильтрационной консолидации грунта (6.22) является метод конечных разностей, основы которого излагаются далее.

В методе конечных разностей в интегрируемом дифференциальном уравнении производные приближенно выражаются через отношения конечных приращений функций и аргумента. Применительно к уравнению (6.22) это означает, что необходимо заменить на конечные разности производные

При определений разностных отношений ограничимся случаем, когда приращение координат x и z одинаковы (); приращение по времени обозначим Разностное выражение первой производной по времени 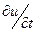представляется очевидным отношением

(7.12)

Разностное выражение для второй производной по координате x в виде

(7.13)

Аналогично

(7.14)

 

Подставив выражения (7.12)...(7.13) в уравнение консолидации (6.22), получим его искомую разностную формулу:

(7.14)

Это уравнение показывает, что в точке х, z можно вычислить поровое давление в следующий момент времени , если в момент t оно известно в этой точке и в четырех соседних, расположенных от нее на расстоянии к влево, вправо, вверх и вниз (рис. 7.4).

Рисунок 7.4. - Расположение узловых точек в расчетах фильтрационной консолидации методом конечных разностей

 

Предположим далее, что нам необходимо численным методом решить некоторую консолидационную задачу, например, консолидационную задачу для основания, нагруженного в момент времени t = 0 равномерным полосовым давлением, остающимся в дальнейшем постоянным. Для ее решения выделим в основании область задачи и введем в ней прямоугольную координатную сетку с шагом размером к в горизонтальном и вертикальном направлениях (см. рис. 7.5). Задача заключается в том, чтобы с помощью уравнения (7.14) определить поровое давление во всех узловых точках сетки в дискретные моменты времени t = τ, 2τ,... вплоть до некоторого конечного времени t _кон = nτ. При этом начальное распределение порового давления в узлах сетки в рассматриваемом примере определяется зависимостью (6.26) при t = 0 и

z > 0:

В узлах, расположенных на свободной поверхности основания, при t > 0 поровое давление принимается равным нулю в течение всего процесса консолидации грунта. На водонепроницаемом участке поверхности основания под подошвой фундамента вводятся фиктивные узлы, в которых поровое давление принимается равным давлению в симметрично расположенных внутренних узлах. Указанный прием позволяет выполнить условие v_z = 0 на этом участке контура.

Вдоль внутренних границ области решения также вводятся дополнительные узлы (см. рис. 7.5), в каждом из которых поровое давление для любого момента времени определяется посредством линейной экстраполяции, исходя из значений его в двух ближайших узлах.

Рисунок 7.5. - Разбивка основания расчетной сеткой в методе конечных разностей

 

Очевидно, решение будет тем точнее, чем гуще принятая сетка и меньше шаг τ. Однако уменьшение их приводит к повышению трудоемкости решения задачи. Кроме того, в математике доказано, что при численном интегрировании уравнений типа (6.22) необходимо выполнять условие

Ясно, что в этом условии выгодно принимать знак строгого равенства. Это дает возможность выбрать максимально допустимый шаг по времени t при назначенном шаге k, что снижает трудоемкость решения задачи. Трудоемкость решения уменьшается и за счет того, что при этом уравнение (7.14) упрощается, принимая вид:

 

7.3. Основы техники вычислений методом конечных элементов

 

Метод конечных элементов (МКЭ) в настоящее время является одним из наиболее популярных численных методов. Основное достоинство МКЭ - его универсальность.

Разобьем некоторую рассчитываемую область основания на треугольные конечные элементы. Рассмотрим простейший треугольный конечный элемент (рис. 7.6) [33].

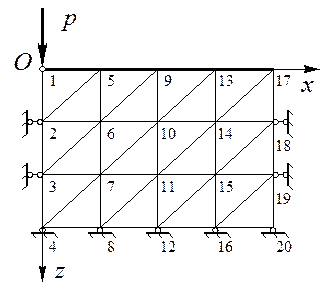
Рисунок 7.6. - Разбивка основания расчетной сеткой в методе конечных элементов

 

Вершины треугольника обозначим i, j, m. Пусть перемещения произвольной точки в этом треугольнике есть линейные функции ее координат (напомним, что u и w - перемещения вдоль осей Ox и Oz):

; .

(7.15)

где - некоторые постоянные в пределах данного элемента коэффициенты.

Тогда перемещения узлов элемента определятся как

(7.16)

Выразим из (7.16) коэффициенты через перемещения узлов:

(7.17)

где:

 

; ; ; ; ; .

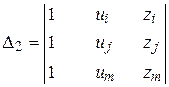(7.18)

 

, площадь треугольника равна .

Далее, выразим перемещения в элементе (7.15) через перемещения его узлов, учитывая (7.15)…(7.18):

;

.

где:

Согласно (4.17) определим относительные деформации:

;

;

,

или, в матричной форме

,

(7.19)

где

, , .

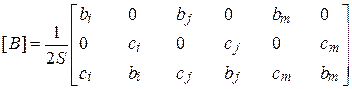Уравнение состояния для отдельного конечного элемента можно записать в виде:

.

(7.20)

В полученном уравнении матрица [ D ] характеризует механические свойства элемента, а матрица [ B ] - его геометрию. В качестве матрицы [ D ], например, в случае линейно-деформируемой среды может быть принята упругая матрица [ D_e ], определяемая с помощью (3.1). Для решения упругопластических задач используется уравнение (7.20) в приращениях.

Работа конечных элементов описывается с использованием равенства работ внутренних и внешних сил. Работу внутренних сил в элементе определим как

.

Так как в пределах элемента принято и , имеем

В соответствии с правилами транспонирования матриц, и учитывая (7.19),

,

откуда

.

(7.21)

Заметим, что в выражении (7.21) значение S площади треугольника должно быть положительным.

Внешнее воздействие на элемент представим в виде сосредоточенных сил, приложенных в узлах i, j и m по направлениям соответствующих узловых перемещений {d _e } (рис. 7.7):

.

Тогда работа внешних сил равна

.

(7.22)

 

Рисунок 7.7. - Простейший конечный элемент

 

 

Сравнивая (7.21) и (7.22), и учитывая (7.20), имеем

,

,

и окончательно

,

(7.23)

где 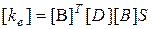- матрица жесткости элемента.

Переходим от рассмотрения отдельного конечного элемента ко всей рассчитываемой области (рис. 7.6). Введем общую нумерацию для всех узлов 1, 2, …, n и составим общую матрицу жесткости [ K ], общую матрицу узловых перемещений { } и общую матрицу узловых сил { R }:

,

(7.23)

где ; ;

Итак, общая матрица перемещений {d} состоит из перемещений всех узлов, расположенных в порядке общей нумерации узлов конечноэлементной сетки. За исключением граничных данных о перемещениях отдельных узлов сетки, эта матрица представляет собой матрицу искомых неизвестных перемещений. Общая матрица узловых сил { R } также включает в себя компоненты этих сил в соответствии с общей нумерацией узлов. Эти величины задаются исходя из граничных условий или в соответствии с массовыми силами, действующими в расчетной области. Если массовые силы отсутствуют, то исходя из условия равновесия всех конечных элементов, их силовое воздействие взаимоуравновешивается и компоненты узловых сил имеют нулевые значения. При наличии массовых сил узловая сила составляет произведение массовой силы на площадь, приходящуюся на этот узел.

Элементы общей (или глобальной) матрицы жесткости выражают собой реакцию по направлению некоторой силы от единичного перемещения в некотором направлении и представляют собой алгебраическую сумму элементов локальных матриц жесткости, в которых присутствуют данные направления узловых сил и перемещений.

В результате решения данной системы получаем перемещения каждого узла конечноэлементной сетки. Затем по формулам (7.19) и (7.20) полностью определяется напряженно-деформированное состояние основания.

При решении системы (7.27) нужно учитывать следующее. Первое. При задании граничных условий следует помнить, что рассчитываемая область не должна смещаться как жесткое тело. Следовательно, необходимо обеспечить соответствующее закрепление расчетной области. Второе. Чтобы использовать уравнения МКЭ в виде (7.27) граничные данные по перемещениям узлов задают следующим образом. Диагональный элемент общей матрицы жесткости в строке заданного перемещения принимается достаточно большим числом, а элемент в общей матрице узловых сил, соответствующий данному перемещению принимается как произведение этого большого числа на величину заданного перемещения. Граничные значения нагрузок задаются в виде узловых сил, к которым силовые воздействия приближенно приводятся.

В заключение еще раз обратим внимание на то, что в рамках МКЭ непосредственно можно учесть произвольную конфигурацию расчетной области и неоднородность грунтового массива, можно учесть практически все специфические свойства грунтов, а также любые силовые воздействия. Кроме того, в рамках МКЭ можно учесть временное развитие деформаций, как в отношении ползучести грунтов, так и вследствие развития процессов консолидации водонасыщенных пород.

Литература

 

1. Баркан Д.Д. Динамика оснований и фундаментов. М., 1948.

2. Безухов Н.И. Основы теории упругости, пластичности и ползучести.

3. Березанцев В.Г. Расчет оснований сооружений. Л.: Стройиздат, 1970.

4. Бугров А.К., Нарбут Р.М., Сипидин В.П. Исследования грунтов в условиях трехосного сжатия. Л., 1987.

5. Вялов С.С. Реологические основы механики грунтов. М., 1862.

6. Герсеванов Н.М. Основы динамики грунтовых масс

7. Гольдин А.Л., Рассказов Л.Н. Проектирование грунтовых плотин, М.: Энергоатомиздат, 1987. 304 с.

8. Гольдштейн М.Н. Механические свойства грунтов. М., 1973.

9. Гольдштейн М.Н., Царьков А.А., Черкасов И.И. Механика грунтов, основания и фундаменты. М.: Транспорт, 1981.

10.Горбунов-Посадов М.И., Маликова Т.А. Расчет конструкций на упругом основании. М., 1973.

11.ГОСТ 25100-95. Грунты. Классификация.

12.ГОСТ 12248-96. Грунты. Методы лабораторного определения характеристик прочности и деформируемости

13.ГОСТ 5180-84 Грунты. Методы лабораторного определения физических характеристик

14.Далматов Б.И. Механика грунтов, основания и фундаменты. М., 1981.

15.Далматов Б.И., Бронин В.Н., Карлов, Мангушев Р.А., Сахаров А.А., Сотников С.Н., Улицкий В.М., ФадеевА.Б. Основания и фундаменты

16.Зарецкий Ю.И. Теория консолидации грунтов. М, 1967.

17.Иванов П.Л. Грунты и основания гидротехнических сооружений. М, 1985.

18.Ивлев Д.Д. Теория идеальной пластичности

19.Кандауров И.И. Механика зернистых сред и ее применение в строительстве

20.Костэ Ж., Санглера Г. Механика грунтов. М.: Стройиздат, 1981. 456с.

21.Малышев М.В. Прочность грунтов и устойчивость оснований сооружений. М., 1994.

22.Маслов Н.Н. Основы инженерной геологии и механики грунтов. М., 1985.

23.Месчан. Ползучесть глинистых грунтов

24.Ржаницын

25.СНиП 2.02.01-83. Основания зданий и сооружений. М., 1985.

26.СНиП 2.02.04-88. Основания и фундаменты на вечномерзлых грунтах

27.Соколовский В.В. Статика сыпучей среды. М., 1960.

28.Соловьев Г.П.

29.Соловьев Ю И. Плоские задачи механики грунтов. Новосибирск, 1993.

30.Тер-Мартиросян З.Г.,

⇐ Предыдущая78910111213141516

Поделиться:

Воспользуйтесь поиском по сайту: